マーチマッドネス 2025
ロジックパズル
今週の話題であるマーチ・マッドネスの統計に入る前に、いつもの論理パズルの時間です。それでは、どうぞ。
3人のプレイヤーがゲームをします。プレイヤーには見えないように、各プレイヤーに1枚ずつ、計3枚のコインが投げられます。コインの出目に応じて、そのプレイヤーは目隠しをされ、黒または白の帽子が与えられます。その後、目隠しが外され、各プレイヤーは他の2人のプレイヤーの帽子を見ることができますが、自分の帽子は見えません。
各プレイヤーは秘密投票用紙を渡され、帽子の色を記入します。選択肢は黒、白、パスです。実験が成功するには、白または黒に投票したプレイヤー全員が正解する必要があります。しかし、3人全員が「パス」に投票した場合、実験は失敗となります。
プレイヤーには戦略を練る時間が与えられます。75%の確率で勝てる戦略は何でしょうか?
マーチマッドネスアップデート
かつて私はマーチ・マッドネスのプロポジションベットに熱心に賭けていました。典型的な例としては、パシフィック12カンファレンスのチームが合計何試合勝つかを予想するオーバー/アンダーなどが挙げられます。このような賭けのハンディキャップを設定するには、各シードが予想する試合数を知っておくことが役立ちました。
いくつかの賭けは1回戦で決着します。特に、シード13位以上が勝利するかどうかが賭けの焦点となります。今年のカバーズからいくつか例を挙げてみましょう。
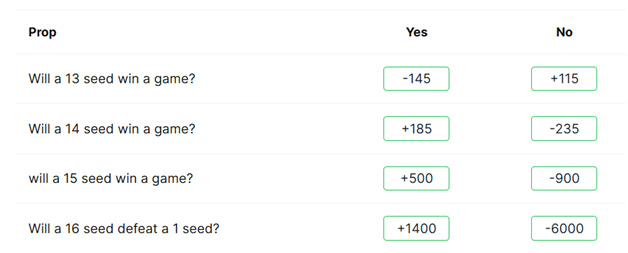
以下の表は、特定のシードが1回戦で勝利する確率と、そのシードの4チームのいずれかが勝利する確率を示しています。これは、1985年から2025年までの40年間のNCAAトーナメントに基づいています。
| シード | 特定のチームの勝利 | どのチームでも第1ラウンドに勝利 |
|---|---|---|
| 1 | 98.75% | 100.00% |
| 2 | 92.50% | 100.00% |
| 3 | 85.63% | 99.96% |
| 4 | 79.38% | 99.82% |
| 5 | 64.38% | 98.39% |
| 6 | 61.25% | 97.75% |
| 7 | 61.25% | 97.75% |
| 8 | 50.00% | 93.75% |
| 9 | 50.00% | 93.75% |
| 10 | 38.75% | 85.93% |
| 11 | 38.75% | 85.93% |
| 12 | 35.63% | 82.83% |
| 13 | 20.63% | 60.31% |
| 14 | 14.38% | 46.25% |
| 15 | 7.50% | 26.79% |
| 16 | 1.25% | 4.91% |
今年の1回戦突破シードの平均は5.34でした。トーナメント全体の平均は5.84です。
第2ラウンドでは、スウィートシックスティーンに進出したチームの平均シード順位は3.44でした。トーナメント平均は4.52です。2試合を勝ち抜いた最低シード順位は10位でした。つまり、今年はアンダードッグチームが最初の2ラウンドで良い成績を残せなかったということです。
第3ラウンドでは、エリートエイトに進出した平均シードは1.625でした。トーナメント平均は3.30です。3試合を勝ち残った最低シードは3試合で、そのうち1試合のみでした。これは、3試合を勝ち残った最低シードのトーナメント記録に並ぶものです。これは2007年と2009年の2回記録に匹敵します。平均シード1.625は、トーナメント史上最低記録です。
ファイナルフォーでは、4チームすべてが1位でした。これは大会史上、2008年の1度だけ起こったことです。ファイナルフォーに進出する1位チームの正確な数を賭ける、人気のプロポジションベットがあります。今年のCoversによるその賭けをご紹介します。
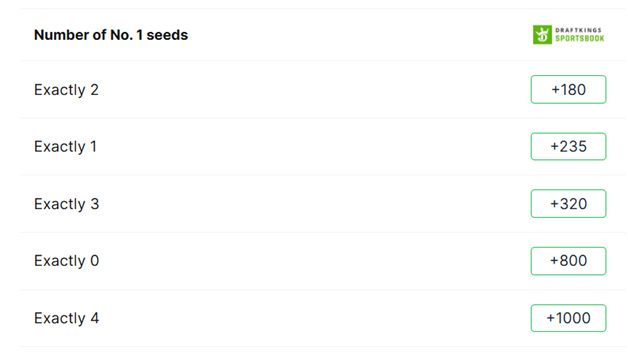
次の表は、40 年間のトーナメントの歴史の中で、第 1 シードのチームがファイナル フォーに何チーム進出したかを示しています。
| #1シード | カウント | 確率 |
|---|---|---|
| 4 | 2 | 5.00% |
| 3 | 4 | 10.00% |
| 2 | 15 | 37.50% |
| 1 | 16 | 40.00% |
| 0 | 3 | 7.50% |
| 合計 | 40 | 100.00% |
特定の第 1 シードのチームがファイナル フォーに進出する確率は 41.25% です。
言うまでもなく、ファイナル フォーの 4 チームはすべて第 1 シードなので、第 1 シードの 2 チームが優勝するだけでなく、チャンピオンシップ ゲームにも出場することになります。
もう一つのプロポジションベットは、チャンピオンシップゲームのシード順です。今年のカバーズベットはこちらです。
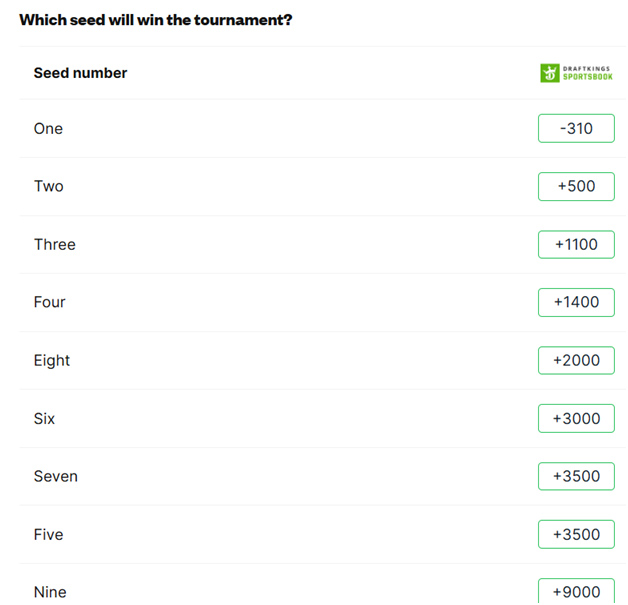
次の表は、各シードがチャンピオンシップ ゲームで優勝した頻度を示しています。
| 勝利シード | カウント | 確率 |
|---|---|---|
| 1 | 26 | 65.00% |
| 2 | 5 | 12.50% |
| 3 | 4 | 10.00% |
| 4 | 2 | 5.00% |
| 5 | 0 | 0.00% |
| 6 | 1 | 2.50% |
| 7 | 1 | 2.50% |
| 8 | 1 | 2.50% |
| 9~16歳 | 0 | 0.00% |
| 合計 | 40 | 100.00% |
シード別の予想勝利数に戻ると、今シーズンのデータを含む最新の表がこちらにあります。
| シード | 平均勝利数 |
|---|---|
| 1 | 3.34 |
| 2 | 2.33 |
| 3 | 1.84 |
| 4 | 1.56 |
| 5 | 1.14 |
| 6 | 1.06 |
| 7 | 0.89 |
| 8 | 0.73 |
| 9 | 0.59 |
| 10 | 0.61 |
| 11 | 0.64 |
| 12 | 0.51 |
| 13 | 0.24 |
| 14 | 0.16 |
| 15 | 0.11 |
| 16 | 0.01 |
よく聞かれる質問の一つは、パーフェクトブラケットの確率です。1対1の状況を除き、常にシードの高い試合(または低い番号の試合)を選ぶ戦略を前提とすると、今シーズンのデータを含めた最新の確率は2億8754万8153分の1になります。
ロジックパズルの答え
戦略は次のようになります。
- • 反対色の帽子が 2 つある場合は、パスします。
- • 同じ色の帽子が 2 つある場合は、反対色を選びます。
3 つの色に応じて、次のような結果が予想されます。
- • 黒3枚:プレイヤー全員が黒2枚を見て白に投票します。全員が間違っているため、実験は失敗します。
- • 黒2つ、白1つ:白のプレイヤーは黒の帽子を2つ見て正しく白に投票します。黒のプレイヤー2人はそれぞれ1つずつ見てパスします。実験は成功です。
- • 黒1つ、白2つ:黒のプレイヤーは白い帽子を2つ見て正しく黒に投票します。白のプレイヤー2人はそれぞれ1つずつ見てパスします。実験は成功です。
- • 白3枚:プレイヤー全員が白2枚を見て黒に投票します。全員が間違っているため、実験は失敗します。
白が3つ、または黒が3つ出る確率は2*(1/2) ³ = 25%です。もう1つの確率は、2色を2対1で分ける場合で、その確率は75%です。上記のように、2対1で分ける場合、実験は成功します。


