ミーン・ガールズの数学問題
先週のニュースレターで、映画『グッド・ウィル・ハンティング』の2つ目の数学問題を紹介したことを覚えている方もいるかもしれません。映画では、MITの数学科が解くのに2年かかったとされています。先週お伝えしたように、この問題は非常に簡単なだけでなく、マット・デイモン演じる数学の天才キャラクターは、解答の80%しか示せませんでした。
今週は、数学の問題が重要なプロットポイントとなっている別の映画を取り上げます。映画は『ミーン・ガールズ』です。高校の数学コンテストで、リンジー・ローハン演じるケイディが次の質問に答えることになります。
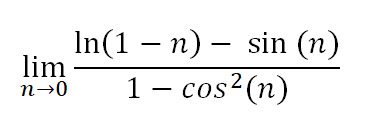
問題のシーンは以下のYouTube動画でご覧いただけます。疑問は4分53秒あたりで提起されています。

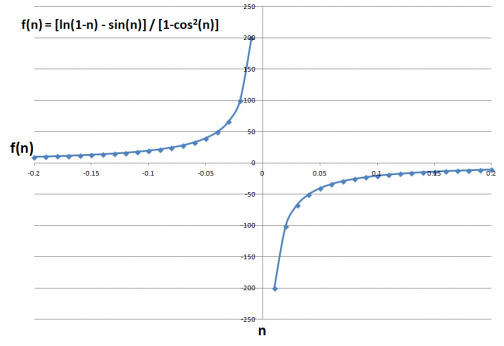
もしスプレッドシートを使えるなら、xが負の側から0に近づくとf(x)は無限大に近づくことが簡単にわかるでしょう。xが正の側から0に近づくと、f(x)は負の無限大に近づきます。つまり、コンピュータの助けを借りれば、関数は負の無限大と正の無限大の両方に近づくため、特に何にも近づいていないことがわかります。したがって、極限は存在しません。
しかし、映画の中ではコンピューターの使用は許可されていませんでした。この問題の解決を助けるために、 ロピタルのルールを思い出してみましょう。
基本的に、f(x)/g(x) = 0/0 の極限であれば、lim f(x)/g(x) = lim f'(x)/g'(x) となる、ということになります。ここでは挙げていないその他の条件については、上記のリンクを参照してください。
「L'Hospital」の「o」の上にサーカムフレックスコームを入れるのを忘れた、なんてメールは送らないでください。どちらの綴りでも大丈夫だと思います。まだ発音がわからないのですが、このニュースレターでは発音しなくて済むのは嬉しいです。
まず、ロピタルの法則の使用が適切な別の問題を投稿します。これは、前にリンクした Wikipedia ページから引用したものです。
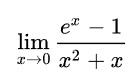
x の極限が 0 に近づくにつれて、分子と分母は両方とも 0 に近づきます。0/0 では何もできません。ロピタルの定理によれば、分子と分母の両方を微分し、その分数の x が 0 に近づくときの極限を求めることができます。さあ、やってみましょう。
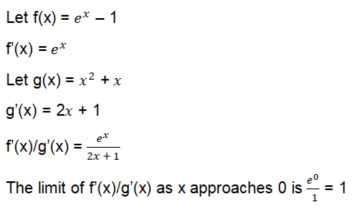
さあ、ロピタルが救助に来ます。
さて、ミーン・ガールズの制限に戻りましょう。
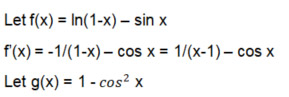
積の法則を使って g(x) を微分してみましょう。(r(x) * s(x))' = r(x)*s'(x) + r'(x)*s(x) であることを思い出してください。
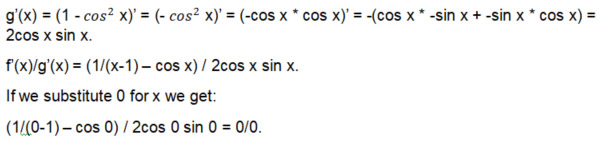
つまり、ロピタルはミーン・ガールズ問題の解決には役立たなかったということです。結局、意味のない0/0のままなので、「限界はない」と言えるでしょう。このシーンでは、ケイディの言う通り、彼女のチームが当然の勝利を収めました。
映画の脚本を担当したティナ・フェイに、数学的な正確さを称賛したいと思います。これは当然のことではありません。『グッド・ウィル・ハンティング』で見たように、どんなに洗練された高予算映画でも、背筋が凍るような数学的・科学的な誤りが潜んでいることがあるのです。


