ピタゴラスの公式の証明
今週は、直角三角形において、辺の平方の和が斜辺の平方に等しいという、古典的なピタゴラスの定理を証明します。最も有名な例は、辺が3、4、5の直角三角形です。3 2 + 4 2 = 5 2であることに注目してください。しかし、その前に、いつもの毎週の論理パズルを出題します。
ロジックパズル
うっかりした古代の哲学者は、家の壁に掛けてある大きな時計の巻き上げを忘れてしまいました。ラジオもテレビも電話もインターネットも、時間を知る手段は何もありませんでした。そこで彼は、まっすぐな砂漠の道を数マイル歩いた友人の家まで歩いて行きました。友人の家に一晩泊まり、家に帰ってきたときには時計の合わせ方を知っていました。どうして分かったのでしょう?
答えはニュースレターの最後にあります。
ピタゴラスの公式の証明
次の図を考えてみましょう。これは、大きな正方形を4つの等しい直角三角形に分割し、中央に小さな正方形を配置したものです。どの三角形の内角の和も180度なので、中央に正方形が1つあることになります。これは2025年11月13日のニュースレターで証明しました。
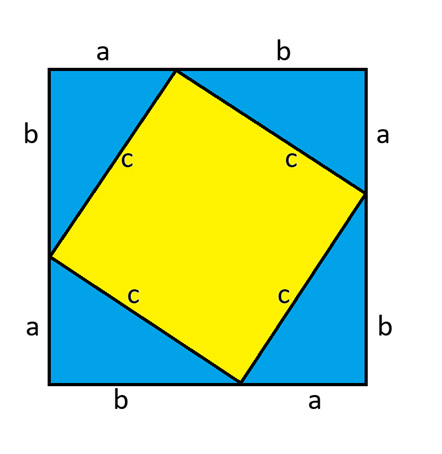
大きな正方形の面積は (a+b) 2です。各三角形の面積はab 2です。中央の黄色い正方形の面積は c 2です。大きな正方形の面積を内部部分の合計と等しくすると、次のようになります。
6; フォントファミリー: 'Open Sans'、サンセリフ; 色: #313131 !important;">(a+b) 2 = 4 ab 2 + c 2
a 2 + 2ab + b 2 = 2ab + c 2
両辺から2abを引くと次のようになります。
a 2 + b 2 = c 2
ロジックパズルの解答
- 教授は時計を巻き、任意の時間に設定した。
- 友達の家に着くと、彼は到着時間をメモします。
- 帰るときには、出発した時間を記録するとともに、出発した時間から到着した時間を引いて友人の家で過ごした時間を計算します。
- 彼は友達の家に行ったときと同じ速さで帰るように気をつけています。
- 彼が家に帰ると、時計は友人の家で過ごした時間と歩いていた時間だけ進んでいるはずです。友人の家で過ごした時間を合計時間から差し引くことで、歩いていた時間を計算できます。そして、合計の歩行時間を2で割ることで、片道の時間を計算できます。
- その後、友人の家を出発した時間と片道の歩行時間を加えた時間を時計に設定できます。
例を見てみましょう。
間違った時計を巻き上げて12時に合わせます。実際の時刻は8時です。彼は友人の家に到着します。1時に家を出て、5時間滞在したと記録します。戻ってみると、時計は8時を指しています。滞在時間の5時間を差し引くと、合計3時間歩いたことになります。つまり、片道1.5時間です。1時に家を出て1.5時間歩いたとすると、今は2時半になっているはずなので、時計をその2時半に合わせます。


