調和級数が発散することの証明

今週の証明は、調和級数が収束することの証明です。しかし、その前に、いつもの論理パズルを出題します。

ロジックパズル

月曜日には、病院の保育室に男の子と女の子の赤ちゃんが二人いました。

火曜日に新しい赤ちゃんが加わります。

水曜日に赤ちゃんがランダムに選ばれます。男の子です。

火曜日に生まれた赤ちゃんが男の子である確率はどれくらいでしょうか?

調和級数が発散することの証明

調和級数はすべての整数の逆数の集合です。言い換えれば、 1 1 、 1 2 、 1 3 、 1 4 、6; font-family: 'Open Sans', sans-serif; color: #313131 !important;"> 1 5 ,…, 1 ∞ 。級数のすべての要素の和が無限大である場合、その級数は発散すると言われています。調和級数の場合は、要素が無限に小さくなるため、これは明らかではありません。しかし、和が確かに無限大であることを証明してみましょう。

方法1：比較テスト

等しいかそれより少ない要素を持つ別の級数が発散することを証明できるなら、調和級数も発散するはずです。

調和級数: 1 1 , 1 2 , 1 3 , 1 4 , 1 5 , 1 6 ,6; フォント ファミリ: 'Open Sans'、sans-serif; 色: #313131 !important;"> 1 7 、 1 8 、 1 9 、 1 10 、 1 11 、 1 12 、 1 13 、…、 1 ∞ 。

シリーズ2: 1 1 , 1 2 ,6; フォントファミリー: 'Open Sans'、サンセリフ; 色: #313131 !important;"> 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 , 1 16 ,6; フォント ファミリ: 'Open Sans'、サンセリフ; 色: #313131 !important;"> 1 16 、 1 16 、 1 16 、 1 32 、…、 1 ∞ 。

数列2は、調和数列と同じ2つの要素から始まります。そして、n>=2ごとに1 2 ⁿ × 2 ^n-1回繰り返されます。数列2のすべての要素は、調和数列の要素と等しいかそれ以下であることに注意してください。数列2は、合計が1 2 ⁿ × 2 ^n-1 = 1 2となるグループに分けることができます。各グループに異なる色を付けて説明しましょう。

シリーズ2: 1 1 ,6; フォントファミリー: 'Open Sans'、サンセリフ; 色: #313131 !important;"> 1 2 , 1 4 , 1 4 , 1 8 , 1 8 , 1 8 , 1 8 , 1 16 , 1 16 , 1 16 ,6; フォントファミリー: 'Open Sans', sans-serif; 色: #00A0D1 !important;"> 1 16 , 1 16 , 1 16 , 1 16 , 1 32 (16 回), 1 64 (32 回) …, 1 ∞

1 + ( 1 2 × ∞) = ∞

方法2：微積分

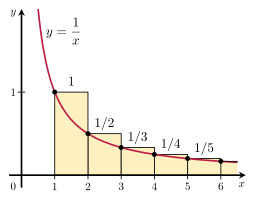
黄色の長方形の面積は、赤い曲線の下の面積よりも大きいことに注意してください。赤い曲線上の面積は次のようになります。

∫ ₁ ^∞ 1 x dx = ln(x) + c 1 から ∞ まで = ln(∞) + c – ln(1) – c = ∞。

ロジックパズルの解答

短い回答

何が起こったのか、2つの説明が考えられます。それぞれXとYと呼びましょう。

X = 火曜日に男の子が追加され、水曜日に男の子が観察された場合。この確率は(1/2)*(2/3) = 2/6 = 1/3です。

Y = 火曜日に女の子が追加され、水曜日に男の子が観察される。この確率は(1/2)*(1/3) = 1/6です。

X+Y = 1/3 + 1/6 = 1/2

問題は、Xが実際に起こった場合の2つの事象の確率を問うものです。つまり、X/(X+Y) = (1/3)/(1/2) = 2/3となります。

長い答え

ベイズの条件付き確率の公式は、Prob(A given B) = Prob(A and B)/Prob(B) となります。ここで、prob(x) は任意の事象 x の確率です。次のように仮定しましょう。

A = 火曜日に追加された男の子

6; フォントファミリー: 'Open Sans'、サンセリフ; 色: #313131 !important; ">B = 水曜日に観察された少年

この場合：

確率(A が B を与えられた場合) = 確率(火曜日に追加された少年が水曜日に観察された少年を与えられた場合) = 確率(火曜日に追加され、水曜日に観察された少年) / 確率(水曜日に観察された少年)。

火曜日の抽選に関する情報がないため、火曜日に男の子が追加された確率は50%です。火曜日に生まれた赤ちゃんが男の子だったと仮定すると、水曜日に生まれた赤ちゃんも男の子である確率は2/3になります。

同様に、火曜日の抽選に関する情報がないため、火曜日に女の子が追加された確率は50%です。火曜日に生まれた赤ちゃんが女の子だったと仮定すると、水曜日に生まれた赤ちゃんが男の子である確率は1/3になります。

水曜日に男の子が抽選される確率は、確率(火曜日に追加された男の子)*確率(水曜日に抽選される男の子) + 確率(火曜日に追加された女の子)*確率(水曜日に抽選される男の子) = (1/2)*(2/3) + (1/2)*(1/3) = 1/2 です。

火曜日に男の子が追加され、水曜日に男の子が抽選される確率 = (1/2)*(2/3) = 1/3。

したがって答えは (1/3)/(1/2) = 2/3 です。