ラウンドロビンスケジューリング
今週のトピックは、ラウンドロビン方式のトーナメントのスケジュール設定方法です。詳しく説明する前に、ラウンドロビンとは、すべてのプレイヤーが他のすべてのプレイヤーと対戦するトーナメント形式です。プレイヤーがn人いるトーナメントでは、試合数はn(n-1)/2となります。
n人のプレイヤー間でn(n-1)/2通りの組み合わせをすべてリストアップするのは簡単です。しかし、理想的には、各プレイヤーが各ラウンドで1回ずつ対戦するラウンドでリストアップします。プレイヤー数が偶数の場合の手順を以下に示します。8人のプレイヤーの場合を例に挙げましょう。次の図では、プレイヤーAからHまでをラベル付けし、4つの四角形の中に対戦する2人のプレイヤーを示しています。これら4つのゲームが第1ラウンドを構成します。全員のプレイ方法に注目してください。
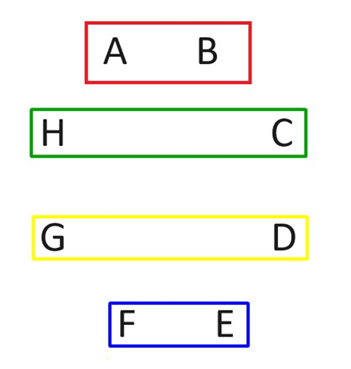
2ラウンド目では、プレイヤーAの位置はそのままに、他のプレイヤー全員を時計回りに回転させます(下図参照)。
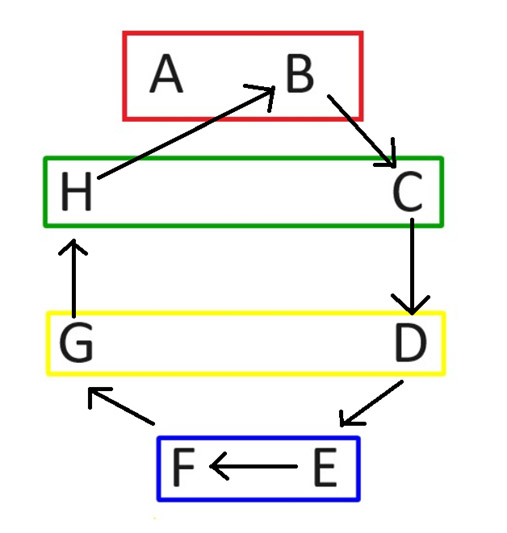
ローテーション後、第 2 ラウンドの試合は次のようになります。
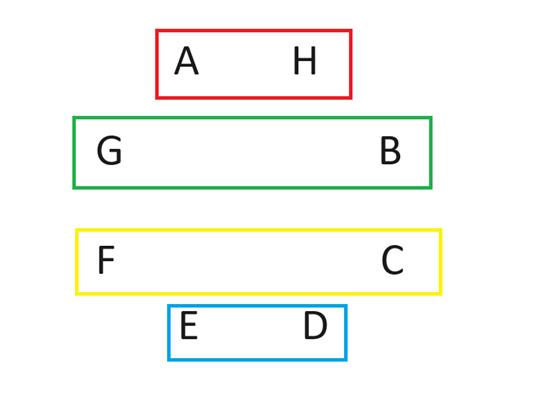
全員がプレイヤーAと対戦するまでこれを繰り返します。なぜこれがうまくいくのかは説明できませんが、とにかくうまくいくのです。プレイヤー数が偶数であれば問題ありません。詳しくは「サークル方式」と「ラウンドロビン」で検索してください。
以下の表は、8人プレイの場合の全対戦を示しています。全員が他のプレイヤーと1回ずつ対戦することに注目してください。
| ラウンド | プレイヤー1 | プレイヤー2 |
|---|---|---|
| 1 | あ | B |
| 1 | H | C |
| 1 | G | D |
| 1 | F | E |
| 1 | あ | H |
| 2 | G | B |
| 2 | F | C |
| 2 | E | D |
| 3 | あ | G |
| 3 | F | H |
| 3 | E | B |
| 3 | D | C |
| 4 | あ | F |
| 4 | E | G |
| 4 | D | H |
| 4 | C | B |
| 5 | あ | E |
| 5 | D | F |
| 5 | C | G |
| 5 | B | H |
| 6 | あ | D |
| 6 | C | E |
| 6 | B | F |
| 6 | H | G |
| 7 | あ | C |
| 7 | B | D |
| 7 | H | E |
| 7 | G | F |
プレイヤー数が奇数の場合は、トーナメントにダミープレイヤーを1人追加するだけで偶数になります。ダミープレイヤーと対戦するプレイヤーは、そのラウンドは不戦勝となり、つまりプレイをスキップします。つまり、全員が1ラウンドは欠席することになります。7人制トーナメントでの例を以下に示します。
| ラウンド | プレイヤー1 | プレイヤー2 |
|---|---|---|
| 1 | あ | B |
| 1 | さよなら | C |
| 1 | G | D |
| 1 | F | E |
| 2 | あ | さよなら |
| 2 | G | B |
| 2 | F | C |
| 2 | E | D |
| 3 | あ | G |
| 3 | F | さよなら |
| 3 | E | B |
| 3 | D | C |
| 4 | あ | F |
| 4 | E | G |
| 4 | D | さよなら |
| 4 | C | B |
| 5 | あ | E |
| 5 | D | F |
| 5 | C | G |
| 5 | B | さよなら |
| 6 | あ | D |
| 6 | C | E |
| 6 | B | F |
| 6 | さよなら | G |
| 7 | あ | C |
| 7 | B | D |
| 7 | さよなら | E |
| 7 | G | F |
最後に、すべてのコートに良い面と悪い面があるテニスのトーナメントを想像してみてください。悪い面はおそらく太陽に面しているでしょう。すべてのプレーヤーが良い面と悪い面を均等に経験できるようにする公平な方法は何でしょうか?
この問題を解決するために、私はビッグバン理論で説明されている「リザード・スポック展開」を提案します。このじゃんけんの遊び方は、奇数個のシンボルでも機能します。どのプレイヤーが良い面を取るかを公平に決定するために、7人プレイヤーの場合を考えてみましょう。次の図は、悪い面を取るプレイヤーを指している矢印で示されているように、どのプレイヤーが良い面を取るかを示しています。
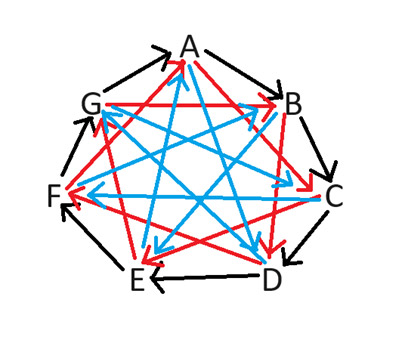
例えば、プレイヤーBとプレイヤーDがプレイした場合、両者の間の矢印がDを指しているため、Bが良い側を獲得します。図の描き方は簡単に理解できます。矢印は常に時計回りです。1から3までのすべての隙間について矢印を描く必要があります。
しかし、このような図を描く必要はなく、文字の輪を描くだけで十分です。円を時計回りに回って、片方のプレイヤーからもう片方のプレイヤーまで移動する両方の方法を考えてみましょう。ステップ数が少ない方が有利な側になります。BとFのゲームを考えてみましょう。時計回りに、Bから4までは4ステップ、FからBまでは3ステップです。3は4より小さいので、Fが有利な側になります。
次の表は、7 人のプレイヤーによる総当たり戦で可能なすべての対戦を、どのプレイヤーが良い側と悪い側を担当するかも含めて示しています。
| ラウンド | 良い面 | 悪い面 |
|---|---|---|
| 1 | あ | B |
| 1 | C | さよなら |
| 1 | D | G |
| 1 | E | F |
| 2 | あ | さよなら |
| 2 | G | B |
| 2 | C | F |
| 2 | D | E |
| 3 | G | あ |
| 3 | F | さよなら |
| 3 | B | E |
| 3 | C | D |
| 4 | F | あ |
| 4 | E | G |
| 4 | D | さよなら |
| 4 | B | C |
| 5 | E | あ |
| 5 | D | F |
| 5 | G | C |
| 5 | B | さよなら |
| 6 | あ | D |
| 6 | C | E |
| 6 | F | B |
| 6 | G | さよなら |
| 7 | あ | C |
| 7 | B | D |
| 7 | E | さよなら |
| 7 | F | G |
残念ながら、このサイドバランス戦略はプレイヤー数が偶数の場合には使用できません。これは、2人のプレイヤーが正反対のサイドにいる場合、サークルの周りの2つの距離が同じになるためです。もし無理やりこの方法を他のマッチアップに適用するのであれば、プレイヤーがサークル上で180度離れている場合、ランダムに選択する必要があります。
今のところ、このトピックについてはここまでです。今後のニュースレターでさらに詳しく取り上げる権利を留保します。今後議論する可能性のあるトピックとしては、3人以上のプレーヤーがいる試合や、各プレーヤーが各コートでプレーする頻度のバランスを取りたい複数のコートの使用などが挙げられます。
最後に、皆様に楽しいハヌカをお祈りします!


