三角形の角度の合計は180度になる定理
三角形の内角の和は180度であることは周知の事実です。今回のニュースレターでは、簡単な証明をご紹介します。ただし、その前に、毎週恒例の論理パズルを出します。
ロジックパズル
王様は49枚の金貨を持っています。それぞれの重さは1グラム、2グラム、3グラム、…49グラムです。7人の息子にそれぞれ7枚の金貨を分け、重さの合計が等しくなるようにするにはどうすればよいでしょうか?
任意の三角形の内角の合計が 180 度になることの証明。
まず、任意の三角形を描き、角度にラベルを付けます。
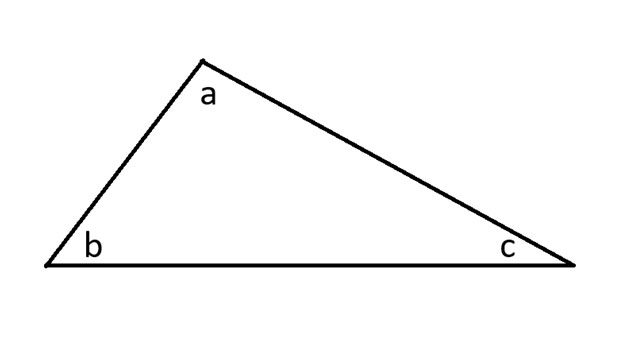
次に、三角形の 3 辺すべてを延長し、角度 a に接する平行線を引きます。
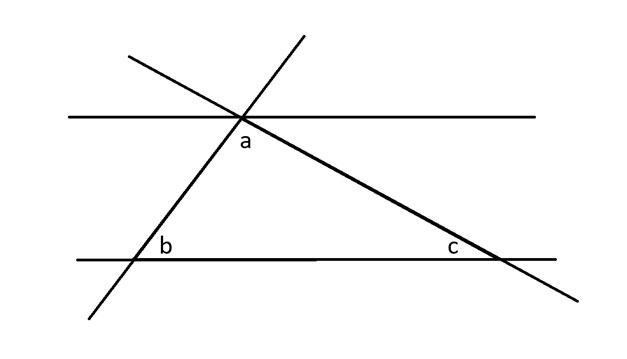
次に、交差する 2 本の線の対角の角度は等しいという対角定理を角度 b に適用します。
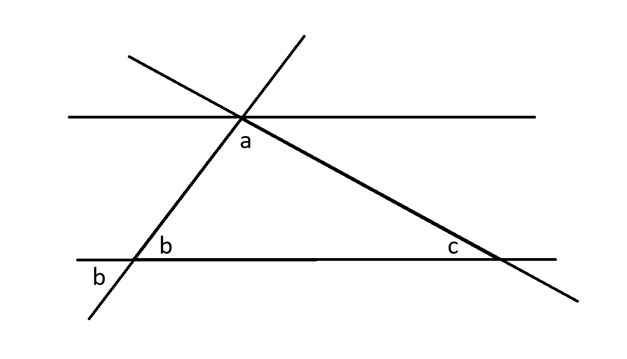
対角線が平行線を横切ると、それぞれの線と交わる部分に同じ角度が生じます。これを応用して、角aの隣にb度の角度を示すことができます。次に、角cについても同じことをします。
6; フォントファミリー: 'Open Sans'、サンセリフ; 色: #313131 !重要; ">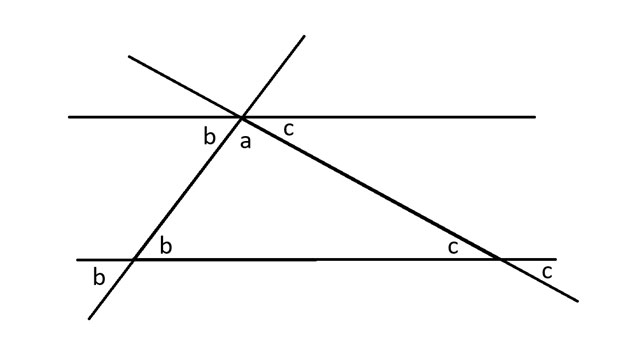
円は360度です。したがって、半円は180度です。言い換えれば、上の平行線の底辺の角度を見ると、a + b + c = 180度となります。これらは元の三角形の3つの角度でもあります。したがって、三角形の角度の合計は180度です。
ロジックパズルの解答
魔方陣を作り、それぞれの息子に1列ずつコインを渡します。行ごとにコインを分けてもいいでしょう。「7×7の魔方陣はどうやって作るの?」と疑問に思うかもしれません。これは「シャム法」として知られ、昔インドで発見されました。
7x7 の戦艦ボードのようなラベルが付いたグリッドから始めましょう。
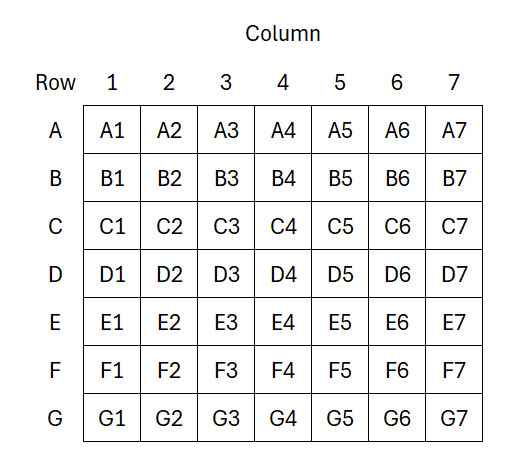
セルA4に1を入力したところから始めます。そして、以下のルールに従ってください。
- 次の配置では、常に前の番号に 1 を加算します。
- そのスペースが占有されているか、すでに A 行または 7 列にいる場合を除き、常に北西方向に進みます。
- 行 A にいる場合は、次の番号を取得するために列 G に進みます。
- 列 7 にいる場合は、次の番号のために列 1 に戻ります。
- 通話 A7 は両方向で G1 にラップアラウンドされます。
- 次に進むべきマスが占有されている場合は、次の数字の次のマス(空いているはずです)まで下がります。
まず始めに:
- セル A4 に 1 があります。
- 行 A にいるため、行 G に折り返して、セル G5 に 2 を入力します。
- 次に、F6 に 3、E7 に 4 を配置します。
- 列 7 にいるので、折り返して、D1 に 5 を入れます。
- C2に6、B3に7を入れます。
- 次に A4 に進みますが、ここには 1 が入っています。そこで、下にスクロールして次の数字である 8 を C3 に置きます。
- 魔方陣がいっぱいになるまで繰り返します。
完成すると次のようになります。
この方法は、奇数次元のあらゆる魔方陣に有効です。
次に、行で分けるか列で分けるかを決めます。それぞれの息子に、いずれかの行/列にあるコインを渡します。例えば、列で分ける場合、息子1は30、38、46、5、13、21、22番目のコインを受け取ります。


