最初のn個の整数の和の証明
今週は、比較的簡単な証明の一つ、1+2+3+…+n = n(n+1)/2 を解説します。2つの非常に直感的な方法で示します。これまでで最も簡単な証明です。しかし、その前に、いつもの毎週の論理パズルを出題します。
ロジックパズル
アリス、ボブ、コールは次のように述べます。
- • アリス:ボブは嘘つきです。
- • ボブ:コールは嘘つきです。
- • コール:アリスとボブは嘘つきです。
三人とも、常に真実を語るか、常に嘘をつくかのどちらかです。他の二人の誠実さは皆知っています。では、真実を語っているのは誰でしょうか?
答えと解決策についてはニュースレターの最後をご覧ください。
最初のn個の整数の和の証明
最初のn個の整数の和はn(n+1)/2であることは誰もが知っているはずです。言い換えれば、1+2+3+…+n = n(n+1)/2です。これが正しい理由を2つの簡単な証明で示します。
方法1
数列の平均値が(n+1)/2であることは簡単に分かります。級数の項数はnです。和は項数と平均項の積、つまりn × (n+1)/2 = n(n+1)/2となります。
同じ方法で、任意の開始点と終了点における和を求めることができます。開始点をa、終了点をbとしましょう。平均は(a+b)/2となり、項の数は(a-b+1)となります。したがって、数列内のすべての数値の合計は (a-b+1) × (a+b)/2 になります。
方法2
次の方法は視覚的に説明する方が簡単です。次の図を見てください。青い四角は1から5までの整数を表しています。
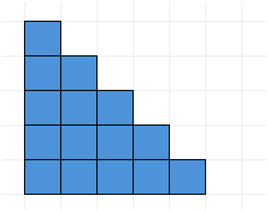
次に、それを複製し、次のように元のピースの横に配置して長方形を作成します。
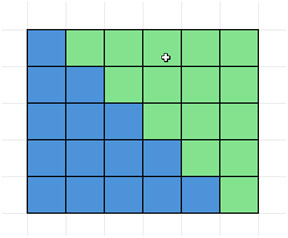
上の長方形の寸法が5×6であることに注目してください。1からnまでの整数を足し合わせる一般的な場合、寸法はn×(n+1)です。そして、この面積を2で割ります。なぜなら、2つのピースのうち片方の面積だけを求めるからです。つまり、片方の面積はn(n+1)/2です。
ロジックパズルの解答
3人とも、真実か嘘かの2つの状態が考えられます。つまり、2 × 3 = 8通りの可能性が考えられます。以下の表にすべて示します。
| シナリオ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| アリス | T | T | T | T | F | F | F | F |
| ボブ | T | T | F | F | T | T | F | F |
| コール | T | F | T | F | T | F | T | F |
ボブとコールは互いを嘘つきと呼んでいることに注目してください。これが可能なのは、どちらかが誠実で、もう一方が嘘つきである場合のみです。したがって、ボブとコールの誠実さが同じである4つの状況は除外できます。残るのはシナリオ2、3、6、7です。これらを一つずつ見ていきましょう。
シナリオ2では、アリスは真実を語っていると仮定します。アリスの真実の発言はボブを嘘つきにします。しかし、このシナリオではボブも真実を語っているため、矛盾が生じます。したがって、シナリオ2は除外されます。
シナリオ3では、アリスは正直であると仮定されています。アリスはボブを嘘つきだと言っていますが、これはシナリオ3の仮定の下では正しいです。しかし、コールは正直者としてリストされており、アリスは嘘をついていると言っています。アリスは同時に正直であり嘘つきであることはできないため、シナリオ3は除外されます。
シナリオ7では、アリスが嘘をついていることが前提となっています。アリスはボブが嘘つきだと言っていますが、これは事実です。しかし、そうするとアリスは正直者になってしまうでしょう。アリスは同時に正直者でありながら嘘つきであるはずがないので、シナリオ7は成立しません。
残るはシナリオ6だけです。これが成り立つか確認してみましょう。もしアリスが嘘つきなら、ボブは正直者になります。もしボブが正直者なら、アリスかボブ、あるいは両方が正直者になります。ボブは正直者なので、コールの発言は偽になります。つまり、この主張は成り立ちます。ボブだけが正直者です。


