ブラックジャックの保険 - ノーと言えばいい!
マイケル・シャックルフォード:皆さん、こんにちは。マイクです。今日のウィザード・オブ・オッズ・アカデミーのレッスンでは、ブラックジャックで絶対にインシュランスをかけてはいけない理由を説明します。インシュランスとは、ディーラーが10ポイントのカードを持っているというサイドベットのことです。
ディーラーが既にエースを表向きにしているときに提供されるため、ディーラーがブラックジャックを出した場合に勝ちとなります。保険の賭け金は、プレイヤーの元の賭け金の半額まで賭けることができ、勝った場合は2倍の配当が支払われます。
私は…するつもりです
…ディーラーが 10 ポイントのカードをホールカードとして持っている場合は、ペースとして 2 を置きます。ディーラーがエースと 9 を持っている場合は、マイナス 1 を置きます。これは、プレーヤーが保険の賭け金を失ったことを表します。
カードを 6 パックと仮定してみましょう。
ディーラーが既に持っているエースアップ以外の情報がないと仮定すると、インシュランスベットで勝てるカードは96枚、つまり残り311枚のうち6枚を16倍した枚数になります。311枚というのは、6デッキのフルシューは312枚で、ディーラーのエースのために1枚を差し引くためです。そして、インシュランスベットが負けになるカードは215枚あります。

勝利と確率の積を取ってみましょう。
2×96÷311は61.74%、215÷311×-1は-69.13%です。つまり、プレイヤーは賭け金の61.74%の勝ちと69.13%の負けを予想できます。合計は-7.40%です。つまり、プレイヤーが保険に賭けた1ドルごとに、7.4セント、つまり保険金額の7.4%の負けを予想できるということです。
7.4%というのはかなり高いハウスアドバンテージなので、インシュランスは絶対にかけないことをお勧めします。コメント欄で「マイク、もしカウントが良かったら?もし私がカードを数えていたとしたら?」と誰かが言う前に、考えてみてください。
はい。もちろん例外もあります。カードを数えていて、残りのカードが10枚以上あると分かっている場合でも、数えていないレクリエーショナルプレイヤーにとっては、保険は最悪の賭けです。繰り返しますが、毎回断ることをお勧めします。
「イーブンマネーはどうですか?」
と疑問に思うかもしれませんね。まずは説明させてください。イーブンマネーオファーとは、インシュランスをかけるのと同じことです。これは、プレイヤーが既にブラックジャックを持っていて、ディーラーがエースを上にしている場合にのみ提供されます。
見てみましょう…
…プレイヤーがブラックジャックを持っていて、インシュランスを取った場合、どちらの場合もどうなるでしょうか。ディーラーがブラックジャックを出した場合、メインベットはプッシュされるため、配当はゼロになりますが、インシュランスベットは1ユニットの配当を得ます。これは、プレイヤーがインシュランスに半額を賭けているためです。インシュランスベットは、ブラックジャックが勝った場合、2倍の配当を得ます。つまり、半額を2倍すると1になります。
次…
ディーラーがブラックジャックを出さなかった場合、プレイヤーのメインベットは1.5ユニットの配当を得られますが、インシュランスベットは0.5ユニットの損失となります。メインベットとインシュランスベットを合わせた配当は、ディーラーがブラックジャックを出した場合は1ユニット、ディーラーがブラックジャックを出さなかった場合は1ユニットとなります。
ディーラーがブラックジャックを持っていても持っていなくても、ディーラーは何も変わりません。プレイヤーがブラックジャックを持っていてインシュランスを取った場合、どちらにしても1ユニットの勝ちとなります。ディーラーが本質的に言っているのは、 「ほら、インシュランスを取れば、私がブラックジャックを持っていても、あなたが1対1で勝つことになる。私が持っているカードを確認する前に、今すぐ支払ってもいいよ」ということです。
魅力的に聞こえますが、実際に試してみる価値があるかどうか、少し計算して考えてみましょう。プレイヤーがブラックジャック、ディーラーがエース、そしてプレイヤーがインシュランスを拒否した状況を考えてみます。ディーラーがホールカードに10を持っている場合、ブラックジャック対ブラックジャックのタイ、つまりプッシュとなるため、プレイヤーは何も勝ちません。ディーラーがホールカードに10以外のカードを持っている場合、プレイヤーは賭け金の3倍、つまり1.5倍の配当を得ます。
仮定してみましょう:
既にテーブル上にあるカード以外に、シューに他のカードがないことを知らない。312枚のシューのうち、残っているカードは309枚で、既に含まれていたカードはプレイヤーのエースと10、そしてディーラーのエースの3枚未満である。
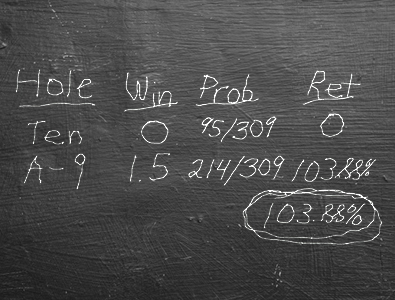
ディーラーがホールカードに10を持っている確率は95÷309です。先ほど言ったように、残りカードは309枚で、シューには10が96枚ありましたが、プレイヤーはそのうち1枚を持っています。ディーラーがホールカードにエースから9を持っている確率は214÷309です。
どちらの方法でもプレイヤーが何を取り戻せるかを見てみましょう。
ディーラーが10をホールカードに持っている場合、0を何に掛ける確率もゼロなので、プレイヤーは何も戻ってこないと予想できます。ディーラーが10をホールカードに持っていない場合、プレイヤーは214÷309の確率で1.5を戻ってくると予想できます。この2つの数字の積は103.88%です。合計しても、同じ103.88%になることは明らかです。
これが意味するのは…
…プレイヤーがブラックジャックで、ディーラーがエースを表向きにしている場合、プレイヤーは賭け金の1.0388倍、つまり約104%の勝利を期待できます。イーブンマネーを選ぶかどうかはプレイヤーの判断です。賭け金の平均103.88%を返してもらえるのか、それとも100%だけなのか?それ以上? 100%か103.88%か? 103.88%の方が高いので、カジノゲームでは必ず期待値を高めるべきですが、イーブンマネーではなく103.88%を目指すべきです。
ここでいくつか注意点があります:
まず1つ目は、プレイヤーがカードを数えておらず、単に娯楽としてプレイしているという前提です。2つ目は、ブラックジャックの配当が3対2であると仮定しています。
最後に、この質問は私のフォーラムで時々出てきて、多くの人が、確かに私は保険金を辞退することについて数学的には良い議論をしているが、心理的な議論はどうなのか、という議論をします。
あなたがブラックジャックでディーラーがエースという状況に陥った場合、イーブンマネーを受け取って確実に勝利を確定させれば 100% の確率で満足できるが、イーブンマネーを拒否すれば満足できる確率は 69.26% しかないと言う人もいるでしょう。
それらの数字は正しいのですが…
…カジノでも現実世界でも、長期的な視点を持つべきです。どんな決断を下すにしても、期待される平均的な利益はどれくらいなのかを考えるべきです。常に保守的にプレイし、小さな勝利を確定させようとしてはいけません。チャンスを掴むことで得られる平均的な利益の方が大きいからです。
もちろん、人生を変えるような状況であれば例外もありますが、ブラックジャックをプレイするということは、そもそもギャンブルが好きであることが前提です。カジノでギャンブルをするのですから、1.5倍の勝利を目指して賭けるべきであり、たった1ドルで妥協してはいけません。さらに、「今すぐ100%幸せになりたいなら、5ドルでも勝ちたい」という理屈を言ったとしても、その幸せは次のハンドまでの1分も続かないのです。
私は思う…
…テーブルを離れ、旅行のために家に帰る時、あなたはどんな幸せを感じているだろうか、と考えてみるべきです。その席や旅行全体で、より多くのお金を勝ち取るか、より少ないお金を失うか、それだけ幸せになれるのです。
さらに、ブラックジャックで勝つチャンスを掴むことで、より多くの、いわばアクションを得られるでしょう。さっきも言ったように、あなたはギャンブルをしているのですから、ギャンブルをしましょう!
この件に関して、他に言うべきことは思いつきません。保険はもちろん、お金に関しても、常に「ノー」と言うように説得できたことを願っています。
ご視聴ありがとうございました。次回のビデオでお会いしましょう。
ルービック キューブ ソルバープログラムを使用して、未解決のルービック キューブの解答を計算します。


