ファイブカードスタッドポーカーの確率
こんにちは、マイクです。このビデオでは、ファイブカードスタッドポーカーの確率の計算方法をご紹介します。言い換えれば、52枚のカードからランダムに5枚を引いた場合、特定のポーカーハンドが形成される確率はどれくらいでしょうか。各ポーカーハンドの組み合わせの数についての質問に答える前に、もう少し簡単な質問をさせていただきます。もし答えが分かっているなら、先に進んでください。
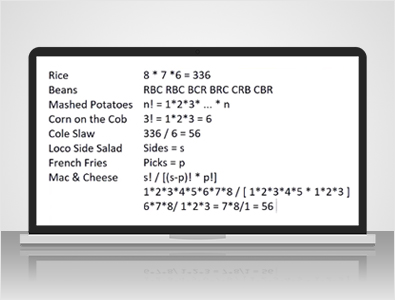
エル・ポヨ・ロコでは:
左にリストしたように、いわゆる定番サイドメニューが8種類あります。デラックスサイドメニューもいくつかありますが、ここでは割愛します。12ピースセットを注文すると、この8種類のサイドメニューの中から3種類を選ぶことができます。仮に3種類とも違うものを選ばなければならないとしましょう。
問題は…
…8種類のサイドメニューのうち、3種類を何通り注文できますか?つまり、毎日お店に行って、毎日3種類のサイドメニューを注文するとします。同じサイドメニューを3つも注文せずに何日過ごせるでしょうか?
もし注文の順番が重要だとしたら、答えは8×7×6になります。なぜなら、最初のものを選ぶ方法は8通り、2番目のものを選ぶ方法は7通り、3番目のものを選ぶ方法は6通りあるからです。しかし、レジ係は気にしません。注文した順番です。
もしあなたが言うなら -
「ライス、豆、コーンがほしい」と言えば、「ライス、豆、コーン」と言っても、「コーン、豆、ライス」と言っても同じ結果になります。では、3種類のサイドメニューを何通りの方法で注文できるでしょうか?例えば、ライス、豆、コーンが好きだとしましょう。その順番で注文することもできますし、ライス、コーン、豆、豆、コーン、ライス、豆、豆、ライス、豆、コーン、ライス、豆、コーン、ライス、豆、ライス、豆、コーン、豆、ライス、つまり6通りの注文方法があります。
書き留めずに、どうして 6 だとわかったのでしょうか?
非常に簡単な公式があります。N個のアイテムがある場合、それらを並べる方法は1 x 2 x 3回、つまりN通りまであります。
この場合の質問は、「3つのものを何通りの順序で並べられるか」です。答えは3です!1 x 2 x 3で、6になります。8つのアイテムを順序に従って並べると、336通りの順序がありますが、それぞれの組み合わせには6通りの順序があるため、6で割ると、残りは56通りになります。
一般的な式は何ですかと疑問に思うかもしれません。
もしあるとしたら、例えば辺の数がSで、選択できる選択肢の数がPだとすると、Sの中からP個のものを選ぶ方法の数を表す一般的な公式はs! / s - p! xp!です。例題を使って、この公式が成り立つことを示しましょう。
この場合:
s = 8 なので、8! は 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 です。分母は s - p、つまり 8 - 3 で、5 または 5! です。つまり、1 x 2 x 3 x 4 x 5 で、p! または 3! なので、1 x 2 x 3 です。1 x 2 x 3 x 4 x 5 は 120 で、分子と分母の両方にあるので、これをキャンセルして、6 x 7 x 8 / 1 x 2 x 3 にします。2 x 3 = 6 で、分子と分母の両方に 6 が出てくるので、これを割ります。
私たちに残されたものはただ...
…7 x 8 / 1 で、56 です。このビデオでは、関数を紹介します。x と y の関数 C を、x から y 個のアイテムを選ぶ方法の数、つまり数学的に言うと x から y 個を選ぶ方法の数と呼び、これを x! / x - y! × y! と定義します。

El Pollo Loco の例では、次のような質問があったとします。
「8 つのスライドのうち 3 つを選択する方法は何通りありますか?」
それをこのように表現すると、スイッチは56になります。さて、いよいよポーカーの話を始められると思います。52枚の中から5枚を選ぶ方法は何通りあるでしょうか?52×5で52!÷47!、つまり52 - 5×5!なので47となり、2,598,960になります。まずはロイヤルフラッシュから始めましょう。
ええ、それはとても簡単です。ロイヤルフラッシュにはハート、スペード、クラブ、ダイヤの4つのスーツがあります。数字は10、ジャック、クイーン、キング、エース。そう、たった4通り。ロイヤルとハート、ダイヤ、クラブ、スペード。
ストレートフラッシュはどうですか?
繰り返しになりますが、ストレートフラッシュの数字は4つのスーツがありますが、最低の数字はエース、つまり2、3、4、5(いわゆるホイール・ストレートフラッシュ)から始まり、9、10、ジャック、クイーン、キングまであります。10、ジャック、クイーン、キング、エースならロイヤルフラッシュになります。最低の数字はエースから9までです。
この場合...
…エースは1として数えます。ストレートフラッシュのスパンは9種類あるので、4スーツ×9スパン=36です。フォー・オブ・ア・カインドの場合、例えばクイーンなど、フォー・オブ・ア・カインドには13通りのランクがあり、フォー・オブ・ア・カインドを構成する4枚のカードを除いたシングルトンカードは48枚残ります。つまり、624になります。
満員御礼
スリーカードには13通りのランクがあり、ペアカードには12通りのランクがあります。スリーカードの場合、4つのスーツから3つを選ぶ3通りの選択肢(チョイス)と、4つのスーツから2つを選ぶ2通りの選択肢(チョイス)を掛け合わせた4通りの選択肢があります。つまり、13 x 12 x 4 x 6で、3,744になります。フラッシュカードの場合、4つのスーツがあります。
与えられたスートの 13 のランクから 5 つを選ぶ方法はいくつありますか?
そうですね、13通りの5の組み合わせですが、そのうち10通りはストレートフラッシュかロイヤルフラッシュになります。例えば、5、6、7、8、9の組み合わせはストレートフラッシュになるので、連続する10通りの数字の組み合わせを選ぶ必要があります。つまり、13通りの5の組み合わせは1,287で、そこから10を引いて4を掛けると5,108になります。
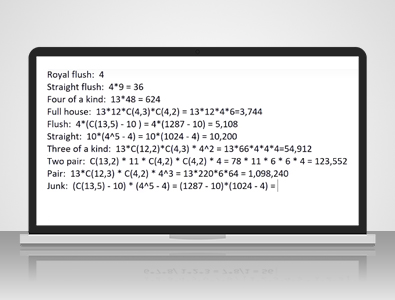
ストレートはいかがですか?
先ほどフラッシュで見たように、ストレートにはエース、2、3、4、5から始まり、10、ジャック、クイーン、キング、エースまで、10通りのスパンがあります。ストレートの各ランクのカードには、それぞれ4つのスーツがあります。4 x 4 x 4 x 4 x 4 = 4^5、つまり5枚のカードそれぞれに異なるスーツを選ぶ方法の数です。5回すべて同じスーツを選んだ場合、ストレートフラッシュまたはロイヤルフラッシュも残ります。これらを差し引く必要があります。4^5 = 1,024 - 4 = 10,200通りのストレートが完成します。
スリー・オブ・ア・カインドはいかがですか?
そうですね、スリーカードのランクの選び方は13通りあります。そして、残りの12通りの中から、2つのシングルトンカードのランクを2つ選ばなければなりません。そして、スリーカードのスートを3つの中から4つ選び、2つのシングルトンカードのそれぞれに4つの中から1つずつ選びます。
スリーカードのランクの選び方は13通りあります。シングルトン2枚の残りの12通りの中から2通りのランクを選ぶ方法は66通りあり、スリーカードの4通りの中から3通りのスーツを選ぶ方法は4通り、シングルトン2枚の1通りのスーツを選ぶ方法も4通りあります。答えは54,912です。
2足はいかがでしょうか?
ええと、ツーペアの場合、13通りのランクから2つを選ぶ「2つ選ぶ」方法が13通りあります。そうすると、シングルトン用に1つのランクが残ります。それぞれのペアについて、4通りのスーツから2つを選ぶ「2つ選ぶ」方法が4通りあります。シングルトンには4つのスーツがあります。13通りの「2つ選ぶ」は78×6×6×4です。シングルトンのランクが11通りだったのを忘れてしまいました。78×11×6×6×4=123,552です。
ペアの場合
ペアのランクは13通りの選び方があり、残りの12通りの中から3つのランクをシングルトン3人のために選びます。ペアの場合、4つのスーツの中から2つを選ぶ方法は4通りあります。そして、3つのシングルトンそれぞれについて、4通りのスーツから選ぶことができます。4 x 4 x 4は、3つのシングルトンのスーツを3つ選ぶ方法の数で、13 x 12です。つまり、12通りの3つを選ぶと、220 x 6 x 4^3 = 64 = 1,098,240になります。
ついに
エースが左上かそれ以下にある確率を計算してみましょう。ここではジャンクと呼びます。ジャンクになるためには、13種類のランクのうち5つの異なるランクが必要です。10種類の中から5種類のランクを選ぶ方法は13通りありますが、フラッシュの時と同じように、ストレートを形成する10番目のスパンを特定する必要があります。5つの連続しないランクを選んだら、それぞれのランクには4つのスーツが考えられます。
4 の 5 乗を取ると...
...ストレートの場合と同じように、毎回同じスーツを選んでフラッシュになる方法の数だけ 4 を減算する必要があります。 5 を選ぶ 13 は 1,287 からストレートの 10 を引くと 4 の 5 乗になり、1,024 から 4 を引くと 1,302,540 になります。
次
これらすべてをスプレッドシートにまとめてみましょう。Excelでどのように計算するか、簡単に説明しましょう。ロイヤルフラッシュは、スーツごとに1つずつ、合計4通り、ストレートフラッシュは36通り、4つのスーツ×9通りのスパンがあることは既に説明しました。フォーカードの場合は、フォーカード4枚とシングルトンカード48枚の合計13通りのランクから選ぶことができます。フルハウスの場合は、スリーカードが13通り、ペアが12通りのランクから選ぶことができます。
スリーカードのスーツを3通り選ぶには、4通りの方法があります。ペアの場合は、4通りの方法から2通りの方法があります。Excelでこの数式を表現するには、先ほど書いたように、大きな数と小さな数を組み合わせた一般的な数式を使います。これで、先ほど得た3,744という数字が得られます。
フラッシュ用
選択できるスーツは4つあり、そのスーツの13段階のうち5段階の数字から、連続するストレートフラッシュまたはロイヤルフラッシュとなる10段階を差し引きます。つまり、フラッシュの数は5,108通りです。ストレートの場合、10段階のスパンがあり、スパン内のカードごとに4つのスーツがありますが、そこからストレートフラッシュまたはロイヤルフラッシュとなる4つのスーツを差し引くと、10,200通りになります。

3種類のもの
スリーカードの場合は13段階、シングルトンの場合は12段階の2段階のランクがあります。4つのスーツの中から3つを選ぶ3通りの方法が4つ、シングルトンの場合は2つのスーツを選ぶ4通りの方法が4つあります。554,912はスリーカードです。ツーペアの場合は、13段階の2段階のランクの中から2つを選ぶ2通りの方法が13つあります。シングルトンの場合は11段階、ツーペアの場合は4つのスーツの中から2つを選ぶ2通りの方法が4つ、シングルトンの場合は4つのスーツの中から2通りの方法が4つあります。
ペアの場合、ランクは13通りあり、シングルトン3人の場合、12通りの中からランクを3つ選ぶ方法は12通りあります。ペアの場合、4つのスーツの中から2つを選ぶ方法は4通りあります。シングルトン3人の場合、3つのスーツを選ぶ方法は4通りあります。
最後に、ジャンク品について
13通りの中から5つのランクを選ぶ5通りの方法は13通りあります。ただし、ストレートになる連続した10通りと、各スーツを選ぶ4通りは除きます。4の5乗からフラッシュになる4通りを引いたものです。ご覧の通り、これらすべてを合計すると2,598,960になります。これはこの動画の冒頭でも示した通りです。さて、実際に応用してみましょう。
私のウェブサイトWizard of Oddsで紹介している何百ものカジノ ゲームのうちの 1 つに、 「Let it ride」というゲームがあります。
そのページを開いてみましょう。これは 5 枚のカードのポーカー ハンドをベースにしたポーカー ゲームです。ドローはなく、すべて 52 枚の中からランダムに選ばれた 5 枚のカードに基づいています。ゲームのルール全体については説明しませんが、5 枚のカードのポーカー バリューに基づいて支払われるサイド ベットがあります。
見えますよ...
…ここには9つの配当表を挙げていますが、表4はかなり一般的なものです。既にこの表に書き写してありますが、賭け金は1ドルです。ロイヤルフラッシュなら2万ドル、ストレートフラッシュなら2万ドル、フォーカードなら400ドルの賞金が得られます。ちなみに、これらの配当は4倍1倍なので、勝っても元の賭け金は戻ってきません。
ここに私がすでに確率を計算したすべての組み合わせがあります。このリターン列は勝利と確率の積です。
たとえば、次のようになります。
先ほども述べたように、ロイヤルフラッシュが出る確率は約400万260万です。この確率を20000倍すると、期待収益は3.08セントになります。これは、プレイヤーが1ドルを賭けた場合、ロイヤルフラッシュの賞金として得られる金額です。ストレートフラッシュなどでは、2.77セントが戻ってくると予想されます。
最終的に計算してみると、プレイヤーは1ドル賭けた場合、74.4667セントの払い戻しを期待できることになります。つまり、1ドル賭けた場合、約74セントの払い戻しが期待できるということです。47% が残り、カジノは 25.53% を保持します。
それを表現する方法は...
…ハウスアドバンテージは25.53%です。少し考えてみてください。カジノは賭け金の25%以上をキープしているのです。これは、サイドベットはどれもくだらない賭けだと私が20年以上言い続けてきたことの証です。この動画から何か一つでも学ぶことがあるとしたら、それが何かだと願っています。この動画はすでに十分長くなりましたが、長くなってしまい申し訳ありません。少しでも参考になり、何かを学ぶことができたなら幸いです。
ご視聴ありがとうございました。


