完璧なブラケットの確率に関するビデオ
こんにちは、マイクです。このビデオでは、 「マーチ マッドネスのブラケットが完璧に埋まる確率はどれくらいか」という質問に答えてみます。
すでに基本的な仕組みについてご存じだと想定しますが、簡単に説明すると、64 のバスケットボール チームがシングル エリミネーション トーナメントで競い合います。つまり、合計 63 試合が行われることになります。
トーナメントは4つのディビジョンに分かれており、各ディビジョンの第1ラウンドでは、第1シードのチームが第16シードのチームと、第2シードのチームが第15シードのチームと、第3シードのチームが第14シードのチームと、といった具合に対戦します。そして、第1ラウンドの全試合の勝者同士が対戦し、第2ラウンドで対戦します。最終的に、勝者が1チームだけになります。
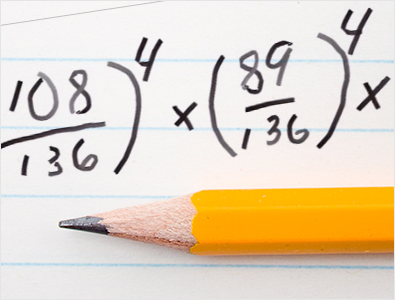
今では毎年3月になると...
メディアでよく取り上げられるのは、完璧なブラケットが埋まる確率です。9京分の1、223京分の1、372京分の1、360京分の1、8億5400万分の1、78万1000分の1という数字を聞くと、背筋がゾッとします。確か。これは単純に、コイントスを63回連続で正しく予想する確率です。マーチマッドネスのブラケットをそんな風に決める人はいないでしょう。なぜなら、チームによって明らかに強いチームと弱いチームがいるからです。例えば、1シードのチームは16シードのチームよりも明らかに強いです。
先に進む前に...
…ちなみに、この動画は2018年4月に撮影されたもので、1985年から2018年までのすべてのマーチマッドネスの試合に基づいています。ところで、 YouTubeでジェフ・バーゲン教授が投稿した別の動画についても触れておきたいと思います。彼は、自分が関わらない戦略を用いると、完璧なブラケットが当たる確率は1280億分の1だと言っています。この数字は、私が得た数字とかなり近いです。
バーゲン教授にその数字をどうやって導き出したのか詳しく説明してもらいたいところですが、ここでは私がどうやってその数字を導き出したのかを詳しく説明します。私の戦略は非常にシンプルです。すべての試合で常に上位のチームを選び、最終的にシード順が4チームだけになった時点でランダムに選ぶというものです。
誰かがコメントを書く前に
現在のゲームのオッズを見ることでこれをさらに改善することができます。たとえば、第 1 シード対第 1 シードの試合になった場合、海外のラスベガスのオッズを見て、基本的にどちらが勝つ可能性が高いかを確認できますが、これについては詳しく説明しません。
この動画では、毎回上位シードのチームを選ぶというシンプルなルールで進めていきます。そして、1位シードの4チームが決まったら、そこからランダムに選びます。さて、導入部分はこれで終わりです。
この動画の次のパートではタブレットを使うことをあらかじめお詫び申し上げます。タブレットをうまく動作させるのに既に多くの技術的な問題を抱えていたため、導入部分をこのように撮影することにしました。それでは早速、先ほど述べた戦略に基づいて、マーチ・マッドネスのパーフェクトブラケットの確率を計算する方法を説明します。
さあ、始めましょう:
これは、クリエイティブペンタブレットを使って作った初めての動画です(そう呼ぶのが適切でしょうか)。ずっとカーンアカデミー風の動画を作りたいと思っていましたが、今回はギャンブルと数学をテーマにしました。前置きはこれくらいにして、早速計算を始めましょう。
1シードが16シードに勝つ確率は、136回中135回と推定します。なぜなら、これまでに136回の試合があり、そのうち135回は1シードが勝っているからです。つまり、1シードが特定の試合で勝つ確率は99.26%です。
しかし...
...4 つの異なる部門があるので、これを 4 回達成する必要があります。つまり、これを 4 乗します。
さて、第2シードが第15シードと対戦する試合が4つあります。136回のうち、第2シードが勝利したのは127回です。過去のデータから判断すると、第2シードが第15シードに勝つ確率は93.38%です。そして、4つの異なるディビジョンで、これを4回繰り返す必要があります。

同様に、第3シードが第14シードに勝つ確率は115÷136で、これも4回計算する必要があります。次に、第4シードが第13シードに勝つ確率は108÷136で、これも4試合勝つ必要があるため、これを4乗する必要があります。
5シードが12シードに勝つ確率は136回中89回で、これは約65.44%の4乗です。6シードが11シードに勝つ確率は136回中85回で、これはどの試合でも62.5%です。7シードが10シードに勝つ確率は136回中83回です。各試合が勝つ確率は61.03%です。最後に、8シードが9シードに勝つ確率は136回中71回で、これも4回に分けて計算する必要があります。
これらのゲームすべてに勝てば...
…1回戦を突破します。そして2回戦では、第1シードのチームが第8シードのチームと対戦します。これはこれまでに72回行われ、そのうち第1シードのチームが第8シードのチームに勝ったのは58回です。第1シードのチームが第8シードのチームに勝つ確率は80.56%で、それでも4回同じ結果になる必要があります。
その後、第4シードのチームが第5シードのチームと対戦します。これはこれまでに73回行われ、そのうち41回は第4シードが勝利しており、各試合の確率は56.16%です。まだ4つのディビジョンがあるので、これを4乗します。
次に、第3シードのチームが第6シードのチームと対戦します。第3シードのチームは70回中41回勝っており、各試合の勝率は58.57%です。最後に、第2ラウンドを突破するために、第2シードのチームは第7シードのチームと対戦します。第2シードのチームは56回勝っており、そのうち79回勝っており、各試合の勝率は70.89%です。さて、これらの試合すべてに勝ったと仮定すると、第3ラウンドに進み、第1シードのチームが第4シードのチームと対戦します。
これまでの大会で、このような対戦は61回発生しており、そのうち44回は第1シードが勝利しており、その確率は毎回72.13%です。その後、第2シードが第3シードと対戦します。これはこれまで52回発生しており、そのうち32回は第2シードが勝利しています。繰り返しますが、これもまだ4回発生する必要があります。
これらすべてのゲームに勝ったと仮定すると:
すると、残るのは第1シードと第2シードの2チームだけになります。過去の試合結果に基づくと、第1シードが第2シードに勝つ確率は64回中35回です。そして、4つのディビジョンで同じことが4回も起こらなければなりません。
さて、ここまで進めば… 4つのディビジョン全てで優勝し、毎回1位チームがトップに立つことになります。ここからランダムにチームを選び始めます。4チームのうち最強のチームを決めるにはあと3試合必要ですが、冒頭で述べたように、ランダムに選ぶだけなので、毎回優勝する確率は2分の1で、あと3試合です。
これが私の戦略を使った場合の勝率で、42,743,890,552分の1ということになります。これでお分かりでしょう。マーチ・マッドネスのブラケットを完璧に埋める上で、これが最も正確な数字だと私は信じています。
冒頭でも述べたように、ベッティング市場の現在のオッズを確認することで、この状況を改善できます。この動画をご覧いただきありがとうございました。あまり良い出来ではなかったことは承知しています。
これは私にとって学びの経験だと捉えてください。繰り返しますが、これはすべて私のウェブサイトwizardofodds.comのスポーツベッティングセクションに書かれています。そして、マーチマッドネスの完璧なブラケットの記入方法についてのページもご覧ください。これ以上言うことはないと思います。
それではご覧いただきありがとうございました。


