シックボー - 確率を計算して勝つ | ビデオ
こんにちは、マイクです。
シックボーというゲームで、オッズの計算方法を学びます。簡単に言うと、シックボーは3つのサイコロを振る非常に古い中国のゲームです。このゲームでは、様々な賭け方から選ぶことができます。

私がこれからやろうとしていること:
フォーラムで動画が長すぎると皆さんから苦情をいただいているため、このトピックを2つの動画に分割することにしました。最初のパートでは、3つのサイコロで3から18までの任意の合計が出る確率と、任意のサイコロの面で0、1、2、または3が出る確率を計算する方法を説明します。
これらの質問に対する答えがわかれば…
…パート 2 に進み、シックボーのさまざまな賭けでどのような価値が得られるのかを分析します。
「6面サイコロを3つ振って、任意の合計が出る確率はどれくらいか?」という質問に答えてみましょう。これから紹介するテクニックは、サイコロの数に関係なく使えます。
このちょっとしたテクニックは、英国サマセットのロバート・グッドハンド氏に教えてもらいました。私の「魔法使いに聞く」コラム264で紹介しているので、ここで皆さんにもシェアしたいと思います。
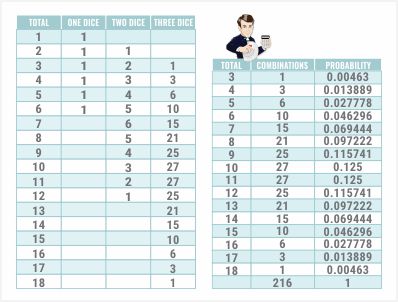
まず、 5つのダミーマスを定義する必要があります。理由はすぐに分かります。では、1から18までの合計をすべてリストアップしてみましょう。サイコロ1個で1、2、6が出る可能性は当然1つしかありません。
それぞれの面には1つの面があるので、分かりやすいでしょう。サイコロを2つ振る場合、左の列(この場合はB列)の合計を求めます。まず左端の1マス目から始めて、その上の5マス目までの合計を求めます。
今回のケースでは…
…セルC8を操作しています。これは、2つのサイコロを振って合計が2になる方法の数を表しています。セルB2からB7までの値を合計しています。セルが空白の場合、Excelはそれをゼロと正しく認識します。
これをコピーして、12までのすべての可能な合計を貼り付けます。合計が2の場合は投げ方が1つ、合計が3の場合は投げ方が2つ、合計が4の場合は投げ方が3つあることがわかります。
さて、なぜこれが機能するのでしょうか?
合計が2になることを考えてみましょう。合計が2になるには、最初のサイコロが1で、2番目のサイコロも1でなければなりません。最初のサイコロが1になる方法は1通りしかなく、当然2番目のサイコロが1になる方法も1通りしかありません。合計が3になる場合、2通りの方法があります。
最初のサイコロが1で2が出る可能性は1通りあり、さらに最初のサイコロが2で2が出る可能性も1通りあります。合計4通りあるので、最初のサイコロは1から3までになります。
合計5つです。
最初のサイコロの合計は1から4でなければなりません。最初のサイコロがその許容範囲内であれば、次のサイコロの合計があなたが言及している値になる可能性が1つあります。
3つのサイコロに進みましょう
全く同じ手法です。同じ数式をコピー&ペーストするだけです。先ほど作成した範囲のどこからでも取得できます。ここでは、1つ右のセルにコピー&ペーストし、さらに下にコピー&ペーストします。これで、3つのサイコロで3から18までの合計を出す組み合わせの数が得られます。
例えば:
合計が3になる方法は1つ、合計が4になる方法は3つ、合計が5になる方法は6つ、などなど。なぜそうなるのでしょうか?また疑問に思うかもしれません。例えば、合計が7の場合を考えてみましょう。サイコロを3つ振って合計が7になるには、サイコロを2つ振って合計が2で、それに5を足せばいいのです。
最初の2つのサイコロの合計が2になる可能性は1つあります。もう1つの可能性は、最初の2つのサイコロの合計が3で、3つ目のサイコロの合計が4になる可能性です。先ほど見たように、最初の2つのサイコロの合計が3になる可能性は2つあり、最初の2つのサイコロの合計が4になる可能性は3つあります。
合計 7 つを取得するには...
…最初の2つのサイコロの合計は2から6でなければなりません。先ほど見たように、その合計は1から5までの合計で15通りになります。これを分かりやすい表にまとめてみましょう。繰り返しますが、これが合計です。
組み合わせは次のとおりです。
合計すると216になります。この数字は見覚えがありますね。もしかしたら、6の3乗かもしれません。
最後に、それぞれの合計の確率を計算してみましょう。
組み合わせの数を合計で割るだけです。30から18までの合計が出る確率があります。次に、特定のサイコロの面が0回から3回出る確率を見てみましょう。シックボーには、サイコロの面ごとに6種類の賭け方があります。
選んだ面が1回出れば1対1、2回出れば2対1、3回出れば3対1の確率で勝ちます。ところで、多くの人が複数の事象について話しているときに、それぞれのサイコロが独立した事象であるかのように、確率を間違って計算してしまいます。
足し算をするのではなく、掛け算をするのです。
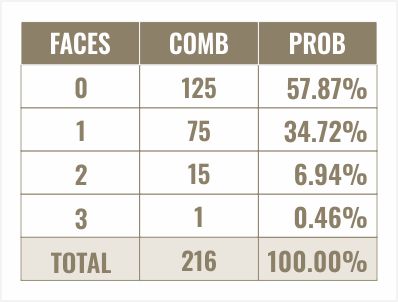
私は物事をまず組み合わせで考えるのが好きです。例えば、6を選んだとします。3つのサイコロで6が3回とも出る組み合わせは何通りあるでしょうか?ええ、単純に1通りです。6-6-6の1通りしかありません。2通りならどうでしょう?
例えば:
6-6-4 または 2-6-6、6-1-6。サイコロのうち2つは6で、もう1つは何か他の目です。何か他の目は他の5つの面のいずれかで、この何か他の目は3つのサイコロのいずれかに現れる可能性があります。選択したサイコロの面が3つのサイコロのうち2つ現れる可能性は合計15通りあります。
一度に表示される方法の数はどのくらいですか?
そうですね、選んだ面以外の残りの2つのサイコロは、5つの面のいずれかになります。5×5なのは、1つは6か選んだ面以外なら何でも出る可能性があり、もう1つも他の5つの面のいずれかになる可能性があるからです。
ついに…
…3倍するのは、選んだ面のサイコロは3つのサイコロのどれか1つになる可能性があるからです。選んだ面を1回振る場合、出目は5×5×3で75通りになります。例えば、6の面を選んだ場合、6-1-2、1-4-6、1-6-5、2-6-2、6-1-3などとなります。
選択したサイコロの面をまったく出さない組み合わせの数はどのくらいでしょうか?
ええと、3つのサイコロはそれぞれ5つの可能性を持っています。5つのサイコロ、つまり3つのサイコロで、選んだ面以外のサイコロそれぞれに5通りの組み合わせがあり、5×5×5、つまり125通りです。これらの組み合わせをすべて合計すると、再び216になります。これも6の3乗なので、何か間違ったことをしたに違いありません。
最後に、確率を見てみましょう
単純に組み合わせの数を合計の組み合わせ数で割ります。これをパーセントで表してみましょう。ここで、選んだ面が0回出る確率は57.87%、1回出る確率は34.72%、2回出る確率は6.94%、3回出る確率は0.46%です。
分かりやすく説明できたでしょうか?パート2では、様々なシックボーのオッズを計算していきますので、ぜひご覧ください。
ご視聴ありがとうございました。
このドキュメントはインスタントHTMLエディタツールで作成されています。こちらをクリックして無料でお試しください。


