Wizardに尋ねる #171
2進数に関しては正しい戦略ですが、必ずしも勝利の戦略とは言えません。まず、相手に1の行を奇数個残せるならそうしましょう。そうでない場合は、各行を2進数の要素に分解します。例えば、99は64+32+2+1です。次に、すべての行の各要素の数を合計します。そして、すべての行で相手にすべての2進数の要素が偶数個残るようなプレイを探します。
例を見てみましょう。次のようなシナリオであなたの番が来たとします。
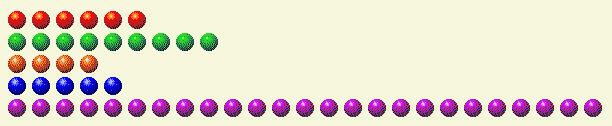
次の表は、各行をバイナリ コンポーネントに分解します。
プレイヤーのターン1
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 25 | 1 | 0 | 0 | 1 | 1 |
| 合計 | 3 | 1 | 3 | 2 | 1 |
1、2、4、16が奇数であることがわかります。16を消すには、25の列を16より小さくする必要があります。2進数の要素の合計を偶数にするには、1を消し、2を足し、4を足し、8を残し、16を消す必要があります。つまり、最善のプレイは最後の列で2+4+8=14となることです。一番下の列に14を残すと、次のようになります。
コンピュータのターン1
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 合計 | 2 | 2 | 4 | 2 | 0 |
コンピューターが順番に処理して、これを私たちに残します。
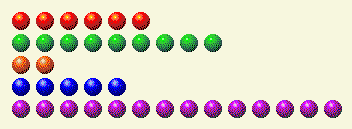
そのバイナリ内訳は次のとおりです。
プレイヤーのターン2
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 合計 | 2 | 3 | 3 | 2 | 0 |
ここで2と4を1つずつ取り除いて合計を均等にする必要があります。両方の要素を含む行は14だけです。そこから6を引いて8にします。
コンピュータのターン2
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 合計 | 2 | 2 | 2 | 2 | 0 |
コンピューターが順番に処理して、これを私たちに残します。
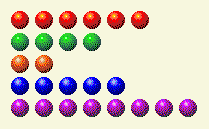
ここで、1、4、8 列を変更する必要があります。
プレイヤーのターン3
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 合計 | 1 | 2 | 3 | 1 | 0 |
それは、次のように 8 行目を 5 行目に変更することで実行できます。
コンピュータのターン3
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 合計 | 2 | 2 | 4 | 0 | 0 |
コンピューターが順番に処理して、これを私たちに残します。
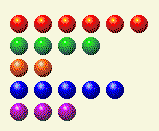
ここで、合計 2 と 4 を変更する必要があります。
プレイヤーのターン4
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 合計 | 2 | 3 | 3 | 0 | 0 |
これは 6 を 0 に変更することで実行できます。
コンピュータのターン4
| 行 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 合計 | 2 | 2 | 2 | 0 | 0 |
コンピューターが順番に処理して、これを私たちに残します。
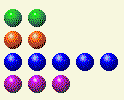
ここで 2 と 4 を変更する必要があります。
プレイヤーのターン5
| 行 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 合計 | 2 | 3 | 1 | 0 | 0 |
これは、5 列を 3 列に変更することで実現できます。相手を x、x、y、y の状況に追い込むことができれば、最後まで同じ状況を維持できれば、必ず勝つことができます。
コンピュータのターン5
| 行 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 合計 | 2 | 4 | 0 | 0 | 0 |
次の数手は、コンピューターをx,x,y,yのパターンに誘導します。ここでコンピューターは2,2,3,2のパターンを残したので、私も2,2,2,2のパターンに誘導します。

するとコンピューターは2、2、1、2と答えます。私は2、2、1、1のままにしておきます。
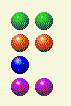
するとコンピューターは2、2、1を残します。私は2、2を残します。もし相手が2列を同じ数にできれば、必ず勝ちます。列を同じ数に保っていれば大丈夫です。

すると、コンピューターは 2 枚のカード 1 組を残し、私は 1 枚を取り除きます。

ここでゲームは終わりです。
オッズが10倍以上の場合、プットベットは良い賭け方だと理解しています。例えば、ポイントが6か8なら、5ドルに加えて50ドルのフリーオッズを賭ける、ということですね。では、なぜポイントを待つ必要があるのでしょうか?パスラインに賭けて、ポイントが6か8ならオッズの10倍全額を賭けたらどうでしょうか?そうすれば、オッズのメリットに加え、7か11が出た場合のメリットも得られるはずです。何か見落としているでしょうか?
同感です。プットベットやプレースベットはお勧めしません。おっしゃる通り、ラインベットをして最大オッズに賭けた方がオッズが良いからです。しかし、どうしてもポイントに直接賭けなければならないという人もいます。もしそうなら、プレース、バイ、プットの中からベストベットを選ぶことをお勧めします。これについては、クラップスのセクションで詳しく説明しています。
友人とラスベガスでプレイしていた時のことです。2デッキゲームで、プレイヤーの合計が10でディーラーが7の時にダブルダウンするのと、プレイヤーの合計が11でディーラーが10の時にダブルダウンするのと、どちらが統計的にオッズが高いかで大喧嘩しました。私は前者だと思っていました。
私のブラックジャック付録9は、まさにこのような疑問に応えるために作成されました。6デッキを想定した場合、私の表によると、8+2を7に対してダブルする期待値は0.396342です。8+3を10に対してダブルする期待値は0.176919です。つまり、おっしゃる通り、10対7の方がはるかに良い手札と言えるでしょう。
あなたのサイトは素晴らしいです。本当にたくさんのことを学びました。ホールデムポーカーのフロップで、20枚のカードで勝ちハンドが完成します。リバーまでにハンドが完成する確率が86%(20/47 + 20/46)ではなく67.5%なのはなぜでしょうか?いろいろ調べてみましたが、とても初歩的なことなのは分かっているのですが、どうしても理解できません。教えていただけると嬉しいです。ありがとうございます!
ありがとうございます!あなたのやり方は、必要な20枚のカードのうち2枚を二重に数えています。ターンで必要な20枚のうち1枚が手に入る確率は20/47 = 0.4255です。ターンで手に入っていなくてリバーで手に入る確率は(27/47)*(20/46) = 0.2498です。つまり、合計確率は0.4255 + 0.2498 = 0.6753です。
私は最近クラップステーブルでのプロトコルを含む地元のカジノにて不思議に思うことがあり、あなたが私のためにそれを明確にしてくれるかどうかを疑問に思います。彼の出てきたロールで「A」は数字を投げてポイントを確立しました。次のロールでは「A」の隣のプレイヤー(プレイヤー「B」)がサイコロを拾って撃ちました。彼がなぜこれをしたのか、あるいは彼が「A」を知っていたのかどうかは明らかではありませんが、他のプレイヤーの1人は「B」が元のシューティングゲームではないと指摘して反対しました。ディーラーとボックスマンによる多くの議論とやり取りの後に、サイコロはハンドを終えた次のプレイヤー(プレイヤー「C」)に渡されました(彼は最終的にセブンアウトになりました)。
これはこの状況下においては適したプロトコルでしたか?もしそうなら、その背後にある戦略は何ですか?プレイヤー「A」が何らかの理由でこれ以上撃ちたくない場合、なぜ彼はサイコロを手放すことを許可されるべきではないのですか?プレイヤー「B」がゲームを理解していなかったためにサイコロを拾った場合、またはスティックマンが誤ってサイコロを彼の前に置いた場合でも、サイコロは「A」に戻ってハンドを終了するべきではありませんか?
nextshooter.com のBone Manにこの件について尋ねました。以下が彼の返信です。
正しいシューター以外のプレイヤーがサイコロを拾って転がした場合、通常それはノーコールかつノーロールであり、サイコロは正しいシューターに戻されるべきです。これは確かに適切な裁定ですが、結果がすべてまたはほとんどのプレイヤーに有利な場合、ボックスマンは場合によってはロールを許可することがあります。場合によっては、ロールの結果がプレイヤーの賭けに影響を与えないことがあります。また、どのプレイヤーもサイコロを次のシューターに送ってハンドを終了するように要求できるので、このような場合では同じサイコロが送られるか、新しいシューターが新しいサイコロを要求することができます。ロールが完了すると、同じシューターは彼/彼女自身の手を撃つことができ、それによって複数の手を持つことができます。
サイコロを20個振ったとき、合計が100を超える確率はどれくらいでしょうか?よろしくお願いします。
これを解くために正規近似法を使い始めましたが、100点を超える確率が低すぎるため、この方法は正確とは言えませんでした。そこで、825万回のランダムシミュレーションを行ったところ、101点以上の試行回数は127回でした。つまり、確率は約65,000分の1です。
さあ、また「ディール・オア・ノー・ディール」の質問の時間です。銀行員による全ての取引とセリーヌ・ディオンのゲスト出演の後、50万ドルと100万ドルのスーツケースが2つ残ったとしましょう。銀行員の提示額はおそらく75万ドルより少し少ないでしょう。どちらを選びますか?もし残った2つのブリーフケースが0.01ドルと100万ドルだったらどうしますか?これはギャンブラーかどうかの問題で、オッズとは関係ないと思います。なぜ質問するかというと、100万ドルを当てられる人がいるのか(たとえ魔法のブリーフケースを選んだとしても)疑問に思うからです。
賞金が人生を変えるほどの額になった場合、賢明なプレイヤーは期待値の最大化を犠牲にして保守的にプレイするべきです。良い戦略とは、期待される幸福度を最大化することです。幸福度を測る良い関数は、総資産の対数だと私は考えています。例えば、10万ドルの資産を持つ人が、0.01ドルと100万ドルの2つのケースを提示されたとします。「ノーディール」を選択した場合の期待幸福度は、0.5*log(100,000.01ドル) + 0.5*log(1,100,000ドル) = 5.520696です。bを、プレイヤーが受け取ることに無関心な銀行のオファーとします。
log(b) = 5.520696
b = 10 5.520696
b = 331,662.50ドル。
したがって、この仮想プレイヤーは銀行が提示する331,662.50ドルには無関心であるはずです。ゲーム開始時の資産が少ないほど、より保守的にプレイするべきです。通常、ゲーム終盤では銀行の提示額は期待値に近くなりますが、場合によっては少し多くなることもあります。プレイヤーが100万ドルを獲得できる合理的なケースは、ゲーム開始時に多額の資産を保有していた場合、または銀行の提示額が異常にケチだった場合のみです。プロデューサーは勤勉な中流階級の人々を好むようなので、多額の金額が絡むゲームで軽率な行動をとるような人物はまず見当たりません。また、ゲーム終盤で銀行が期待値の90%を下回る提示額を提示するのを見たことはありません。100万ドルを獲得する人物が見られるのは、止まらないギャンブラーが番組に出演したときでしょう。そうなったら、私は銀行側を応援するでしょう。
このサイト、大好きです!ラスベガスのブラックジャックのテーブルとそのエッジの詳細なリストを偶然見つけたので、ちょっと疑問に思ったのですが、ブラックジャックのテーブルが2つあって、1つはエッジが0.2%でテーブルミニマムが$10、もう1つはエッジが0.4%でテーブルミニマムが$5だとします。どちらのテーブルも1ハンドあたりの損失は同じ$0.02です。どちらかのテーブルを選ぶことに、何かメリットはあるのでしょうか?
ありがとうございます。この質問に答えるには、まず自分自身になぜギャンブルをするのかを問いかける必要があります。できるだけ損失を抑えたいのであれば、そもそもプレイすべきではありません。しかし、ギャンブルを楽しむためにプレイするのであれば、0.2%のエッジがある10ドルのゲームを選ぶことをお勧めします。予想される損失は同じですが、賭け金が大きければ、より大きな利益が得られます。
カジノ・ナイアガラには、固定オッズではなくジャックポットから配当が支払われるパイゴウポーカーのサイドベットがあります。ジャックポットの配当を最大化するためにハンドをセットした場合、このベットが損益ゼロになるには、ジャックポットの金額がどれくらいになる必要があるのか知りたいです。
損益分岐点は$102,680.24です。この賭けの分析を、パイゴウポーカーのサイドベットのセクションに追加しました。
ポーカーについてはあまり詳しくないのですが、楽しいので、何か教えていただけるとうれしいです。最近妻とラスベガスへ旅行した際、アリゾナ チャーリーズ ディケーターに宿泊しました。ここに宿泊した理由は、ホテルのウェブサイトで $2-$4 ホールデムの広告が出ていたからです。初日の朝、ポーカー ルームへ行き、$2-$4 に名前を記入しました。すると、ポーカー プレーヤーが $4-$8 の欄の下に私たちの名前を書いているのに気づきました。そこで、$2-$4 にしたいと伝えました (同じシートに「$2-$4」という欄がありました)。彼は、$2-$4: フロップ前は $2、フロップ後は $4、ターンとリバー後は $8 だと言いました。私は、$2-$4: フロップ前とフロップ後は $2、ターンとリバー後は $4 という意味だと説明しました。彼は、私たちが何を言っているのかわかっていないかのように笑い、そんなゲームはやらないと言いました。結局、残りの旅行はゴールドコーストでポーカーをしました。ポーカールームではこのような賭け方は普通なのでしょうか?(ポーカールームのスーパーバイザーに、$4-$8ホールデムをプレイできる余裕があるなら、アリゾナ・チャーリーズには泊まらないと伝えてしまいました。)
「2/4」ゲームとは、ターン前はベットが$2単位、ターン後は$4単位であるという意味であることは同意します。しかし、スモールブラインドはおそらく$1でしょう。アリゾナ・チャーリーズがゲームを「2/4」と呼んでいるのはブラインドを指しているように聞こえます。つまり、スモールブラインドは$2、ビッグブラインドは$4で、ターン後は$8ベットすることになります。このような使い方は初めて聞いたので、驚かれるのも無理はありません。
追伸:その後、ポーカー ルームのスーパーバイザーであるアンソニーから次のメッセージを受け取りました。
ポーカールームのスーパーバイザーです。テキサスホールデムのポーカーリミットの正しい表記についてお知らせしたくご連絡いたしました。ゲームが$2/4と表記されている場合、これはベットを指しています(ノーリミットの場合はブラインドのみで表記されます)。プリフロップとポストフロップは$2、ターンとリバーは$4です。$2/$4/$8と表記されているゲーム(前の投稿者が実際に言及していたのはまさにこれだと思います)は、プリフロップは$2、ポストフロップは$4、ターンとリバーは$8です。また、$2/$4/$6/$8と表記されているゲームもあります。参考までにお伝えしておきますが、優れたポーカースーパーバイザーは、プレイヤーにできるだけ多くの情報を提供したいと考えています。


