Wizardに尋ねる #265
保険数理計算ツールを試してみました。私の予想死亡年齢に達する確率が50%未満なのはなぜですか?
平均値と中央値を混同していますね。私の状況を例に考えてみましょう。私は45歳の男性です。平均寿命は78.11歳ですが、80歳まで生きる確率は50.04%です。
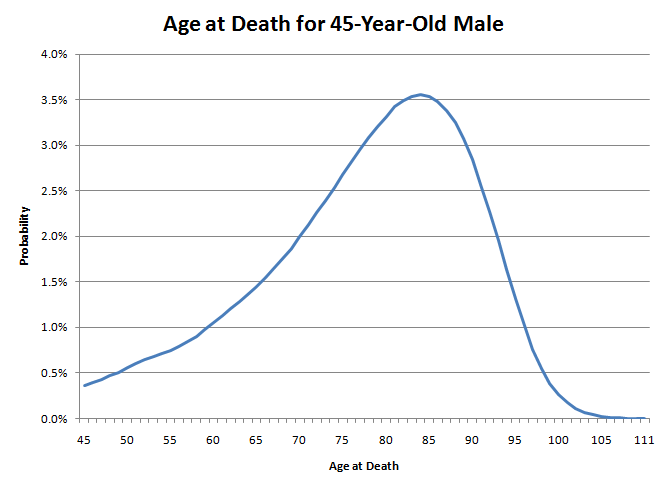
私が死ぬ年齢は、このグラフにダーツを投げるようなものです。左の裾が右よりもずっと太いことに注目してください。これは、現時点での私の死亡確率が非常に低いことを意味します。しかし、年齢を重ねるにつれて、来年の死亡確率は高くなっていきます。たとえば、45歳の男性の場合、46歳まで生き残る確率は99.64%とかなり高くなります。しかし、85歳になると、86歳まで生きられる確率はわずか89.21%になります。これは、自然が背中にゆっくりとナイフを突き刺すようなものです。最初はおそらく死なないでしょうが、年を経るごとに、死ぬ確率はゆっくりと高まります。しかし、70代後半になると、自然はもういい加減にして、本当にナイフを押し込み始めます。
つまり、45歳の男性が多数このグラフにダーツを投げた場合、49.96%が45歳から79歳の間に、50.04%が80歳から111歳の間にダーツを投げることになります。しかし、グラフの右側にたどり着く幸運な半分の男性は、おそらく80歳を超えて長く生きることはないでしょう。男性は80歳に達すると、あと7.78年しか生きられないと予想されます。一方、80歳まで生きられない不運な半分の多くは、それよりもはるかに若くして亡くなります。つまり、平均寿命を縮めているのは、若死が多いことです。
同様の状況として、10、20、30、31、32、33 の番号がついたサイコロを考えてみましょう。平均は 26 ですが、それ以上の目が出る可能性は 2/3 あります。
平均値と中央値の違いを示す例として、サンプルにさらに2人の死亡者を追加したとします。1人は46歳、もう1人は81歳です。80歳まで生きる確率は変わりませんが、45歳時点での平均寿命は短くなります。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
なぜカジノハウスのパイゴウポーカーのルールでは、5枚のエースをキングのペアに分割するという例外規定を設けているのでしょうか?そのようなケースはどのくらいの頻度で発生するのでしょうか?また、発生した場合、その例外規定が影響する確率はどれくらいでしょうか?
いい質問ですね。ハウスウェイでは、5枚のエースを分割し、ローハンドで2枚のエースをプレイします。例外として、ローハンドで2枚のキングをプレイできる場合は、ハイハンドで5枚の同じカードを保持します。私のパイゴウポーカーのページには、ラスベガスとアトランティックシティの7つのハウスウェイが掲載されていますが、すべてこの例外を含んでいます。それ以外の都市の3つには含まれていません。
エース4枚、ジョーカー1枚、キング2枚が出る確率は25,690,513分の1です。ディーラーがバンキングをしている場合、この例外が有効なのは、プレイヤーがハイハンドでフォー・オブ・ア・カインド以上のカードを持っている場合のみです。その確率は約300分の1です。両方が出る確率は約76億分の1です。
ネバダ州ゲーミング管理委員会によると、2009年、ネバダ州には306台のパイゴウポーカーテーブルがありました。1時間あたり60ハンド、テーブルあたり2人のプレイヤー、すべてのテーブルが24時間年中無休で営業していると仮定すると、この例外が発生して結果に変化が生じるまでには23.7年かかります。
つまり、カジノはパイゴウポーカーのディーラー全員に、この例外を暗記させているわけですが、この例外がゲームの歴史上、結果に変化をもたらしたことは一度もないかもしれません。このルールの追加を思いついた人物は、A2345ストレート(通称「ホイール」)を2番目に高いストレートと決めた人物と同じ人物ではないかと私は推測します。
少なくとも 1 つの 12 が出る確率が 50/50 になるには、2 つのサイコロを何回振る必要がありますか。
これは確率論の歴史における古典的な問題です。多くの人が答えは18だと誤解しています。なぜなら、12が出る確率は36分の1で、18×(1/36)=50%だからです。しかし、その論理では、36回振って12が出る確率は100%になりますが、明らかにそうではありません。正しい解は次のとおりです。rを振る回数とします。1回振っても12が出ない確率は35/36です。r回振って12が0個ある確率は(35/36) rです。したがって、次の式でrについて解く必要があります。
(35/36) r = 0.5
log(35/36) r = log(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
r = 24.6051
つまり、丸められた答えはありません。24回振って12が出る確率は1-(35/36) 24 = 49.14%です。25回振って12が出る確率は1-(35/36) 25 = 50.55%です。
これに賭けるなら、例えば25回投げて12が出せるか、誰かが24回投げて12が出せないか、どちらにしても、イーブンマネーで有利になります。
ラスベガスのスポーツブックが、大学フットボールの合計オッズが明らかに間違っていました。マーケットのオッズは43でしたが、ブックメーカーは53で提示していました。そこで、注目を集めたり、オッズが変動したりしないように、少額ずつアンダーに20回ほど賭けました。予想通り、勝ちました。賭け金を支払いに出すのが不安です。カジノ側が支払いを拒否するのは正当なのでしょうか?
10対1で賭けてもいいと思いますが、事前に少し説明があるかもしれません。私が少し疑問に思うのは、スポーツブックはゲーミング・コントロール・ボード(GAB)の許可を得て、明らかに誤って行われた賭けを取り消すことができるからです。
「ブックメーカーは、会長の事前の書面による承認なしに、一方的に賭けを取り消すことはできない。」――ネバダ州規則22.115
この権利は存在しますが、逸話的な証拠に基づくと、実際に行使されることはほとんどありません。どうなるか教えてください。
追伸:質問者から、特に問題なく支払われたと後で知らされました。
伸ばされていない状態で1kmの長さの、無限に伸縮するゴムバンドを想像してみてください。ゴムバンドは毎秒1kmの速度で伸びます。次に、ゴムバンドの片方の端にアリがいると想像してください。ゴムバンドが伸び始めると、アリは現在の位置から毎秒1cmの速度で反対側の端に向かって移動します。アリは反対側の端にたどり着くことができるでしょうか?もしできるとしたら、それはいつでしょうか?
はい、e 100,000 -1 秒後には解けます。mathproblems.infoの問題 206 に 2 つの解答がありますので、そちらをご覧ください。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。


