Wizardに尋ねる #313
他の読者の皆様へお知らせです。クレオパトラ・キノは通常のキノと同じようにプレイできますが、最後に引かれたボールがプレイヤーの選んだ数字と一致し、かつ勝利した場合、プレイヤーは2倍のマルチプライヤーで12回のフリーゲームを獲得できます。フリーゲームでさらにフリーゲームを獲得することはできません。
ピック数や配当表が指定されていないため、3-10-56-180-1000のピック8配当表を例として使用しましょう。まずはリターンを計算してみましょう。
キノでy個のボールの中からx個のボールを選ぶ方法は、20個の中からx個、60個の中からyx個を選ぶ方法と同じです。Excelで表すと、combin(20,x)*combin(60,yx)となります。さらに、combin(x,y) = x!/(y!*(xy)!) となります。つまり、x! = 1*2*3*...*x となります。
確認はここまでにして、このペイテーブルのリターン表をご覧ください。右の列には、後で必要になる勝利の期待値(平方)が表示されています。
ピック8キノ
| イベント | 支払う | 組み合わせ | 確率 | 戻る | リターン^2 |
|---|---|---|---|---|---|
| 0 | 0 | 2,558,620,845 | 0.088266 | 0.000000 | 0.000000 |
| 1 | 0 | 7,724,138,400 | 0.266464 | 0.000000 | 0.000000 |
| 2 | 0 | 9,512,133,400 | 0.328146 | 0.000000 | 0.000000 |
| 3 | 0 | 6,226,123,680 | 0.214786 | 0.000000 | 0.000000 |
| 4 | 3 | 2,362,591,575 | 0.081504 | 0.244511 | 0.733533 |
| 5 | 10 | 5億3054万6880円 | 0.018303 | 0.183026 | 1.830259 |
| 6 | 56 | 68,605,200 | 0.002367 | 0.132536 | 7.422014 |
| 7 | 180 | 4,651,200 | 0.000160 | 0.028882 | 5.198747 |
| 8 | 1000 | 125,970 | 0.000004 | 0.004346 | 4.345661 |
| 合計 | 28,987,537,150 | 1.000000 | 0.593301 | 19.530214 |
次に、平均ボーナスを計算してみましょう。上の表から、ボーナスを除いた平均勝利金は0.593301であることがわかります。ボーナスでは、プレイヤーは12回の2倍フリースピンを獲得します。したがって、ボーナスからの期待勝利金は2×12×0.593301 = 14.239212となります。
次に、ボーナス当選確率を計算してみましょう。プレイヤーが4つの数字を当てた場合、20番目のボールがそれらの4つの数字のいずれかである確率は4/20です。一般的に、プレイヤーがcを当てた場合、20番目のボールが当選に貢献する確率はc/20です。
ボーナス獲得の確率式は、確率(キャッチ4)*(4/20) + 確率(キャッチ5)*(5/20) + 確率(キャッチ6)*(6/20) + 確率(キャッチ7)*(7/20) + 確率(キャッチ8)*(8/20)です。上記のリターン表から、各勝利の確率が分かります。したがって、ボーナス獲得の確率は以下のとおりです。
0.081504*(4/20) + 0.018303*(5/20) + 0.002367*(6/20) + 0.000160*(7/20) + 0.000004*(8/20) = 0.021644。
ボーナスを獲得する確率と平均ボーナス獲得額から、ボーナスからのリターンは 0.021644 × 14.239212 = 0.308198 と計算できます。
知る必要はありませんが、ゲームの全体的なリターンは、ベースゲームからのリターンとボーナスからのリターンを足したもので、0.593301 + 0.308198 = 0.901498 になります。
さて、実際の分散について見ていきましょう。念のため、分散に関する一般的な公式は次のとおりです。
var(x + y) = var(x) + var(y) + 2*cov(x,y) となります。ここで、var は分散、cov は共分散を表します。このゲームの場合、
総分散 = var(ベースゲーム) + var(ボーナス) + 2*cov(ベースゲームとボーナス)。
分散の基本式はE(x^2) - [E(x)]^2です。言い換えれば、期待勝利数の二乗から期待勝利数の二乗を引いた値です。
では、まずはベースゲームの分散から見ていきましょう。先ほど、最初の表から期待勝利額の二乗値が必要になると言いましたね。最初の表の右下のセルには、期待勝利額の二乗値が19.530214と表示されています。期待勝利額は0.593301であることは既に分かっています。したがって、ベースゲームの分散値は19.530214 - 0.593301 2 = 19.178208となります。
次に、ボーナスの分散を計算してみましょう(すでにボーナスを獲得していると仮定します)。そのためには、以下の点を思い出してください。
var(ax) = a 2 x、ここで a は定数です。
また、n 個のランダム変数 x の分散は nx であることも思い出してください。
ただし、ボーナスゲームの基本勝利数をxとすると、ボーナス全体の分散は2 2 × 12 × xとなります。前述の通り、ボーナスを除いたベースゲーム1回のスピンの分散は19.178208です。したがって、ボーナスが既に当選している場合、ボーナス全体の分散は2 2 × 12 × 19.178208 = 920.554000となります。
しかし、ここで知っておくべきなのは、最初のボールが引かれる前のボーナスの分散であり、ボーナスが全く当たらない可能性も含みます。ボーナスの分散に当選確率を掛け合わせるだけではだめです。代わりに、var(x) = E(x^2) - [E(x)]^2 を思い出してください。これを次のように整理してみましょう。
E(x^2) = var(x) + [E(x)]^2
ボーナスの平均と分散はわかっているので、ボーナスで予想される勝利額の二乗は、920.554000 + 19.178208 2 = 1123.309169 となります。
したがって、最初のボールが抽選される前のボーナスからの勝利の期待二乗は、prob(ボーナス) × E(x^2) = 0.021644 × 1123.309169 = 24.313239 です。
ボーナスからの期待勝利額は、最初のボールが出る前は0.308198と既に計算しました。したがって、最初のボールが出る前のボーナスの全体的な分散は、24.313239 - 0.308198 2 = 24.218253となります。
次のステップは共分散を計算することです。「なぜ基本配当とボーナス配当に相関関係があるのですか?」と疑問に思うかもしれません。ボーナスを発動させるには、最後のボールが配当に貢献している必要があるからです。最後のボールが配当に貢献していると仮定すると、平均配当は増加します。ちなみに、ベイズの条件確率の公式は次のようになります。
P(A が B を与えられた場合) = P(A と B)/P(B)。
最後のボールがヒットだったことを前提に、ベース ゲームのリターン テーブルをやり直してみましょう。
ピック8キノはラストボールヒットを与えられる
| イベント | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| 0 | 0 | - | 0.000000 | 0.000000 |
| 1 | 0 | - | 0.000000 | 0。000000 |
| 2 | 0 | - | 0.000000 | 0.000000 |
| 3 | 0 | - | 0.000000 | 0.000000 |
| 4 | 3 | 4億7,251万8,315 | 0.753119 | 2.259358 |
| 5 | 10 | 1億3263万6720 | 0.211402 | 2.114019 |
| 6 | 56 | 20,581,560 | 0.032804 | 1.837010 |
| 7 | 180 | 1,627,920 | 0.002595 | 0.467036 |
| 8 | 1000 | 50,388 | 0.000080 | 0.080310 |
| 合計 | 627,414,903 | 1.000000 | 6.757734 |
右下のセルは、最後のボールがヒットだったと仮定すると、平均勝利は 6.757734 であることを示しています。
次に、大学の統計学の授業で学んだ次のことを思い出してください。
cov(x,y) = exp(xy) - exp(x)*exp(y) 。
この例では、x = ベースゲームの勝利、y = ボーナスゲームの勝利とします。まずは exp(xy) について考えてみましょう。
Exp(xy) = 確率(ボーナス獲得)*(ボーナス獲得時のベースゲームの平均勝利数)*平均(ボーナス勝利数) + 確率(ボーナス未獲得)*(ボーナス未獲得時のベースゲームの平均勝利数)*平均(ボーナス未獲得時のボーナス勝利数)。平均(ボーナス未獲得時のボーナス勝利数) = 0 と簡単に言えるので、次のように書き直すことができます。
Exp(xy) = prob(ボーナス獲得)*(ボーナス獲得時のベースゲームの平均勝利)*平均(ボーナス勝利) =
0.021644 × 6.757734 × 14.239212 = 2.082719。E(x)とE(y)はすでに解いているので、共分散は次のようになります。
cov(x,y) = exp(xy) - exp(x)*exp(y) = 2.082719 - 0.593301 × 0.308198 = 1.899865。
共分散が関係する場合の分散の全体的な方程式に戻りましょう。
総分散 = var(ベースゲーム) + var(ボーナス) + 2*cov(ベースゲームとボーナス) = 19.178208 + 24.218253 + 2×1.899865 = 47.196191。標準偏差はその平方根で、6.869948となります。
ということで、どうぞ。これは何時間もかかったので、気に入っていただけたら嬉しいです。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
アメリカでは一般的に50%と言われている結婚が離婚に終わる確率は、離婚件数と同時期の結婚件数で計算されていると聞きました。これは本当ですか?この統計の算出方法は妥当だと思いますか?短期間の離婚と長期間の結婚を比較している点に疑問を感じます。
人口と年齢の分布が安定しており、離婚確率が本当に 50% であれば、サンプル数が大きい場合、一定期間内に 2 組の結婚に対して 1 組の離婚が見られることが予想されます。
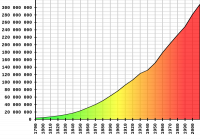
しかし、人口は安定していません。このグラフを見ると、米国の人口は10年ごとに10.71%増加していることがわかります。つまり、年間1.02%です。ここでは単純に1%と仮定しましょう。
地図出典:米国国勢調査
Fatherly.comによれば、失敗した結婚の平均期間は 8 年です。
現在、離婚と結婚の比率が 1 対 2 であるとすると、ある結婚が離婚で終わる平均確率はどれくらいでしょうか。
現在見られる離婚は8年前の結婚によるもので、当時の人口は現在の92.35%でした。単純計算で、実際の離婚確率は54.14%と推定されます。
確認してみましょう。
まず、CDCによると、人口1000人あたり年間6.9組の結婚があるそうです。この数字は今回の質問とは関係ありませんが、関係する数字を理解するのに役立つと思います。
8年前の人口が3億人だったと仮定すると、その年の結婚数は0.69% × 3億 = 207万件となります。
そのうちの 54.14% が 8 年後に離婚に終わるとすると、現在では 2,070,000 * 54.14% = 1,120,698 件の離婚が起こっていることになります。
1,120,698 / 2,070,000 = 現在観測されている結婚数に対する離婚数の比率は 50% です。
誰かに言われないように言っておきますが、すべての離婚がちょうど8年で終わるわけではないことは承知しています。しかし、あらゆることを考慮すると、最終的な離婚率は私の推定する54.14%とそれほど変わらないでしょう。
この質問は、 Wizard of Vegasの私のフォーラムで提起され、議論されています。
100人の従業員がいるオフィスで、シークレットサンタのプレゼント交換をします。全員の名前を紙に書いて帽子に入れ、全員でランダムに名前を引いてプレゼントを贈ります。
問題は、平均していくつの閉じたループが存在するかということです。例えば、ゴードンがドンに渡し、ドンがジョンに渡し、ジョンがネイサンに渡し、ネイサンがゴードンに渡す、といった閉じたループです。あるいは、自分で名前を引く、といった具合です。
全員が一度に一つずつ選択することを考えてみましょう。一人ずつ選択していくと、以下の2つの状況が発生します。
- 選ぶ人の名前はすでに選ばれています。
- 選んだ人の名前はまだ名前の箱の中に残っています。
任意の選択者に対して、選択する人が n 人残っているとします。
選んだ人の名前が既に選ばれている場合、選んだ人が自分の名前を含むループを閉じる確率は1/nです。例えば、エイミーが選んだとします。エイミーの名前は既にボブが、ボブの名前は既にチャーリーが選んでおり、チャーリーの名前はまだビンに残っています。ビンにまだn個の名前が残っている場合、エイミーがチャーリーの名前を選び、ループを閉じる確率は1/nです。
選んだ人の名前がまだ選ばれていない場合、エイミーが自分の名前を選ぶ確率は 1/n で、ループが閉じます。
いずれにせよ、ピッカーがループを閉じない場合、別のチェーンの一部に加わることになり、そのチェーンは最終的に他の誰かによって閉じられます。各チェーンは、閉じられた時点で一度だけカウントされます。
したがって答えは 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518 です。
十分に大きなプレイヤー数 n の場合の推定値は ln(n) です。
この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
ビデオスロットマシンをプレイする場合、追加の保証されたワイルドの価値はどれくらいでしょうか?
それは多くの要因によります。ご質問の意味を解釈すると、プレイヤーが通常獲得する平均数を超える追加ワイルドの価値はどれくらいか、ということです。答えはゲームによって大きく異なりますが、重要な要素は画面上の列数です。列が3つある場合、追加ワイルドはペイラインの1/3に影響します。同様に、列が4つある場合、その価値は低くなり、ペイラインの1/4に影響します。
ご質問にお答えするために、既に分析済みのゲーム「クレオパトラ」を例に挙げてみました。以下の表は、ワイルドの期待値の増加率を、ワイルドの乱数と比較したものです。
クレオパトラにおけるエクストラワイルドの価値
| リール | 3行 | 4行 |
|---|---|---|
| 1 | 95.71% | 71.79% |
| 2 | 99.76% | 74.82% |
| 3 | 76.24% | 57.18% |
| 4 | 21.25% | 15.93% |
| 5 | 1.96% | 1.47% |