Wizardに尋ねる #318
プレイヤーが賞品の価格を全く知らないと仮定して、「プライス・イズ・ライト」のレースゲームをプレイするための最善の戦略は何ですか?
このゲームを知らない読者のために、ビデオを掲載します。
以下の戦略は、平均ターン数が最小となると考えています。これと同等の戦略は数多くありますが、これを上回る戦略はないと思います。
この戦略を使うには、4 つの値札に 1、2、3、4 とラベルを付けます。最初に左から始めて、過去に何回正解したかの履歴に従って、4 つの賞品に値札を付けます。
レースゲーム戦略
| 歴史 | 賞品1 | 賞品2 | 賞品3 | 賞品4 |
|---|---|---|---|---|
| なし | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0,2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
次の表は、4 つの値札を並べる 24 通りの方法のうち、1 ~ 5 ターンかかる確率を示しています。
必要なターン数
| ターン | 番号 | 確率 |
|---|---|---|
| 1 | 1 | 4.17% |
| 2 | 4 | 16.67% |
| 3 | 8 | 33.33% |
| 4 | 9 | 37.50% |
| 5 | 2 | 8.33% |
| 合計 | 24 | 100.00% |
ドット積を取ると、この戦略で必要な平均ターン数は 3.29167 になります。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
2019年9月18日放送のクイズ番組「Jeopardy」には、「カジノゲームを説明しなさい」というカテゴリーがありました。ヒントの一つは「9の数字に合わせて服を着てプレイする。銀行員の勤務時間。ボンドさん、モナコに来た理由は何ですか?」でした。

答えは「バカラ」で、正解と判断されました。ボンドはシャン・ド・フェールをプレイしていたのではないですか?
はい、ボンドはバカラではなく、シュマン・ド・フェールをプレイしていました。主な違いは以下のとおりです。
- バンカーの順番はテーブルを回ります。バンキングプレイヤーは自動的にバンカー*の手札を引き継ぎます。
- プレイヤー* とバンカーはどちらも、2 枚のカードがナチュラル 8 または 9 でない限り、3 枚目のカードを自由に引くことができます。
注記:
いつものように、バカラやシャン・ド・フェールについて書くときは、ゲームをプレイするプレイヤーとの混乱を避けるために、賭けの名前を大文字で書きます。
とはいえ、そのようなシーンが初めて登場するのは、以下の『ドクター・ノオ』のクリップです。このクリップでは、銀行が回転するだけでなく、3枚目のカードではプレイヤーが自由意志を持つだけでなく、動画の2分11秒あたりでボンドが実際にこのゲームを「chemin de fer」と呼んでいます。
次のビデオでは、3 つの異なる映画から 3 つの chemin de fer シーンを紹介します。
各シーンの開始点は次のとおりです。
- 2:09 — サンダーボール作戦
- 4:19 — 女王陛下の007
- 7:30 — ユア・アイズ・オンリー
これら 3 つの映画すべてにおいて、3 枚目のカードの決定におけるプレイヤーの銀行預金と自由意志が見られますが、特に「007 ユア・アイズ・オンリー」ではオッズが議論される場面でそれが顕著です。
最後に、以下は『ゴールデンアイ』のシーンです。
ここでも、バンクへのターンが行ったり来たりし、3枚目のカードを引く際に自由意志が働く様子が見られます。しかし、0:45の時点で女性キャラクターはゲームを「バカラ」と呼んでいます。これは「キャラクターエラー」に分類すべきでしょう。
最後に、ボンドがどの映画でもシュマン・ド・フェールをプレイしていたことは間違いありません。厳密に言えば、審査員が「バカラ」を正解として認めたのは間違いだったと思います。しかし、彼らを責めるつもりはありません。ジェパディの基準から見ても、平均的なプレイヤーにバカラとシュマン・ド・フェールの違いを区別できると期待するのは無理があります。アンソニー・スカラムーチの代わりに「ザ・ムーチ」という答えを認めたことからもわかるように、審査員はより寛容になっているようです。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
映画「ミーン・ガールズ」で問われているように、次の質問とは何ですか?
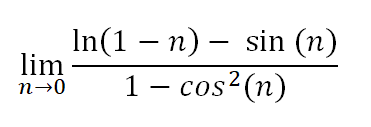
まず、n (x 軸) と f(n) (y 軸) のグラフを見てみましょう。
ご覧の通り、極限は左から∞、右から-∞に近づいていきます。左右から同じ場所には向かないので、極限は存在しません。
しかし、グラフを描かずに質問に答えてみましょう。ロピタルの定理によれば、f(x)/g(x) の極限が 0/0 のとき、lim f(x)/g(x) = lim f'(x)/g'(x) となります。そこで、f'(x) と g'(x) を解きましょう。
f'(n) = ((ln(1-n) - sin(n)) d/dn = -1/(1-n) - cos(n)
g'(n) = (1 - cos 2 (n)) d/dn = sin 2 (n) d/dn
積の法則を使って sin 2 (n) d/dn を解いてみましょう。
sin 2 (n) d/dn = sin(n) × sin(n) d/dn =
sin(n) × cos(n) + cos(n) × sin(n) =
2sin(n)cos(n)。
次に、n = 0 で f'(n) と g'(n) を解きます。
f'(0) = -1/(1-0) - cos(0) = -2 です。
g'(0) = 2sin(0)cos(0) = 0
したがって、f'(0)/g'(0) = -2/0 = -∞ となります。したがって、元の関数の極限は存在しません。

『ミーン・ガールズ』の脚本家たちがこの映画の数学を完璧に描き出したことに賛辞を送りたい。『グッド・ウィル・ハンティング』のような本格的な数学映画でさえ、数学を完全に台無しにしてしまうことがよくある。