Wizardに尋ねる #396
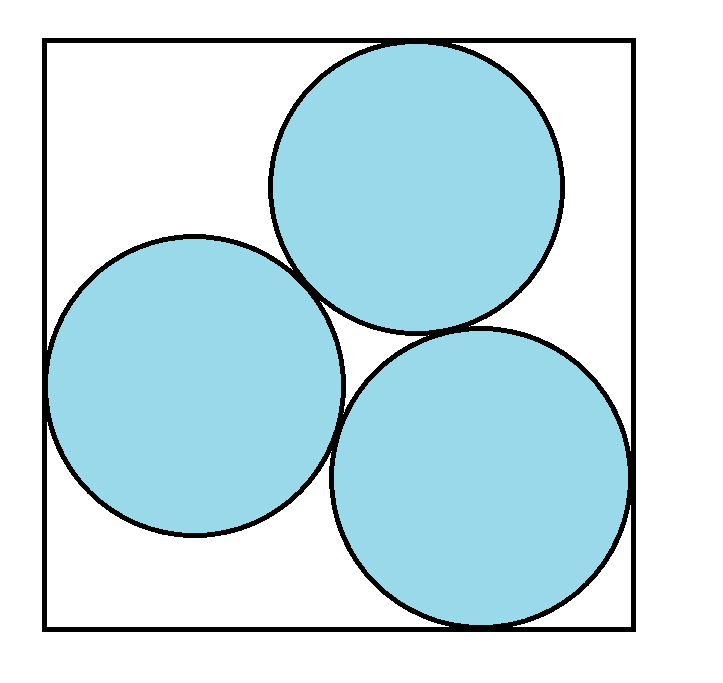
半径1の円が3つ、最小の大きさの正方形に内接しています。正方形の一辺の長さはいくらですか?
これが私の解決策です(PDF)。
映画「ラウンダーズ」でKGBが語ったことは何ですか?
強い手札が出た時は、彼は棚に置いてあるオレオから一枚取りました。どちらにしても、クッキーを一枚ひねって剥がしました。強い手札が出たら食べ、出なかったらトレイに戻しました。
このシーンでは、KGB は最高のフルハウスを持っており、オレオを食べます。
このシーンでは、KGBは明らかにストレートを持っていて、状況的に非常に強いハンドを持っており、オレオを食べています。正直なところ、マイクがなぜ自分のカードをさらけ出し、テルを知っていると発言したのか理解できません。
このシーンでは、KGBが明らかにブラフをかけた。マイクはオールインし、KGBはフォールドする。その後、クッキーを手に取るが食べないことから、ブラフだったことが窺える。
年間の勝敗表によると、2023年のビデオポーカーでの「コインイン」は$1,920,197.60でした。これはすべて$0.25の9-5ダブルダブルボーナス5プレイでした。「コインアウト」とジャックポットを合わせると$1,835,483.75になりました。つまり、損失は$84,713.83です。こんなに運が悪い確率はどれくらいなのでしょうか?
$0.25の5プレイの合計ベット額は$6.25です。ベット回数は$1,920,197.60 / $6.25 = 307,232回です。
1回のベットあたりの分散は306.11です。すべての賭け金の合計分散は306.11 × 307,232 = $94,045,252です。1標準偏差はsqrt($94,045,252) = $9,698です。
9-5ダブルダブルボーナスの期待リターンは、完璧なプレイを前提とすると0.978729です。ハウスエッジによる期待損失は、$1,920,197.60 × (1-0.978729) = $40,844.52となります。ご質問にあるように、実際の損失は$84,713.85でした。つまり、「不運」による損失は$84,713.85 - $40,844.52 = $43,869.33となります。
標準偏差でいうと、損失額は$43,869.33 / $9,698 = 4.52です。これ以上の損失が発生する確率は329,101分の1です。
あなたが尋ねたわけではないが、あなたがこれほどまでに落ち込んでいる理由は、すべてが不運なのではなく、部分的にはプレイヤーの戦略ミスによるものではないかと思う。
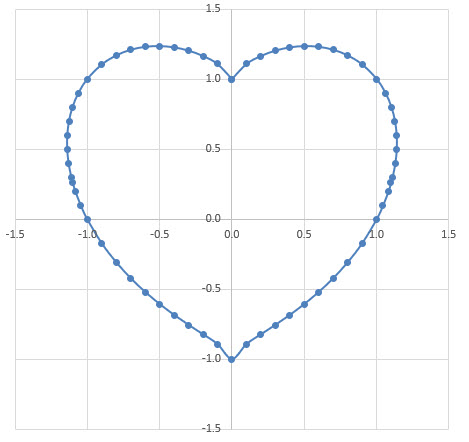
あなたの好きなハートの式は何ですか?
(x 2 + y 2 - 1) 3 = x 2 y 3
ここに私が作成した、この方程式に適合する 63 個のポイントのグラフがあります。