WOO logo

Wizard のオススメ

Wizardに尋ねる #422

議論のために、無限の数のデッキを持つブラックジャックゲームを想定し、無限の再スプリットが許可され、プレイヤーはどのペアでもスプリットするものとします。プレイヤーが最終的にプレイするハンドの数が与えられた場合、その確率はどれくらいでしょうか？

匿名

n回のハンドに再分割する確率は、(combin(2*(n-1),n-1)/n) × (1/13)^(n-1) × (12/13)^n です。最初の項について少し説明が必要だったので、詳しくはカタラン数を調べてください。

以下の表は、1から20までの最終ハンドの確率を示しています。2番目の列は「木」の数で、上記の式ではカタラン数に相当します。

手木々確率
1 1 0.9230769230769
2 1 0.0655439235321
3 2 0.0093080128093
4 5 0.0016523099661
5 14 0.0003285065968
6 42 0.0000699777366
7 132 0.0000156163334
8 429 0.0000036037693
9 1430 0.0000008529631
10 4862 0.0000002059225
11 16796 0.0000000505114
12 58786 0.0000000125531
13 208012 0.0000000031540
14 742900 0.0000000007998
15 2674440 0.0000000002045
16 9694845 0.0000000000526
17 35357670 0.0000000000136
18 129644790 0.0000000000035
19 477638700 0.0000000000009
20 1767263190 0.00000000000002

ピタゴラスの三つ組は無限にあると聞きました。それを求める公式はありますか？

匿名

はい、ピタゴラス数列は無限に存在します！ピタゴラス数列という言葉に馴染みのない方のために説明すると、ピタゴラス数列とは、各辺が整数である直角三角形のことです。最も有名なのは3-4-5です。ピタゴラス数列で、aとbに任意の整数値（a < bで、一方が奇数、もう一方が偶数）を選ぶことで、唯一（つまり約分不可能）な集合が得られます。

  • レッグ1 = b 2 - a 2
  • レグ2 = 2ab
  • 斜辺 = a 2 + b 2

次の表は、すべての辺が 101 以下である、約分できないピタゴラスの三つ組をすべて示しています。

a,b第1レグ第2レグ斜辺
1,2 3 4 5
1,4 8 15 17
1,6 12 35 37
1,8 16 63 65
1,10 20 99 101
2,3 5 12 13
2,5 20 21 29
2,7 28 45 53
2,9 36 77 85
3,4 7 24 25
3,6 27 36 45
3,8 48 55 73
4,5 9 40 41
4,7 33 56 65
4,9 65 72 97
5,6 11 60 61
5,8 39 80 89
6,7 13 84 85

2 つのサイコロを振って、7 が出る前に 7 以外のすべての目が少なくとも 2 回出る確率はどれくらいですか。

Garrison

このような問題のコツは、ロール間の時間が平均 1 の指数分布に従う場合、確率は同じになることです。この場合、次の式で表すことができます。

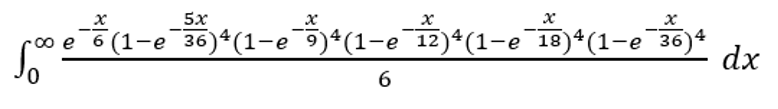
テキスト形式で表すと、exp(-x/6)*(1-exp(-5x/36))^4*(1-exp(-4x/36))^4*(1-exp(-3x/36))^4*(1-exp(-2x/36))^4*(1-exp(-1x/36))^4/6となります。

このような積分を解くには、この積分計算機をお勧めします。

答えは 7864581698887803455719/10946915593544650625105200 =~ 0.0007184290069364848 となります。