クラップス - サイコロと転がし
クラップスのゲームでサイコロを変更して、毎回 7 または 11 が出るようにするにはどうすればいいか知りたいです。助けてください。ありがとうございます。
1 つのサイコロのすべての面に 6 が出て、もう 1 つのサイコロのすべての面に 1 と 5 が出てくるように変更します。
プレイヤー側の「希望的観測」がゲームの結果に影響を与える可能性があると思いますか? 念のため言っておきますが、私は影響の大きさではなく、あなたの哲学的な意見を伺っているだけです。また、クラップスでプレイヤーがサイコロを投げる方法が、結果に(良いか悪いかに関わらず)偏りをもたらす可能性があると思いますか? いつものように、あなたのサイトは素晴らしいです。
親切なお言葉ありがとうございます。いいえ、他の条件が同じであれば、カジノでは希望的観測は役に立たないと思います。
サイコロの影響に関する問題は、激しく議論されているトピックです。個人的には、非常に懐疑的です。2013年にこの回答を見直した今でも、誰かが十分に影響力を発揮して優位に立てるという説得力のある証拠はまだ見当たりません。
サイコロを事前に設定することでクラップスの頻度表を変更することについてあなたの意見を聞きたいです。
私はそれに非常に懐疑的です。このテーマに関するいくつかの実験については、クラップスの付録3で詳しく説明しています。
最近、クラップスのダイスセッティング戦略についていくつか情報を得ました。ダイスを投げる前に特定の方向にセットし、ダイスの回転軸を1つだけに限定することで、特定のダイスセットで7が出る可能性を減らすことができると信じている人がいます。この説は真実なのか、それとも単なる誤解なのかを知りたかったのです。
信じていません。今のところ、私が尊敬する人がこの方法を推奨しているのを見たことがありませんし、効果があるという証拠もありません。可能性を完全に否定するわけではありませんが、非常に懐疑的です。私はネバダ州に住んでいますが、サイコロのセッティングなどに関してはミズーリ州出身です。「見せてくれれば」効果があると。
サイコロは本当に偏りがないのでしょうか? 穴が多く大きな数字の面は、穴が少なく小さな数字の面よりも軽いようです。これは、重い面は裏向きで、大きな数字は表向きで出る可能性が高くなることを示唆しているようです。この原理を利用したクラップスのシステムを想像することはできますが、本当にうまくいくかどうかは疑問です。どう思われますか?
ボードゲームで使われるような普通のサイコロなら、これは当てはまります。しかし、カジノのサイコロには点が埋め込まれています。工場で点のために穴を開け、そこにサイコロ自体と同じ密度の白い点をはめ込みます。つまり、サイコロは実質的に完全な立方体です。たとえボードゲーム用の普通のサイコロを使ったとしても、そのバイアスがハウスエッジを克服するのに十分とは思えません。
カジノ クラップスのテーブルでのサイコロの投げ方は、RNG のように本当にランダムだと思いますか。それとも、サイコロの「仕組み」や単純にずさんな投げ方 (例: ショート スロー) によって、シューターの上手い人と下手な人がいるのでしょうか。現実世界のカジノ クラップスが本当にランダムでないとしたら、これをどう利用すればいいのでしょうか。
生まれつきシューターが下手な人などいないと思います。一部のプロを除けば、サイコロの投げ方は真にランダムと言えるでしょう。クラップスのハウスエッジを歳差運動で克服する方法に関するセミナーもありますが、私はそれらを支持するとも反対するとも言いません。どちらの主張も、十分な証拠をまだ見ていません。
カジノ・プレイヤー誌10月号で、フランク・スコブレット氏がコントロールされたサイコロの投げ方に関する記事を執筆しました。その中で、あなたはスタンフォード・ウォン氏が500回投げて7が74回しか出なかったにもかかわらず、1800ドルを失ったと述べています。なぜそんなに少ないサンプル数(500回)に賭けたのですか?サイコロをコントロールできると主張する人は、少なくとも5万回投げてそのスキルを証明するべきです。500回というサンプル数は、何が起きてもおかしくないほど少ないと考えるのは間違いでしょうか?
1800ドルはスタンフォードではなく、別のギャンブルライターに負けました。もっとたくさんサイコロを振ってほしかったのですが、明らかに時間的な制約がありました。1分間に1回振ると仮定すると、サイコロを5万回振るのに34.7日かかります。500回に決めたのは私ではありませんが、サンプル数と時間のバランスを考えると妥当な妥協点だと思いました。サイコロに影響を与えるかどうかの賛否を論じるには500回では少なすぎるというのはその通りですが、500回振っても全く振らないよりはましです。
ダイスのコントロールに懐疑的なのは承知しています。ダイスのセッティングとコントロールされた射撃を3ヶ月間練習してきました。ランダムに655回投げて、7が78回出る確率はどれくらいでしょうか? 助言ありがとうございます :)
投げる回数が多い場合は、ガウス曲線近似を使用できます。655回投げた場合の7の期待値は、655 × (1/6) = 109.1667です。分散は655 × (1/6) × (5/6) = 90.9722です。標準偏差はsqr(90.9722) = 9.5379です。78個の7は、期待値より109.1667 − 78 = 31.1667少なくなります。これは、(31.1667 - 0.5)/9.5379 = 3.22標準偏差分、期待値より低い値です。期待値より3.22標準偏差以上低い値になる確率は0.000641、つまり1,560分の1です。この数値は、Excel で normsdist(-3.22) という式を使用して取得しました。
これはクラップスにおけるサイコロのコントロールについてです。以前、スタンフォード・ウォンの実験について議論し、「賭けの条件は、精密シューターがサイコロを500回振って7の出目を79.5回未満にできるかどうかでした。ランダムなゲームでの期待値は83.33です。ランダムに500回振って79回以下の7が出る確率は32.66%です。ランダムに500回振って74回以下の7が出る確率は14.41%です。」と述べていました。
この賭けに関して私が疑問に思っているのは、14.41% では依然として「統計的に有意」ではない (つまり p < 0.05) ということです。これは通常、平均値からの標準偏差が 2 より大きい、つまり、一連のどちらかの時点でイベントがランダムに発生する確率が *合計* 5% 未満であることを意味します。
結果が完全にランダムである(つまり、結果が統計的に有意である)可能性が 2.5% 未満であると言えるには、500 回のロールで 7 が何回出なければならないでしょうか。
本当にありがとうございます。ところで、あなたのサイトは、ギャンブルのオッズと確率に関して私が見つけたサイトの中で間違いなく最高のサイトです。これからも頑張ってください。
親切なお言葉をありがとうございます。「ランダムでない結果が出る確率はp」と書くべきではありません。正しくは「ランダムなゲームでそのような結果が出る確率はp」と書くべきです。500回のサイコロ投げで何かを証明したり反証したりするとは誰も思っていませんでした。79.5の7というラインを設定したのも私ではありませんが、統計的に有意になるように設定したとは思えません。むしろ、両者が賭けに同意するポイントだったのではないかと思います。
2.5%の有意水準は、期待値からの標準偏差1.96倍です。これはExcelの式 =normsinv(0.025) で求められます。500回投げた場合の標準偏差は、sqr(500*(1/6)*(5/6)) = 8.333です。つまり、標準偏差1.96倍ということは、期待値より1.96 * 8.333 = 16.333倍低いことになります。500回投げた場合の7の期待値は、500*(1/6) = 83.333です。つまり、標準偏差1.96倍低いということは、83.333 - 16.333 = 67倍です。二項分布を用いて検証すると、7が67個以下になる確率は正確には2.627%です。
3年前のAsk The Wizardコラムで、あなたはこう書いていました。「サイコロに影響を与えるかどうかの賛否を論じるには500回では少なすぎるというのはその通りですが、500回投げた方がゼロよりはましです。」 実験において、サイコロに影響を与えるとされる人物に、多額の賭け金を賭けるのに十分な自信を持つためには何を求めるでしょうか? ブラックジャックのシミュレーションでは、10億ラウンドが「信頼できる」結果の目安となるからです。あなたが考えられる最も効率的な(つまり、最小限の回数で済む)実験設計では、シューターは結果に影響を与えていると確信するために、何回振る必要があるでしょうか? 答えはシューターのスキル次第だとは思いますが、私の言いたいことはお分かりでしょう。最良のシナリオでも100万回も振る必要があるなら、それは無駄な努力になるでしょう。
信頼が得られる明確な基準はありません。それは程度の問題です。まず、何をテストしているのか、そして射手はどのような結果になると予測しているのかを尋ねます。どんなテストでも、2つの誤りが生じる可能性があります。熟練した射手が不運で失敗するか、あるいは偶然射手が幸運で合格するかです。この2つのうち、私は偽陽性を避けたいと考えています。合理的なテストであれば、偽陰性の確率は約5%、偽陽性の確率は約1%に設定できると思います。
例えば、申請者がサイコロを7回振るごとに平均1回7が出ると主張したとします。ランダムシューターは平均して6回に1回7が出ます。試行錯誤の結果、これらの基準の両方を満たすテストは、サイコロを3,600回振り、合格に必要な出目が547回以下、つまり6.58回振るごとに1回7が出るという結果になりました。
7人に1人のシューターは、平均514.3個の7を投げ、標準偏差は21.00です。ガウス近似を用いると、そのような熟練シューターが548個以上の7を投げる確率(偽陰性)は5.7%です。ランダムシューターは平均600個の7を投げ、標準偏差は22.36です。ランダムシューターがテストに合格する確率(偽陽性)は0.94%です。下のグラフは、熟練シューターとランダムシューターの可能性のある結果を示しています。結果が緑の線より左側にある場合、私はそのシューターがテストに合格したと見なし、彼に賭けます。
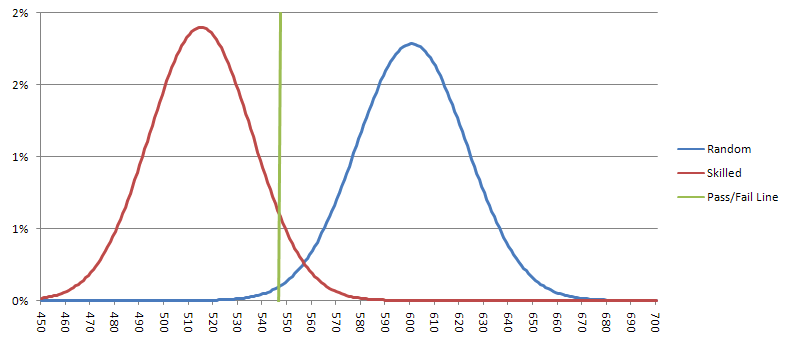
現実的なジレンマは、1分間に2回投げると仮定すると、テストの実施に30時間かかるということです。有意水準をもっと緩く設定して所要時間を短縮することもできるかもしれませんが、結果はそれほど説得力のあるものにはならないでしょう。500ロールのウォン実験よりも大規模なテストを行う時期が来ていると思います。
今日のニュースでは、アトランティックシティの女性がボルガータでサイコロを154回連続で振って7が出たそうです。つまり、彼女は2つのサイコロを154回振って、7が出なかったということです。そこで私は (30/36) 154 を取って、1.5兆分の1以上のオッズを算出しました。メガミリオンズの宝くじに当たる可能性は、サイコロを154回連続で7以外の目が出るマラソンをするよりも約9,000倍も高いのです。これがいかに天文学的な確率の低さか、そしてDNA鑑定の偽造の可能性がわずか数十億分の1しかないことを考えると、あなたはどの程度不正を疑い、この件についてボルガータに相談しようとしますか?私はすでにボルガータに電話して自分の名前を伝え、好きにやってくれと言いました。あなたの考えを聞かせてください。
まず、彼女は合計 154 回サイコロを振り、154 回目は 7 が出ました ( 出典: NJ.com )。しかし、これは最初の 153 回で一度も 7 が出なかったという意味ではありません。カムアウト ロールで何度も 7 が出ていた可能性もあります。2003年 5 月 3 日のコラムで示したように、 154 回目まで投げる確率は 56 億分の 1 です。メガ ミリオンズに当たる確率は、(56,5)*46 = 175,711,536 分の 1 です。つまり、154 回以上投げるのは約 32 倍難しいということです。十分な時間とテーブル (おそらく存在する) があれば、このようなことは遅かれ早かれ起こるはずでした。ですから、私は不正行為を疑うことはありません。このようなことが起こる確率は、どの年でも約 1% だとおおよそ見積もっています。
また、行列で表現された私の解答は、 mathproblems.infoの問題 204 で参照してください。
ラスベガスのカジノの中には、片側に重みのあるサイコロを使っているところがあるようです。証拠として、ストリップ・カジノで集めた244回のサイコロの結果を提出します。公平なサイコロでこれほど偏った結果が出る確率はどれくらいでしょうか?
| ダイステストデータ | |
| サイコロの合計 | 観察 |
| 2 | 6 |
| 3 | 12 |
| 4 | 14 |
| 5 | 18 |
| 6 | 23 |
| 7 | 50 |
| 8 | 36 |
| 9 | 37 |
| 10 | 27 |
| 11 | 14 |
| 12 | 7 |
| 合計 | 244 |
7.7%です。
カイ二乗検定は、このような問題に最適です。この検定を行うには、各カテゴリについて(ae) 2 /e をとります。ここで、a は実際の結果、e は期待される結果です。例えば、244回投げて合計が2になる確率の期待値は、244×(1/36) = 6.777778 です。2が出る確率が1/36である理由がわからない場合は、サイコロの確率の基礎に関する私のページをご覧ください。合計が2になる場合のカイ二乗値は、a=6、e=6.777778 なので、(ae) 2 /e = (6-6.777778) 2 /6.777778 = 0.089253802 となります。
カイ二乗結果
| サイコロの合計 | 観察 | 期待される | カイ二乗 |
| 2 | 6 | 6.777778 | 0.089253 |
| 3 | 12 | 13.555556 | 0.178506 |
| 4 | 14 | 20.333333 | 1.972678 |
| 5 | 18 | 27.111111 | 3.061931 |
| 6 | 23 | 33.888889 | 3.498725 |
| 7 | 50 | 40.666667 | 2.142077 |
| 8 | 36 | 33.888889 | 0.131512 |
| 9 | 37 | 27.111111 | 3.607013 |
| 10 | 27 | 20.333333 | 2.185792 |
| 11 | 14 | 13.555556 | 0.014572 |
| 12 | 7 | 6.777778 | 0.007286 |
| 合計 | 244 | 244 | 16.889344 |
次に、カイ二乗列の合計を求めます。この例では、合計は16.889344です。これはカイ二乗統計量と呼ばれます。「自由度」の数は、データのカテゴリ数より1少ない数で、この場合は11-1=10です。最後に、統計表でカイ二乗統計量10.52と自由度10を調べるか、Excelで=chidist(16.889344,10)という数式を使用します。どちらの場合も、結果は7.7%です。つまり、公平なサイコロでこれほど歪んだ結果が出る確率は7.7%です。つまり、これらの結果は予想よりも歪んでいますが、それほど問題視するほど歪んではいません。このテストを続ける場合は、合計ではなく、各サイコロの個々の結果を収集することをお勧めします。また、あるカテゴリーの結果の期待値が低い場合、カイ二乗検定は適切ではないことにも留意すべきです。最小期待値5というのは、よく言われる数値です。
クラップスで2つのサイコロが重なって出たらどうなるでしょうか?有効なロールと言えるでしょうか?もしそうなら、ディーラーは下のサイコロの目が何だったかをどのように伝えるのでしょうか?
有効なロールとみなされるかどうかは、場所によって異なります。ニュージャージー州の賭博規則19:47-1.9(a)には次のように規定されています。
サイコロのどちらか一方または両方がテーブルから外れた場合、または一方のサイコロがもう一方のサイコロの上に止まった場合、サイコロの振りは無効となります。 -- NJ 19:47-1.9(a)
ペンシルベニア州にも全く同じ規制、 第537.9条(a)があります。
サイコロのどちらか一方または両方がテーブルから外れた場合、または一方のサイコロがもう一方のサイコロの上に止まった場合は、サイコロのロールは無効となります。 -- PA 537.9(a)
ラスベガスのサイコロディーラーに尋ねたところ、ここでは有効なロールとみなされるのは、そうでなければ有効な投げ方だと教えてくれました。ディーラー自身も実際にそのような場面を見たことはないそうですが、もし実際にそのような場面があったとしても、ディーラーは上のサイコロを動かして下のサイコロの目を確認するだけだと言っていました。しかし、上のサイコロに触れたり、透かしたりしなくても、下のサイコロの出目を知ることは可能です。その方法をご紹介します。まず、4つの面を見ることで、上のサイコロの可能性を2つに絞り込むことができます。3つの可能性に基づいて、どのように判断するかをご説明します。
- 1 または 6:3 を探します。一番上の点が 5 に接している場合は、1 が上です。そうでない場合、2 に接している場合は、6 が上です。
- 2または5:3を探します。一番上の点が6に接している場合は、2が上です。そうでない場合、1に接している場合は、5が上です。
- 3 または 4:2 を探します。一番上の点が 6 に接している場合は、3 が上です。そうでない場合、一番上の点が 1 に接している場合は、4 が上です。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
2 個のサイコロを振って、出た目の合計が 2 から 12 までの各値に少なくとも 1 回発生すると予想される回数はいくつですか。
この質問はTwoPlusTwo.comで出題され、 BruceZ氏によって正解されました。以下の解答はBruceZ氏と同じ方法で、BruceZ氏には敬意を表すべきでしょう。難しい解答ですので、ご注意ください。
まず、合計2が出るまでの期待される回数を考えてみましょう。2が出る確率は1/36なので、最初の2が出るまで平均36回振る必要があります。
次に、2と3の両方が出るのに必要なサイコロの期待回数を考えてみましょう。2が出るまでには平均36回振る必要があることは既に分かっています。2が出るのを待っている間に3が出れば、3が出るまで追加でサイコロを振る必要はありません。しかし、そうでない場合は、3が出るまでにさらにサイコロを振る必要があります。
3が出る確率は1/18なので、2が先に出た場合、3が出るまで平均18回追加でサイコロを振る必要があります。2が出る可能性は1通り、3が出る可能性は2通りあるので、2が先に出る確率は1/(1+2) = 1/3です。
つまり、3が出るのに18回追加で振る必要がある確率は1/3です。したがって、2と3の両方が出るのに必要な期待値は36+(1/3)×18 = 42となります。
次に、4が出るまであと何回サイコロを振る必要があるかを考えてみましょう。2と3を振った時点でまだ4が出ていない場合、4が出るまでには平均してあと12回サイコロを振る必要があります。これは、4が出る確率が1/12だからです。
2と3を達成する前に4を達成する確率はどれくらいでしょうか?まず、AとBが互いに排他的でない場合の一般的な確率の法則を確認しましょう。
pr(A または B) = pr(A) + pr(B) - pr(A および B)
pr(A and B) を減算するのは、その偶然性が pr(A) + pr(B) に二重にカウントされているからです。つまり、
pr(4 が 2 または 3 の前) = pr(4 が 2 の前) + pr(4 が 3 の前) - pr(4 が 2 と 3 の前) = (3/4)+(3/5)-(3/6) = 0.85。
2と3が出るまでの過程で4が出ない確率は1.0 - 0.85 = 0.15です。つまり、12回追加で振る必要がある確率は15%です。したがって、2、3、4が出るまでの期待値は42 + 0.15 * 12 = 43.8となります。
次に、5が出るまであと何回サイコロを振る必要があるかを考えてみましょう。2~4を振った時点でまだ5が出ていない場合、5が出る確率は4/36 = 1/9なので、平均してあと9回サイコロを振る必要があります。
2、3、4を達成する前に5を獲得する確率はどれくらいでしょうか?一般的なルールは次のとおりです。
pr (A または B または C) = pr(A) + pr(B) + pr(C) - pr(A および B) - pr(A および C) - pr(B および C) + pr(A および B および C)
つまり、pr(5が2または3または4より前) = pr(5が2より前)+pr(5が3より前)+pr(5が4より前)-pr(5が2と3より前)-pr(5が2と4より前)-pr(5が3と4より前)+pr(5が2、3、4より前) = (4/5)+(4/6)+(4/7)-(4/7)-(4/8)-(4/9)+(4/10) = 83/90 です。2から4までの過程で4が出ない確率は、1 - 83/90 = 7/90 です。つまり、7.2回追加で振る必要がある確率は7.78%です。したがって、2、3、4、5が出るのに必要なロール回数の期待値は、43.8 + (7/90)*9 = 44.5となります。
同じ論理を、合計6から12まで繰り返します。最後の数字が毎回ほぼ倍増するため、次の数字が出る確率を求めるために必要な計算回数は、12に達するまでに1,023回になります。
pr(A or B or C or ... or Z)の一般的なルールは次のとおりです。
pr(A または B または C または ... または Z) =
pr(A) + pr(B) + ... + pr(Z)
- pr (AとB) - pr(AとC) - ... - pr(YとZ) 2つのイベントのすべての組み合わせの確率を引きます
+ pr (AとBとC) + pr(AとBとD) + ... + pr(XとYとZ) 3つのイベントのすべての組み合わせの確率を加算します
- pr (AとBとCとD) - pr(AとBとCとE) - ... - pr(WとXとYとZ) 4つのイベントのすべての組み合わせの確率を引きますこれを繰り返しながら、奇数事象には確率を加算し、偶数事象には確率を減算することを忘れないようにしてください。起こり得る事象の数が多い場合は、当然ながらこの作業は面倒になり、スプレッドシートやコンピュータプログラムが実質的に必要になります。
以下の表は、各ステップにおける期待値を示しています。例えば、2が出る場合は36、2と3が出る場合は42です。右下のセルには、11個の合計目をすべて出すために必要なロールの期待値が61.217385であることを示しています。
期待されるロール回数の問題
| 必要な最大数 | 確率 | 必要に応じて予想されるロール | 確率は必要ない | 必要な確率 | 予想総ロール数 |
|---|---|---|---|---|---|
| 2 | 0.027778 | 36.0 | 0.000000 | 1.000000 | 36.000000 |
| 3 | 0.055556 | 18.0 | 0.666667 | 0.333333 | 42.000000 |
| 4 | 0.083333 | 12.0 | 0.850000 | 0.150000 | 43.800000 |
| 5 | 0.111111 | 9.0 | 0.922222 | 0.077778 | 44.500000 |
| 6 | 0.138889 | 7.2 | 0.956044 | 0.043956 | 44.816484 |
| 7 | 0.166667 | 6.0 | 0.973646 | 0.026354 | 44.974607 |
| 8 | 0.138889 | 7.2 | 0.962994 | 0.037006 | 45.241049 |
| 9 | 0.111111 | 9.0 | 0.944827 | 0.055173 | 45.737607 |
| 10 | 0.083333 | 12.0 | 0.911570 | 0.088430 | 46.798765 |
| 11 | 0.055556 | 18.0 | 0.843824 | 0.156176 | 49.609939 |
| 12 | 0.027778 | 36.0 | 0.677571 | 0.322429 | 61.217385 |
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
ウィザードによると、あのウェブサイトは、非難を正当化する確かな証拠が全くないまま、わめき散らかしているだけだそうだ。もし証拠があれば、偏ったサイコロを使っているカジノがあれば喜んで告発するよ。
偏りのあるサイコロの正当な証拠をお持ちの方がいらっしゃいましたら、喜んで調査し、結論を発表させていただきます。私が見たい証拠は、サイコロを振ったログファイル、あるいは、偏りがあるとされる実際のサイコロです。
さらに、カジノが本当に予想よりも多くの 7 が出るサイコロを使用していたとしたら、なぜこれらの刑事たちは、パスしないことに賭けてオッズを設定した陰謀に気づかないのでしょうか。
スロットマシンのホットロールボーナスラウンドでは、2つのサイコロの合計に応じて、以下の枚数のコインがプレイヤーに付与されます。プレイヤーは7が出るまでコインを集め続け、7が出るとボーナスは終了します。最初のサイコロで7が出た場合は、70枚のコインが付与されます。7以外の合計が出た場合の賞金は以下の通りです。
- 2または12:1,000
- 3または11:600
- 4または10:400
- 5または9:300
- 6または8:200
私の質問は、平均ボーナス賞金はいくらですか?
答えは次のボタンをクリックしてください。
解決策については次のボタンをクリックしてください。
[ネタバレ] 答えをxとします。プレイヤーが7を出さない限り、過去のすべての勝利に加えて、将来の勝利もxになると常に期待できます。言い換えれば、サイコロを振るという行為には記憶を持たない性質があり、これまで何回振ったとしても、最初の7に近づくことはありません。サイコロの確率の基本については詳しく説明しません。それぞれの合計の確率は次のようになります。
- 2: 1/36
- 3: 2/36
- 4: 3/36
- 5: 4/36
- 6: 5/36
- 7: 6/36
- 8: 5/36
- 9: 4/36
- 10: 3/36
- 11: 2/36
- 12: 1/36
慰めの賞品を考慮する前に、x の値は次のように表すことができます。
x = (1/36)*(1000 + x) + (2/36)*(600 + x) + (3/36)*(400 + x) + (4/36)*(300 + x) + (5/36)*(200 + x) + (5/36)*(200 + x) + (4/36)*(300 + x) + (3/36)*(400 + x) + (2/36)*(600 + x) + (1/36)*(1000 + x)次に、両辺を 36 倍します。
36x = (1000 + x) + 2*(600 + x) + 3*(400 + x) + 4*(300 + x) + 5*(200 + x) + 5*(200 + x) + 4*(300 + x) + 3*(400 + x) + 2*(600 + x) + (1000 + x)36倍 = 11,200 + 30倍
6倍 = 11,200
x = 11,200/6 = 1866.67。
次に、慰安賞の価値は 700*(6/36) = 116.67 です。
したがって、ボーナスの平均勝利額は 1866.67 + 116.67 = 1983.33 となります。
[/spoiler]


