ノンカジノゲーム - よくある質問
ドル札でライアーズポーカーをするのが好きです。1枚の紙幣に同じ数字が1、2、3、4、または5つ出る確率はどれくらいですか?ありがとうございます。3人でプレイする場合、数字が1つ出る確率はどれくらいですか?
まず、特定の数字がランダムな紙幣にn回出現する確率について、まだ聞かれていない質問に答えましょう。紙幣には8桁の数字が印刷されているので、特定の数字がn回出現する確率は、combin(8,n)*0.1 n *0.9 8-n /10 8となります。0から8までの特定の数字の出現確率を示す表を以下に示します。
特定の数字のオッズライアーズポーカー
| 番号 | 確率 |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| 合計 | 1.00000000 |
次の表は、あらゆる種類の紙幣の確率を、それぞれのn枚の紙幣の枚数ごとに分類したものです。例えば、シリアル番号66847680には、3枚揃いの紙幣が1枚、ペアが1枚、シングルトンが3枚含まれており、確率は0.1693440です。
ライアーズポーカーにおける一般的な確率
| 8オーク | 7オーク | 6オーク | 5オーク | 4オーク | 3オーク | 2オーク | オーク1本 | 確率 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| 合計 | 1.0000000 | |||||||
オーク = 「一種の」
詳細については、私のLiars Pokerのページを参照してください。
バンク・オブ・アメリカは、ATMで行った選択された1日分の入金を3倍にするキャンペーンを提供しています。このキャンペーンは約2ヶ月間続きます。300ドルを入金する場合、100ドルを3回入金するのと、300ドルを1回入金するのとでは、どちらの方が当選確率が高いのでしょうか?それとも、全体的な当選確率が非常に低いため、その差に労力をかける価値はないのでしょうか?
預想される勝利は、総預金を何回分割しても同じです。良い戦略は、できるだけ多くの回数で同じ金額を預け入れと引き出しを繰り返すことでしょう。ただし、オッズが非常に悪い場合は、その手間をかける価値がないかもしれません。
東洋のサイコロゲームについて質問です。プレイヤーはサイコロのどの面が出るかを推測します。まず、ルーレットのように1、2、3、4、5、6に賭け、次にディーラーが3つのサイコロを同時に振ります。配当は、選んだ数字が3つのサイコロのいずれかに1回出れば1:1、2回出れば2:1、3つのサイコロすべてに出れば3:1です。プレイヤーはボードに何度でも賭けることができますが、最適な賭け回数はいくつでしょうか?(賭け金がすべて同じ額だと仮定した場合)
3つ揃う確率は1/216です。2つ揃う確率は3*5/216です。1つ揃う確率は25*5/216です。0つ揃う確率は5*5*5/216です。したがって、期待リターンは3*(1/216)+2*(15/216)+1*(75/216)-1*(125/216)=-17/216=-7.87%となります。最適なベット回数というものはなく、どのような賭け方をしても、期待される総資金の7.87%を失うことになります。
これらの賭けはシックボーとチャック・ア・ラックの両方で行うことができます。
Windows 版のような標準的なクロンダイク ソリティア ゲームで勝つ確率はどれくらいですか?
これはおそらく私が最もよく受ける質問ですが、答えが分かりません。徹底的なクロンダイクソリティアは未だかつて存在していません。コンピューターの速度が100万倍になったら、いつか誰かがクリアするかもしれません。しかし、少なくとも1950年代にはラスベガスのカジノでこのゲームが提供されていたという噂があります。何人かのラスベガスのベテランに確認してもらいましたが、今のところ誰も確認できていません。
最近バックギャモンをしていて、ダブル6が4回連続で出ました。また同じことが起こる確率はどれくらいでしょうか?
新しいロールごとに、次の 4 回のロールがすべて 6 のダブル 6 になる確率は (1/36) 4 = 1679616 分の 1 です。
こんにちは。www.transience.com.au/ pearl.html に「Pearls for Swine」というゲームがあります。真珠は3列(5+4+3)にまとめられており、自分の番になると、1列から好きなだけ真珠を取り除けます。ゲームの目的は、最後の真珠を相手に取らせることです。プレイヤー(私)が常に先攻で、そして常に負けます。なぜ私は勝てないのでしょうか?相手は常に勝つための巧妙なシステムを持っているのですが、その秘密を教えていただけますか?
まず、3つの真珠がある列から真珠を2つ取り除き、1+4+5とします。次のターンで相手が何をしても、1+1+1、1+2+3、または4+4のいずれかを残します。いずれの場合も、相手は2つ以上の真珠が2つ、または1つの真珠が奇数個ある状況に追い込まれます。
モノポリーで一番良いセットは何ですか?
オレンジセットが一番好きです。投資収益率が最も高いです。例えば、オレンジセットのホテルは500ドルで、平均賃料は966.67ドル、賃料対経費率は1.93です。これより高い比率を持つのはライトブルーセットだけで、2.27です。しかし、ライトブルーの最大賃料はわずか600ドルです。オレンジセットに3軒の家を建てた場合の賃料は、ライトブルーのホテルと同じですが、20%安く、さらに建てる余地があります。また、オレンジセットは刑務所から出てきたばかりなので、着地するのに最適です。ですから、私のアドバイスに従って、取引をする際はオレンジセットを選ぶようにしてください。
じゃんけんをするときのアドバイスは何ですか?
このサイトにある最高のアドバイスは、次の通りです。最初のラウンドでは、必ず「紙」を選びましょう。アマチュア プレイヤーは最初は石を選ぶ傾向があるためです。各ポジションで 1 つずつ手を差し出せば、石が最も快適で自然な選択であることがわかります。繰り返しラウンドをプレイする場合は、最後のラウンドで相手に勝つ確率が 3 分の 1 未満になるものを選ぶ必要があります。アマチュアが繰り返す確率は 3 分の 1 未満だと考えているからです。頭に入り込みそうなプロとプレイする場合は、時計の秒針を見てランダムに秒数を 3 で割って余りを取り、その余りを 0=石、1=チョキ、2=紙 (または事前に決めておけば他のマッピングでも可) のようにマッピングします。そのため、次にオランダ風のレストランに行くときは、チェックのために 1 ラウンドプレイしてから紙を選ぶことをお勧めします。後で感謝してくれるでしょう。
リスクで攻撃側がサイコロを 3 個振り、防御側がサイコロを 2 個振った場合、どちらが有利でしょうか?
このゲームを知らない人のために説明すると、リスクは史上最高のボードゲームです。プレイしたことがない人は、まだ人生を謳歌していないと言えるでしょう。よくある3対2の対戦では、以下のような結果が考えられます。
- 守備側が両方負ける: 37.17%
- それぞれ1つずつ失う: 33.58%
- 攻撃側は両方を失う: 29.26%
Yahtzee ゲームで、カードに Yahtzee だけが残っている場合、それが完成する確率はどれくらいですか?
次の表は、Yahtzee を作成するために必要な追加のサイコロの数に応じて、最後のロールでの成功確率を示しています。
ヤッツィーの最終ロールの確率
| 必要 | 確率 成功の |
| 0 | 1 |
| 1 | 0.166667 |
| 2 | 0.027778 |
| 3 | 0.00463 |
| 4 | 0.000772 |
次の表は、改善の確率を示しています。左の列は、特定のサイコロを振る前に必要なサイコロの数を示し、上の列は、特定のサイコロを振った後に必要なサイコロの数を示しています。表の中央には、与えられた改善度の確率が示されています。
改善の可能性
| ロール前に必要なもの | 0 | 1 | 2 | 3 | 4 | 合計 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.833333 | 0 | 0 | 0 | 1 |
| 2 | 0.027778 | 0.277778 | 0.694444 | 0 | 0 | 1 |
| 3 | 0.00463 | 0.069444 | 0.37037 | 0.555556 | 0 | 1 |
| 4 | 0.000772 | 0.01929 | 0.192901 | 0.694444 | 0.092593 | 1 |
次の表は、最初のロールで Yahtzee を作成するために 0 ~ 4 個の追加のサイコロが必要になる確率を示しています。
ヤッツィーの初ロールの確率
| 必要 | 確率 |
| 0 | 0.000772 |
| 1 | 0.019290 |
| 2 | 0.192901 |
| 3 | 0.694444 |
| 4 | 0.092593 |
次の表は、1回目のロール後に必要なサイコロの数に応じて、改善の確率と最終的な成功率を示しています。例えば、プレイヤーがヤッツィーを出すのにあと3個のサイコロが必要な場合、2回目のロール後にあと2個必要になり、3回目のロールでヤッツィーを出す確率は0.010288066です。
2回目のロールの前後に必要な数に応じた、1回目のロール後のヤッツィーの確率
| ロール前に必要なもの | 0 | 1 | 2 | 3 | 4 | 合計 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.166667 | 0.138889 | 0 | 0 | 0 | 0.305556 |
| 2 | 0.027778 | 0.046296 | 0.01929 | 0 | 0 | 0.093364 |
| 3 | 0.00463 | 0.011574 | 0.010288 | 0.002572 | 0 | 0.029064 |
| 4 | 0.000772 | 0.003215 | 0.005358 | 0.003215 | 0.000071 | 0.012631 |
最終的な答えを得るには、2つ上の表で最初のロールを終えた後に必要な数字と、1つ上の表の最終列で最終的に成功する確率の内積を取ります。これは0.092593*0.012631 + 0.694444*0.029064 + 0.192901*0.093364 + 0.019290*0.305556 + 0.000772*1 = 4.6028643%です。これを確認するために、1億回のゲームシミュレーションを実行したところ、シミュレーションの確率は4.60562%でした。
じゃんけんのゲームにダイナマイトが選択肢として導入され、ダイナマイトはじゃんけんに勝ち、じゃんけんはダイナマイトに勝つ場合、完璧な論理学者 2 人がプレイする場合の最適な戦略は何でしょうか。
まず、紙で遊ぶことはあり得ません。相手が何を投げたとしても、ダイナマイトを紙の上に投げれば、同等かそれ以上の勝率が得られます。紙がなくなると、ダイナマイトは事実上、新しい紙となり、石に勝ち、ハサミに負けます。つまり、完璧な戦略は、石、ハサミ、ダイナマイトの中からランダムに、そして等確率で選ぶことです。
限られた時間内にできるだけ多くのお金を集めなければならないブースで、お金が飛び交う状況での最善の戦略は何でしょうか?
ギャンブルゲームがあるとします。公平なコインを繰り返し投げます。1回投げるごとに1ルピーを支払う必要があります。結果はHかTの2通りです。表と裏の差が3になった場合、ギャンブラーから8ルピーを受け取ります。このゲームに参加すべきでしょうか?また、その理由は何でしょうか?勝つ確率はどれくらいでしょうか?7ルピーや9ルピーを受け取る場合、勝つ確率にどのような影響があるでしょうか?
開始点からの予想されるフリップ回数を x とします。
片側が多数派で 1 回投げた場合の残りの予想投げ回数を y とします。
片側が多数派で 2 回投げた場合の残りの予想回数を z とします。
E(x) = 1 + E(y)
E(y) = 1 + 0.5*E(x) + 0.5*E(z)
E(z) = 1 + 0.5*E(y)
すると、E(x) = 9、E(y) = 8、E(z) = 5 であることが簡単に分かります。つまり、表裏の差が3になるには平均9回投げる必要があります。つまり、8ルピーの場合、1回につき1ルピーを受け取る人にとっては良い賭けです。なぜなら、平均9ルピーを受け取りますが、支払うのは8ルピーだけだからです。ギャンブラーのハウスエッジは11.11%です。9ルピーなら妥当な賭けですが、7ルピーならハウスエッジは22.22%です。
2002年11月28日のコラムで、残り3列になった時の遊び方を説明しました。4列になった時の戦略は以下の通りです。自分の番になったら、左の列の配置を確認し、右の列の配置に従ってプレイしてください。例えば、開始位置の3456は最後に記載されており、5列の真珠から4個取り除いて1346にする必要があります。左の列に「負け」と表示されている場合、相手が最適な戦略を採用した場合、勝つ方法はありません。Transcienceのゲームでは常に最適な戦略が採用されているようです。
この表のパターンは、相手を、最小の列と最大の列にある真珠の合計が中央の2つの列の合計と等しくなるように追い込むというものです。これには、真珠の数が最も少ない列に0を残すことも含まれます。
豚に真珠II戦略
| あなたが持っている | 離れる |
| 1111 | 111 |
| 1112 | 111 |
| 1113 | 111 |
| 1114 | 111 |
| 1115 | 111 |
| 1116 | 111 |
| 1122 | 失う |
| 1123 | 1122 |
| 1124 | 1122 |
| 1125 | 1122 |
| 1126 | 1122 |
| 1133 | 失う |
| 1134 | 1133 |
| 1135 | 1133 |
| 1136 | 1133 |
| 1144 | 失う |
| 1145 | 1144 |
| 1146 | 1144 |
| 1155 | 失う |
| 1156 | 1155 |
| 1222 | 1122 |
| 1223 | 1122 |
| 1224 | 1122 |
| 1225 | 1122 |
| 1226 | 1122 |
| 1233 | 123 |
| 1234 | 123 |
| 1235 | 123 |
| 1236 | 123 |
| 1244 | 1144 |
| 1245 | 145 |
| 1246 | 246 |
| 1255 | 1155 |
| 1256 | 失う |
| 1333 | 1133 |
| 1334 | 1133 |
| 1335 | 1133 |
| 1336 | 1133 |
| 1344 | 1144 |
| 1345 | 145 |
| 1346 | 失う |
| 1355 | 1155 |
| 1356 | 1256 |
| 1444 | 1144 |
| 1445 | 1144 |
| 1446 | 1144 |
| 1455 | 1155 |
| 1456 | 1346 |
| 2222 | 失う |
| 2223 | 2222 |
| 2224 | 2222 |
| 2225 | 2222 |
| 2226 | 2222 |
| 2233 | 失う |
| 2234 | 2233 |
| 2235 | 2233 |
| 2236 | 2233 |
| 2244 | 失う |
| 2245 | 2244 |
| 2246 | 2244 |
| 2255 | 失う |
| 2256 | 2255 |
| 2333 | 2233 |
| 2334 | 2233 |
| 2335 | 2233 |
| 2336 | 2233 |
| 2344 | 2244 |
| 2345 | 失う |
| 2346 | 1346 |
| 2355 | 2255 |
| 2356 | 2345 |
| 2444 | 2244 |
| 2445 | 2244 |
| 2446 | 2244 |
| 2455 | 2255 |
| 2456 | 2345 |
| 3333 | 失う |
| 3334 | 3333 |
| 3335 | 3333 |
| 3335 | 3333 |
| 3336 | 3333 |
| 3344 | 失う |
| 3345 | 3344 |
| 3346 | 3344 |
| 3355 | 失う |
| 3356 | 3355 |
| 3444 | 3344 |
| 3445 | 3344 |
| 3446 | 3344 |
| 3455 | 3355 |
| 3456 | 1346 |
Brad S. さんから、真珠の数や列の数に関係なく、一般的な戦略を追加するというご意見をいただきました。まず、各列を2つの要素に分解します。例えば、トランサイエンスゲームの開始位置は次のようになります。
- 3 = 2 + 1
- 4 = 4
- 5 = 4+1
- 6 = 4 + 2
次に、2の累乗をそれぞれ偶数個残すように努めます。例えば、上の例では1が2個、2が2個、4が3個あります。つまり、4が1個余ります。次に、4の項がある行から4を1つ取り除きます。これを繰り返し、相手の1の数が2、2、または奇数になるまで続けます。
この戦略をパール3で試せば、必ず勝てます。私が10ゲーム目(4+7+8+11)でやったように、負けそうな状況から始める場合は、「GO」をクリックして相手に先攻を取らせましょう。
2進数に関しては正しい戦略ですが、必ずしも勝利の戦略とは言えません。まず、相手に1の行を奇数個残せるならそうしましょう。そうでない場合は、各行を2進数の要素に分解します。例えば、99は64+32+2+1です。次に、すべての行の各要素の数を合計します。そして、すべての行で相手にすべての2進数の要素が偶数個残るようなプレイを探します。
例を見てみましょう。次のようなシナリオであなたの番が来たとします。
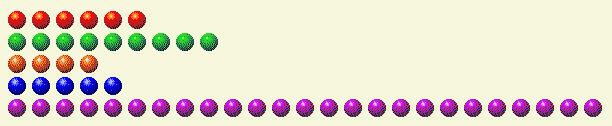
次の表は、各行をバイナリ コンポーネントに分解します。
プレイヤーのターン1
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 25 | 1 | 0 | 0 | 1 | 1 |
| 合計 | 3 | 1 | 3 | 2 | 1 |
1、2、4、16が奇数であることがわかります。16を消すには、25の列を16より小さくする必要があります。2進数の要素の合計を偶数にするには、1を消し、2を足し、4を足し、8を残し、16を消す必要があります。つまり、最善のプレイは最後の列で2+4+8=14となることです。一番下の列に14を残すと、次のようになります。
コンピュータのターン1
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 合計 | 2 | 2 | 4 | 2 | 0 |
コンピューターが順番に処理して、これを私たちに残します。
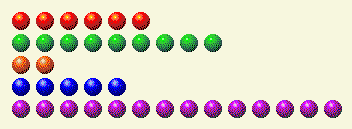
そのバイナリ内訳は次のとおりです。
プレイヤーのターン2
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| 合計 | 2 | 3 | 3 | 2 | 0 |
ここで2と4を1つずつ取り除いて合計を均等にする必要があります。両方の要素を含む行は14だけです。そこから6を引いて8にします。
コンピュータのターン2
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 合計 | 2 | 2 | 2 | 2 | 0 |
コンピューターが順番に処理して、これを私たちに残します。
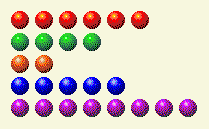
ここで、1、4、8 列を変更する必要があります。
プレイヤーのターン3
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| 合計 | 1 | 2 | 3 | 1 | 0 |
それは、次のように 8 行目を 5 行目に変更することで実行できます。
コンピュータのターン3
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 合計 | 2 | 2 | 4 | 0 | 0 |
コンピューターが順番に処理して、これを私たちに残します。
ここで、合計 2 と 4 を変更する必要があります。
プレイヤーのターン4
| 行 | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 合計 | 2 | 3 | 3 | 0 | 0 |
これは 6 を 0 に変更することで実行できます。
コンピュータのターン4
| 行 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 合計 | 2 | 2 | 2 | 0 | 0 |
コンピューターが順番に処理して、これを私たちに残します。
ここで 2 と 4 を変更する必要があります。
プレイヤーのターン5
| 行 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 合計 | 2 | 3 | 1 | 0 | 0 |
これは、5 列を 3 列に変更することで実現できます。相手を x、x、y、y の状況に追い込むことができれば、最後まで同じ状況を維持できれば、必ず勝つことができます。
コンピュータのターン5
| 行 | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 合計 | 2 | 4 | 0 | 0 | 0 |
次の数手は、コンピューターをx,x,y,yのパターンに誘導します。ここでコンピューターは2,2,3,2のパターンを残したので、私も2,2,2,2のパターンに誘導します。

するとコンピューターは2、2、1、2と答えます。私は2、2、1、1のままにしておきます。
するとコンピューターは2、2、1を残します。私は2、2を残します。もし相手が2列を同じ数にできれば、必ず勝ちます。列を同じ数に保っていれば大丈夫です。

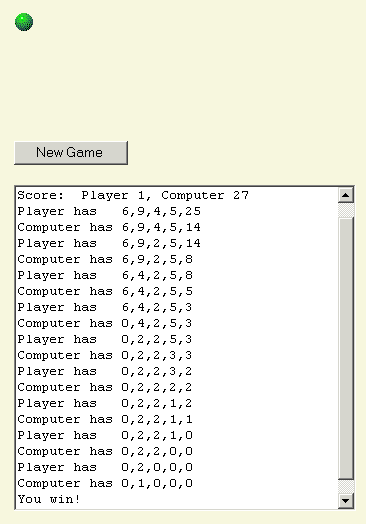
すると、コンピューターは 2 枚のカード 1 組を残し、私は 1 枚を取り除きます。

ここでゲームは終わりです。
最近、大叔父が使っていたカーニバルホイールを手に入れました。100年ほど前のもので、それを使ってゲームを作ろうとしています。1から60までの番号がランダムに振られていて、15目ごとに黒と赤が交互に表示され、緑の星が出てきます。1回転あたりの配当はいくらにすべきか、教えていただけますか?
つまり、黒が30個、赤が30個、緑が4個あるとします。黒の確率は30/64、赤が30/64、緑が4/64となります。ある事象の確率がpの場合、公平なオッズは(1-p)/p対1です。つまり、赤のオッズは(34/64)/(30/64) = 34対30 = 17対15となります。黒も同様です。緑のオッズは(60/64)/(4/64) = 60対4 = 15対1です。特定の数字の場合、公平なオッズは(63/64)/(1/64)対63対1となります。
赤と黒に1対1、緑に14対1、そして個々の数字に60対1の配当を推奨します。ハウスエッジの計算式の一つは(ta)/(t+1)です。ここで、tは真のオッズ、aは実際のオッズです。この場合、赤または黒に賭けた場合のハウスエッジは(63-60)/(63+1) = 3/64 = 4.69%です。緑に賭けた場合のハウスエッジは(15-14)/(15+1) = 1/16 = 6.25%です。個々の数字に賭けた場合のハウスエッジは(63-60)/(63+1) = 3/64 = 4.69%です。
ニューヨーク州では、場外馬券売り場にビデオ宝くじ端末(VLT)が設置されています。VP機が「熱くなり」、次々と勝ち役を出すようになると、その機械は「設定点」に近づいていると表現されます。同じ機械が、ある日は配当を出し、別の日は出金しないのは、このためだと考えられます。また、これらの機械のほとんどは、勝ち役を失うことはありません。もしその役を捨てれば、同等かそれ以上の役が返ってくるはずです。この件について、あなたはどうお考えですか?
VLTは、いわばプルタブゲームを改良したものです。結果のプールはあらかじめ決められています。プレイすると、ゲームはプールからランダムに結果を選び、スロットマシンやビデオポーカーの形でプレイヤーに勝利結果を表示します。結果はあらかじめ決まっているため、スキル要素は架空のものです。例えば、ロイヤルフラッシュが配られてそれを捨てたとしても、ドローでもう一度ロイヤルフラッシュが手に入ります。普段はギャンブルでは過去は関係ないと言いますが、この場合は除去効果があります。一度プレイして負けると、残りのゲーム結果の確率はわずかに上がります。仮想プルタブがなくなり、仮想ドラムが補充されるまでは、おそらくそうでしょう。あなたの運の良し悪しは単なる運であり、運命づけられたものはすべて想像上のものだと私は信じています。
その後、ある読者がこのトピックに次のように付け加えました。
2月14日号の「魔法使いに聞く」(第183回)についてコメントがあります。ご回答いただいた質問とは全く関係ありませんが、もし興味を持っていただけたら幸いです。
クラス3ゲーミングの完全導入を認めた提案1Aが可決される以前、私たちは数年間、VLTスタイルの小規模なシステムを導入していました。SDG(現在はBally傘下)が運営していた当時のシステムでは、賞金プールは当初400万回分でした。プールが縮小され200万回分が残った時点で、次の400万回分が追加され、合計600万回分になりました。プールが再び200万回分に縮小されると、このプロセスが繰り返されました。
ヤッツィーを獲得するために必要な予想ロール回数はどれくらいですか?
プレイヤーが常に最も多く出現する数字を持っていると仮定すると、平均は11.09になります。以下は、8260万回のランダムシミュレーションにおけるロール回数の分布を示す表です。
ヤッツィー実験
| ロール | 発生事例 | 確率 |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0.0333975 |
| 4 | 4504806 | 0.0545376 |
| 5 | 5776444 | 0.0699327 |
| 6 | 6491538 | 0.0785901 |
| 7 | 6727992 | 0.0814527 |
| 8 | 6601612 | 0.0799227 |
| 9 | 6246388 | 0.0756221 |
| 10 | 5741778 | 0.0695131 |
| 11 | 5174553 | 0.0626459 |
| 12 | 4591986 | 0.0555931 |
| 13 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0.042285 |
| 15 | 3008766 | 0.0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0.0265529 |
| 18 | 1864107 | 0.0225679 |
| 19 | 1575763 | 0.019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0.0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 25 | 554937 | 0.00671837 |
| 26 | 463901 | 0.00561624 |
| 27 | 387339 | 0.00468933 |
| 28 | 324079 | 0.00392347 |
| 29 | 271321 | 0.00328476 |
| 30 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 32 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 34 | 109592 | 0.00132678 |
| 35 | 91327 | 0.00110565 |
| 36 | 76216 | 0.00092271 |
| 37 | 63433 | 0.00076795 |
| 38 | 52786 | 0.00063906 |
| 39 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 42 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 44 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 47 | 10299 | 0.00012469 |
| 48 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0。00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 38 | 0.00000046 |
| 78 | 42 | 0.00000051 |
| 79 | 27 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| 合計 | 82600000 | 1 |
バックギャモンのオッズ/統計/確率について優れた分析を行っているウェブサイトをご存じですか? また、ゲームのあらゆる側面についてお勧めできる本はありますか?
バックギャモンは私のお気に入りのギャンブルゲームの一つです。対人戦は分析が非常に難しいため、このゲームについて書くことはありません。また、このゲームで新しい発見も見つけられていません。ですから、アドバイスは他の人に任せたいと思います。以下に、私がお勧めするリソースをご紹介します。
ポール・マグリエル著『バックギャモン』 :もしバックギャモンのバイブルがあるとしたら、まさにこれでしょう。私は古いハードカバー版を所有しており、誇りをもっています。この本はバックギャモン入門に最適です。1976年に書かれた本ですが、そこに書かれているアドバイスは今でも通用します。
ビル・ロバーティー著『 501 Essential Backgammon Problems』 :この本を何年も読み通そうと努力していますが、まだ半分しか進んでいません。問題の半分を間違えてしまうのは、ゴルフと同じくらいバックギャモンが下手なんじゃないかと思うほどで、本当にがっかりです。しかし、間違えた問題一つ一つから、貴重な教訓が得られます。中級者から上級者にとって、この本は価値ある、そして謙虚になれる学習ツールです。
Snowie バックギャモンソフトウェア:このソフトで年間約1000回プレイしています。Snowie はほぼ完璧なプレイをするだけでなく、ミスをするとその損失額を正確に教えてくれます。他にも私がまだ試していない機能がたくさんあります。Snowie から学んだことが一つあるとすれば、私のゲームの最大の問題は、時に完全に明白なプレイを見落としてしまう愚かなミスだということです。チェスと同じように、たった一つの悪い手が100の良い手を打ち消すこともあるのです。
Motifウェブサイト:Snowieを購入する前、Motifと数え切れないほど対戦しました。Motifの戦略は非常に堅実だと思います。自分のゲームを向上させるには、より強い相手と対戦することほど良いものはありません。
以下の表は、各プレイヤーの勝利確率を、最初のプレイヤーの最初のスピンに基づいて示しています。プレイヤー1が最初にスピンし、次にプレイヤー2、最後にプレイヤー3がスピンします。一番下の行は、最初のスピン前の全体的な勝利確率を示しています。
プライス・イズ・ライト・ショーケース対決における確率
| スピン1 | 戦略 | プレイヤー1 | プレイヤー2 | プレイヤー3 |
| 0.05 | スピン | 20.59% | 37.55% | 41.85% |
| 0.10 | スピン | 20.59% | 37.55% | 41.86% |
| 0.15 | スピン | 20.57% | 37.55% | 41.87% |
| 0.20 | スピン | 20.55% | 37.55% | 41.9% |
| 0.25 | スピン | 20.5% | 37.56% | 41.94% |
| 0.30 | スピン | 20.43% | 37.56% | 42.01% |
| 0.35 | スピン | 20.33% | 37.58% | 42.10% |
| 0.40 | スピン | 20.18% | 37.60% | 42.22% |
| 0.45 | スピン | 19.97% | 37.64% | 42.39% |
| 0.50 | スピン | 19.68% | 37.71% | 42.61% |
| 0.55 | スピン | 19.26% | 37.81% | 42.93% |
| 0.60 | スピン | 18.67% | 37.96% | 43.36% |
| 0.65 | スピン | 17.86% | 38.21% | 43.93% |
| 0.70 | 滞在する | 21.56% | 38.28% | 40.16% |
| 0.75 | 滞在する | 28.42% | 35.21% | 36.38% |
| 0.80 | 滞在する | 36.82% | 31.26% | 31.92% |
| 0.85 | 滞在する | 46.99% | 26.35% | 26.66% |
| 0.90 | 滞在する | 59.17% | 20.36% | 20.47% |
| 0.95 | 滞在する | 73.61% | 13.19% | 13.21% |
| 1.00 | 滞在する | 90.57% | 4.72% | 4.72% |
| 平均 | 30.82% | 32.96% | 36.22% |
6×20 6の組み合わせのうち、当選する数字は次のとおりです。
プレイヤー1: 118,331,250プレイヤー2: 126,566,457
プレイヤー3: 139,102,293
自宅でポーカーをプレイする際の「エーシー・デューシー」の正しい戦略は何ですか? 3枚目のカードが最初の2枚のうちの1枚と一致した場合、ベットはプッシュになります。
3枚目のカードが揃うとプッシュになるというあなたのプレイスタイルでは、最初の2枚のカードの間に6つ以上のランクがある場合(6枚のスプレッド)、オッズが有利になります。私がオレンジカウンティでプレイした方法では、3枚目のカードが揃うとダブル負けになりました。このルールでは、8枚のスプレッドでオッズは均衡します。3枚目のカードが揃うと1倍の負けになる場合は、オッズが有利になるためには7枚のスプレッドが必要です。
ワンカードポーカーは、エース、デュース、スリーの3枚のカードデッキを使用します。エースが最も低く、スリーが最も高くなります。2人のプレイヤーはそれぞれ1ドルをポットに賭けます。その後、各プレイヤーは1枚のカードを受け取ります。ベットの順番は事前に決められており、プレイヤー1が最初に行動します。プレイヤー1は1ドルをベットするかチェックするかを選択できます。プレイヤー1がベットした場合、プレイヤー2はコールまたはフォールドを選択できます。プレイヤー1がチェックした場合、プレイヤー2は1ドルをベットするかチェックするかを選択できます。プレイヤー1がチェックし、プレイヤー2がベットした場合、プレイヤー1はコールまたはフォールドを選択できます。両方のプレイヤーがチェックするか、両方がベットした場合、より高いカードを持つプレイヤーがポットを獲得します。両方のプレイヤーが完璧な論理的思考力を持っていると仮定した場合、各プレイヤーにとって最適な戦略は何でしょうか?
一日中この作業に取り組んだので、ご満足いただけたでしょうか。解答と解説は、私の別のサイトmathproblems.info の問題203、またはJason Swanson著の学術論文「ゲーム理論とポーカー」に掲載されています。
住宅ローンを検討しています。ある会社は30年固定金利で5.75%プラス1ポイントの金利を提示しています。別の会社は5.875%プラス1ポイントの金利を提示しています。どちらの会社がより良いのでしょうか?
他の読者のために、ポイントとはローンに対して課される手数料のことです。例えば、25万ドルのローンの場合、1ポイントは2,500ドルになります。借り手はポイントを元本残高に加算し、元本を早期に返済することは決してないと仮定します。
以下の表は、1 ポイントの利率と期間に応じて、ポイントなしの等価利率を示します。
ポイントなしの同等金利
| 1ポイントの金利 | 10年 | 15年 | 20年 | 30年 | 40年 |
| 4.00% | 4.212% | 4.147% | 4.115% | 4.083% | 4.067% |
| 4.25% | 4.463% | 4.398% | 4.366% | 4.334% | 4.318% |
| 4.50% | 4.714% | 4.649% | 4.617% | 4.585% | 4.570% |
| 4.75% | 4.965% | 4.900% | 4.868% | 4.836% | 4.821% |
| 5.00% | 5.216% | 5.151% | 5.119% | 5.088% | 5.073% |
| 5.25% | 5.467% | 5.402% | 5.370% | 5.339% | 5.324% |
| 5.50% | 5.718% | 5.654% | 5.621% | 5.590% | 5.576% |
| 5.75% | 5.969% | 5.905% | 5.873% | 5.842% | 5.827% |
| 6.00% | 6.220% | 6.156% | 6.124% | 6.093% | 6.079% |
| 6.25% | 6.471% | 6.407% | 6.375% | 6.344% | 6.330% |
| 6.50% | 6.723% | 6.658% | 6.626% | 6.596% | 6.582% |
| 6.75% | 6.974% | 6.909% | 6.878% | 6.847% | 6.834% |
| 7.00% | 7.225% | 7.160% | 7.129% | 7.099% | 7.085% |
| 7.25% | 7.476% | 7.412% | 7.380% | 7.350% | 7.337% |
| 7.50% | 7.727% | 7.663% | 7.631% | 7.602% | 7.589% |
| 7.75% | 7.978% | 7.914% | 7.883% | 7.853% | 7.841% |
| 8.00% | 8.229% | 8.165% | 8.134% | 8.105% | 8.093% |
| 8.25% | 8.480% | 8.416% | 8.385% | 8.357% | 8.344% |
| 8.50% | 8.731% | 8.668% | 8.637% | 8.608% | 8.596% |
| 8.75% | 8.982% | 8.919% | 8.888% | 8.860% | 8.848% |
| 9.00% | 9.233% | 9.170% | 9.140% | 9.112% | 9.100% |
| 9.25% | 9.485% | 9.421% | 9.391% | 9.363% | 9.352% |
| 9.50% | 9.736% | 9.673% | 9.642% | 9.615% | 9.604% |
| 9.75% | 9.987% | 9.924% | 9.894% | 9.867% | 9.856% |
| 10.00% | 10.238% | 10.175% | 10.145% | 10.119% | 10.108% |
これは、1ポイント付与後の5.75%の金利は、ポイント付与なしの5.842%と同等であることを示しています。つまり、ポイントが元本残高に加算されると仮定すると、どちらの場合も支払額は同じになります。別のご提案では、ポイント付与なしの5.875%が提示されており、これは5.842%よりも高いため、ポイント付与後の5.75%をお選びください。
PS i をどうやって解いたのか気になる方のために、Excel のrate 関数を使用しました。
息子が2週間で2回ホールインワンを達成しました。確率はどれくらいでしょうか?息子のハンディキャップは1です。1ホール目は151ヤード、2ホール目は137ヤードで、それぞれ異なるコースで達成しました。
グレゴリー・ベア著『人生:オッズ(そして改善する方法)』によれば、PGAツアーのパー3ホールでホールインワンを達成する確率は2491分の1です。これらの距離はパー3の範囲に当てはまると思います。
ハンディキャップ1は非常に良いので、PGAツアー選手と比べてそれほど優遇するつもりはありません。例えば、あなたの息子さんのパー3ホール1ホールあたりの確率が3,000分の1だとしましょう。一般的なゴルフコースにはパー3ホールが4つほどあります。息子さんが毎日プレーするとしましょう。そうすると、週に28ホールのパー3ホールをプレーすることになります。ちょうど2回ホールインワンを達成する確率は、(28,2)×(1/3000) 2 ×(2999/3000) 26 = 24,017分の1になります。
最近、7,033個の賞品がある抽選に参加しました。当選確率は13分の1だそうです。5枚購入しました。当選確率は実際どれくらいでしょうか?また、高額賞品が40個あるのですが、高額賞品が当たる確率はどれくらいでしょうか?
話を簡単にするために、チケットを多く買えば買うほど、自分自身と競争することになるため、1枚あたりの価値が下がるという事実は無視しましょう。とはいえ、5枚のチケット全てが外れてしまう確率は(12/13) 5 = 67.02%です。つまり、少なくとも1つの賞品が当たる確率は32.98%です。購入前のチケットは合計7033×13=91,429枚あります。そのうち91,429-40=91,389枚は高額賞品ではありません。5枚のチケットで高額賞品が1つも当たらない確率は(91,389/91429) 5 = 99.78%です。つまり、少なくとも1つの高額賞品が当たる確率は0.22%、つまり458分の1です。
ハートのゲームでは、各プレイヤーに13枚のカードが配られます。13枚のうち最も多くのカードを持つスーツは「ロングスーツ」と呼ばれ、4枚から13枚のカードで構成されます。それぞれの合計の確率はどれくらいでしょうか?
ハートのロングスーツの確率
| カード | 組み合わせ | 確率 |
| 4 | 222766089260 | 0.35080524800183 |
| 5 | 281562853572 | 0.44339660045899 |
| 6 | 105080049360 | 0.16547685914958 |
| 7 | 22394644272 | 0.03526640326564 |
| 8 | 2963997036 | 0.00466761219692 |
| 9 | 235237860 | 0.00037044541245 |
| 10 | 10455016 | 0.00001646424055 |
| 11 | 231192 | 0.00000036407412 |
| 12 | 2028 | 0.00000000319363 |
| 13 | 4 | 0.00000000000630 |
| 合計 | 635013559600 | 1 |
72の法則とは、年間収益率を72で割ることで、資金が2倍になるまでの年数を算出するというものです。例えば、年間10%の利回りの投資の場合、価値が2倍になるまでに72÷10=7.2年かかります。ここで少し突飛な疑問なのですが、なぜ72年なのでしょうか?
まず、「72の法則」は、お金を2倍にするために必要な期間の概算であり、正確な答えではありません。以下の表は、様々な年利における「72の法則」の値と正確な年数を示しています。
72の法則 — お金を2倍にする年数
| 金利 | 72の法則 | ちょうど | 違い |
|---|---|---|---|
| 0.01 | 72.00 | 69.66 | 2.34 |
| 0.02 | 36.00 | 35.00 | 1.00 |
| 0.03 | 24.00 | 23.45 | 0.55 |
| 0.04 | 18時 | 17.67 | 0.33 |
| 0.05 | 14.40 | 14.21 | 0.19 |
| 0.06 | 12時 | 11.90 | 0.10 |
| 0.07 | 10.29 | 10.24 | 0.04 |
| 0.08 | 9.00 | 9.01 | -0.01 |
| 0.09 | 8.00 | 8.04 | -0.04 |
| 0.10 | 7.20 | 7.27 | -0.07 |
| 0.11 | 6.55 | 6.64 | -0.10 |
| 0.12 | 6.00 | 6.12 | -0.12 |
| 0.13 | 5.54 | 5.67 | -0.13 |
| 0.14 | 5.14 | 5.29 | -0.15 |
| 0.15 | 4.80 | 4.96 | -0.16 |
| 0.16 | 4.50 | 4.67 | -0.17 |
| 0.17 | 4.24 | 4.41 | -0.18 |
| 0.18 | 4.00 | 4.19 | -0.19 |
| 0.19 | 3.79 | 3.98 | -0.20 |
| 0.20 | 3.60 | 3.80 | -0.20 |
なぜ72なのでしょうか?ぴったり72である必要はありません。これは、投資で実際に見られる金利に見合うだけの数字です。7.8469%の金利とほぼ正確に一致します。πやeのように、72という数字に特別な意味はありません。なぜどんな数字でも使えるのでしょうか?金利をiとすると、投資額を2倍にするのにかかる年数(y)を求めましょう。
2 = (1+i) y
ln(2) = ln(1+i) y
ln(2)= y×ln(1+i)
y = ln(2)/ln(1+i)
これは私の最高の答えではないかもしれませんが、次のロジックに従ってみてください: y=ln(x) とします。
dy/dx=1/x です。
x の値が 1 に近い場合、1/x =~ x となります。
したがって、x の値が 1 に近い場合、dy/dx は ~ 1 になります。
したがって、x の値が 1 に近い場合、ln(x) の傾きは 1 に近くなります。
したがって、x の値が 0 に近い場合、ln(1+x) の傾きは 1 に近くなります。
「72 の法則」とは、.72/i =~ .6931/ln(1+i) であることを意味します。
i の値が 0 に近い場合、i と ln(1+i) は類似していることが分かりました。
したがって、iの値が0に近い場合、1/iと1/ln(1+i)は類似します。
69.31の代わりに72を使用すると、iの値が約8%の場合のiとln(1+i)の差が調整されます。
少しでも意味が伝われば幸いです。私の微積分はちょっと錆び付いていて、これを自分で説明するのに何時間もかかりました。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
最近のストリートフェアで、数字が書かれたマスと浅いカップ、そしてボールが入ったカップが置かれたゲームがありました。足し算をするゲームです。ゲームの名前は聞かずに、インターネットで1時間ほど検索してみましたが、何も見つかりませんでした。オッズとか、少なくとも名前だけでも何か情報をお持ちではないかと思いました。
そのゲームは業界ではラズルダズルと呼ばれています。子供の頃、南カリフォルニアで見たのを覚えています。去年はメキシコのサンフェリペでも見かけました。たいていはフットボールの試合に見せかけるように加工されています。このゲームは、カーニバルゲーム詐欺の中でも最悪だと思います。ニューヨーク州は、こんなゲームを許可しているなんて恥じ入るべきです。調べてみたところ、ルールは場所によって違いますが、詐欺の本質はどれも同じです。
これはクラップスのフィールドベットと同じ錯覚に基づいています。フィールドベットを知らない読者のために説明すると、2つのサイコロを振って出た目の合計が2、3、4、9、10、11、または12であれば勝ちとなります。外れとなる数字は5、6、7、8です。勝った場合は配当は均等ですが、2が出た場合は2倍、12が出た場合は3倍となります(ただし、ケチなハラーズカジノでは12のみ2倍となります)。数学が苦手なギャンブラーは、7つの合計が勝ち、4つの合計が負けなので、これは良い賭けだと誤解するかもしれません。オッズがハウスに有利なのは、外れとなる数字が出る可能性が最も高いからです。
以下は、1978 年 11 月の The American Statistician 誌に掲載された Donald A. Berry と Ronald R. Regal による記事「Probabilities of Winning a Certain Carnival Game」から抜粋した、Razzle Dazzle の具体的なルールです。
- このゲームの目的は、サッカー場を100ヤード進むことです。100ヤード進むと、プレイヤーには素敵な賞品が贈られます。
- プレイヤーはプレイごとに 1 ドルなどの指定された料金を支払い始めます。
- プレイヤーは11×13のマス目に8個のビー玉を落とします。それぞれのビー玉は143個の穴のいずれかに落ちます。
- 各ホールには 1 から 6 までのポイントがあります。次の表は、各ポイント数の頻度を示しています。
ラズルダズルポイントの分配
ポイント 番号
機内で確率 1 11 0.076923 2 19 0.132867 3 39 0.272727 4 44 0.307692 5 19 0.132867 6 11 0.076923 合計 143 1.000000 - 合計ポイントが加算されます。カーニバルのスタッフは、ポイントの合計を換算表で調べ、選手が何ヤード進んだかを確認します。換算表は以下の通りです。
Razzle Dazzle変換チャート
ポイント ヤード
獲得8 100 9 100 10 50 11 30 12 50 13 50 14 20 15 15 16 10 17 5 18歳から38歳 0 39 5 40 5 41 15 42 20 43 50 44 50 45 30 46 50 47 100 48 100 - プレーヤーが合計 29 を出した場合、それ以降のすべてのロールの料金は 2 倍になり、プレーヤーがフットボール フィールドの反対側の端に到達した場合に、追加の賞品が 1 つ与えられます。
ビー玉1個あたりの平均点は3.52、標準偏差は1.31です。3点と4点の確率が最も高いことに注目してください。これにより標準偏差が低くなり、多くのビー玉の合計が期待値に近くなります。ちなみに、サイコロ1個を振った場合の標準偏差は1.71です。
次に、ヤード換算表に勝ち合計が20、負け合計が21あることに注目してください。カーニバルゲームでギャンブルをするような愚か者は、自分が勝ち進む確率を20/41、つまり48.8%と誤って判断するかもしれません。カーニバルの主催者が、これが勝ち進む確率だと嘘をついたとしても驚きません。しかし、フィールドベットと同様に、最も可能性の高い結果では何も勝ちません。
次の表は、1ターンあたりの得点数、獲得ヤード数、期待獲得ヤード数の確率を示しています。右下のセルは、1ターンあたりの平均獲得ヤード数が0.0196であることを示しています。
1ターンあたりの期待獲得ヤード
| ポイント | 確率 | ヤード 獲得 | 期待される ヤード 獲得 |
| 8 | 0.00000000005 | 100 | 0.00000000464 |
| 9 | 0.00000000176 | 100 | 0.00000017647 |
| 10 | 0.00000002586 | 50 | 0.00000129285 |
| 11 | 0.00000022643 | 30 | 0.00000679305 |
| 12 | 0.00000143397 | 50 | 0.00007169849 |
| 13 | 0.00000713000 | 50 | 0.00035650022 |
| 14 | 0.00002926510 | 20 | 0.00058530196 |
| 15 | 0.00010234709 | 15 | 0.00153520642 |
| 16 | 0.00031168305 | 10 | 0.00311683054 |
| 17 | 0.00083981462 | 5 | 0.00419907311 |
| 18 | 0.00202563214 | 0 | 0.00000000000 |
| 19 | 0.00441368617 | 0 | 0.00000000000 |
| 20 | 0.00874847408 | 0 | 0.00000000000 |
| 21 | 0.01586193216 | 0 | 0.00000000000 |
| 22 | 0.02642117465 | 0 | 0.00000000000 |
| 23 | 0.04056887936 | 0 | 0.00000000000 |
| 24 | 0.05757346716 | 0 | 0.00000000000 |
| 25 | 0.07566411880 | 0 | 0.00000000000 |
| 26 | 0.09221675088 | 0 | 0.00000000000 |
| 27 | 0.10431970222 | 0 | 0.00000000000 |
| 28 | 0.10958441738 | 0 | 0.00000000000 |
| 29 | 0.10689316272 | 0 | 0.00000000000 |
| 30 | 0.09677806051 | 0 | 0.00000000000 |
| 31 | 0.08125426057 | 0 | 0.00000000000 |
| 32 | 0.06317871335 | 0 | 0.00000000000 |
| 33 | 0.04540984887 | 0 | 0.00000000000 |
| 34 | 0.03009743061 | 0 | 0.00000000000 |
| 35 | 0.01833921711 | 0 | 0.00000000000 |
| 36 | 0.01023355162 | 0 | 0.00000000000 |
| 37 | 0.00520465303 | 0 | 0.00000000000 |
| 38 | 0.00239815734 | 0 | 0.00000000000 |
| 39 | 0.00099365741 | 5 | 0.00496828705 |
| 40 | 0.00036673565 | 5 | 0.00183367827 |
| 41 | 0.00011909673 | 15 | 0.00178645089 |
| 42 | 0.00003349036 | 20 | 0.00066980729 |
| 43 | 0.00000797528 | 50 | 0.00039876403 |
| 44 | 0.00000155945 | 50 | 0.00007797235 |
| 45 | 0.00000023832 | 30 | 0.00000714969 |
| 46 | 0.00000002632 | 50 | 0.00000131607 |
| 47 | 0.00000000176 | 100 | 0.00000017647 |
| 48 | 0。00000000005 | 100 | 0.00000000464 |
| 合計 | 1.00000000000 | 0 | 0.01961648451 |
以下は、1,750 万のゲームのランダム シミュレーションの結果です。
Razzle Dazzleシミュレーション結果
| 質問 | 答え |
| ターンごとの前進確率 | 0.0028 |
| 1ターンあたりの期待獲得ヤード | 0.0196 |
| 昇格ごとの予想獲得ヤード | 6.9698 |
| ゲームあたりの予想ターン数 | 5238.7950 |
| 1試合あたりの平均ダブルス数 | 559.9874 |
| ゲームあたりの平均賞金 | 560.9874 |
ゲームごとの平均賭け金総額を表示したかったのですが、私のコンピュータはそれほど大きな数値を処理できません。平均的なゲームでは、プレイヤーは1ゲームあたり平均5,239ターンで560回賭け金を倍増していました。シミュレーションでは、あるゲームでプレイヤーは1,800回賭け金を倍増していました。平均560回の倍増でも、開始賭け金を1ドルと仮定すると、1回の賭け金は3.77 × 10 168ドルになります。これは、既知の宇宙に存在する原子の数よりも桁違いに大きい値です(出典)。
355プレイに1回しか進めないなら、どんなにナイーブなプレイヤーでも長くはプレイできないでしょう。カーニーは最初はプレイヤーに有利になるようにズルをします。フリーロールを仕掛けたり、ポイントの集計で嘘をついて勝利点を出してプレイヤーの自信を高めようとします。私はこのゲームをプレイしたことはありませんが、プレイヤーがレッドゾーン(タッチダウンから20ヤード以内)に近づくと、カーニーはフェアプレーを始めるだろうと想像しています。プレイヤーはなぜ突然何も進まなくなったのかと不思議に思うかもしれませんが、既にお金を投資し、ゴールラインにも非常に近いため、せっかく支払ったヤード数を放棄して立ち去ることには躊躇するでしょう。
リンク
- Razzle Dazzle 、本『On the Midway』からの抜粋。
- Razzle Dazzle Carny ボードゲーム アーケード詐欺。
- あるカーニバルゲームに勝つ確率(ドナルド・A・ベリー、ロナルド・R・リーガル著)
最近のカーニバルで、三目並べ風のゲームがありました。1回1ポンドで、底に9つのポケットがある大きな木箱に向かって、ものすごく弾むボールを3つ投げます。すべてのボールがそれぞれ異なるマスに落ちると仮定した場合、勝つ確率はどれくらいでしょうか?
2人が勝つ方法は8通りあります。3つの行、3つの列、そして2つの対角線です。9つのマス目から3つのマス目を選ぶ組み合わせは(9,3)=84通りあります。したがって、勝つ確率は8/84 = 9.52%です。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
モノポリーをプレイするときのアドバイスは何ですか?
これが私のウィザードのモノポリーの基本戦略です。
- すべて買いましょう。上級プレイヤーは、独占に役立たず、他のプレイヤーを妨害せず、交渉材料としての価値も低い物件については例外を認める場合があります。資金が不足している場合は、公共料金の支払いを拒否されることもあります。
- できる限り上手にトレードしましょう。ここがスキルの出番です。できるだけ良いセットとトレードしましょう。一般的には、オレンジ、黄色、水色、紺色、薄紫、赤、緑、濃紫の順です。状況によって順位は変わります。資金が少ないゲームでは、水色のように開発コストが安いセットを優先しましょう。資金が多いゲームでは、黄色や濃青のように、より多くの資金を投入できる可能性のあるセットを狙いましょう。
- 自然に、あるいはトレードで、資産が一つ増えたら、すぐに資産を増やしましょう。それぞれの土地でできるだけ早く3軒建てるようにしましょう。3軒を超えると、1軒あたりの限界収益率は下がります。残りの物件のほとんどを抵当に入れ、手持ちの現金を使いましょう。ちょっとした出費のために、少しの自己資金を残しておきましょう。お金を使わないのは、戦場で弾丸を使わない兵士のようなものです。
- くだらないハウスルールには反対しましょう。特に「フリーパーキング」のマネーポット(あれは我慢できない!)は大嫌いです。対戦相手よりも実力があるなら、ゲームのランダム性を最小限に抑えたいはずです。
猿がルービックキューブで遊んでいた場合、どの時点でも解けたパターンになる確率はどれくらいでしょうか?
立方体の中心6面は固定されています。面を回転させることでできるのは、角と辺の配置を変えることだけです。立方体を分解すると、各ピースの向きに関係なく、8つの角の配置は8!=40,320通りになります。同様に、12の辺の配置は12!=479,001,600通りになります。
各コーナーの向きは3通りあり、合計で3 8 =6,561通りあります。同様に、各エッジピースの向きは2通りあり、合計で2 12 =4,096通りあります。
つまり、立方体を分解し、辺と角のグループを並べ替えると、8! × 12! × 3 8 × 2 12 = 519,024,039,293,878,000,000通りの順列が考えられます。ただし、これらの順列の全ては、開始位置から面を回転させることによって得られるわけではありません。
まず、一つの角だけを回転させ、他の部分はそのままにしておくことは不可能です。どんな回転の組み合わせでも、そのような結果を得ることはできません。基本的に、すべての動作には必ず反応が伴います。一つの角を回転させると、他のピースが何らかの形で乱れてしまいます。同様に、一つの端のピースだけを回転させることも不可能です。これらの理由から、順列の数は3 × 2 = 6で割る必要があります。
第二に、キューブの残りの部分を乱さずに 2 つのエッジ ピースを交換することは不可能です。これが、この答えを説明するのが最も難しい部分です。ルービック キューブでできることは、一度に 1 つの面を回転させることだけです。1 回の動作で 4 つのエッジ ピースと 4 つのコーナー ピースが回転し、合計 8 つのピースが移動します。回転のシーケンスは、8 で割り切れるピースの移動回数で表すことができます。一連の動作の結果、2 つの動作が互いに打ち消し合うことがよくあります。ただし、どのような回転のシーケンスでも、移動するピースの数は常に偶数になります。2 つのエッジ ピースを交換することは 1 回の動作、つまり奇数であり、偶数のセットの合計では実現できません。数学者はこれをパリティ問題と呼びます。したがって、他のピースを乱さずに 2 つのエッジ ピースを交換することはできないため、さらに 2 で割る必要があります。
つまり、ルービックキューブの順列は3 × 2 × 2 = 12通りあります。ルービックキューブを分解してランダムに組み立て直した場合、解ける確率は1/12です。つまり、ルービックキューブの順列の総数は8! × 12! × 3 12 × 2 12 / 12 = 43,252,003,274,489,900,000通りです。もし、地球上の人口とほぼ同じ70億匹の猿がルービックキューブをランダムに、1秒間に1回転の速度で遊んでいたとすると、キューブは平均して196年に1回、解けた位置を通過します。
リンク
ハートをプレイしていて、10枚のカードが配られました。その確率はどれくらいですか?
ハーツのルールを知らない方のために説明すると、まず4人のプレイヤーにそれぞれ13枚のカードが配られます。ハートのマークはゲームにおいて重要な意味を持つため、何枚配られるかが重要です。以下の表は、0~13枚のハートが配られる確率を示しています。
13枚のカードのうちハートが0~13枚になる確率
| ハート | 組み合わせ | 確率 | 逆 |
|---|---|---|---|
| 13 | 1 | 0.0000000000016 | 635,013,559,600.0分の1 |
| 12 | 507 | 0.0000000007984 | 1,252,492,228.0分の1 |
| 11 | 57,798 | 0.0000000910185 | 10,986,773.9分の1 |
| 10 | 2,613,754 | 0.0000041160601 | 242,950.8分の1 |
| 9 | 58,809,465 | 0.0000926113531 | 10,797.8分の1 |
| 8 | 7億4099万9259 | 0.0011669030492 | 857.0分の1 |
| 7 | 5,598,661,068 | 0.0088166008164 | 113.4分の1 |
| 6 | 26,393,687,892 | 0.0415639752774 | 24.1分の1 |
| 5 | 79,181,063,676 | 0.1246919258321 | 8.0分の1 |
| 4 | 151,519,319,380 | 0.2386080062219 | 4.2分の1 |
| 3 | 181,823,183,256 | 0.2863296074662 | 3.5分の1 |
| 2 | 130,732,371,432 | 0.2058733541286 | 4.9分の1 |
| 1 | 50,840,366,668 | 0.0800618599389 | 12.5分の1 |
| 0 | 8,122,425,444 | 0.0127909480376 | 78.2分の1 |
| 合計 | 635,013,559,600 | 1.0000000000000 |
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
プレイヤーのデスクでチケットを印刷し、それをドラムに入れるという、電子チケットではなく、通常のドラムに入った通常のチケットを使用するカジノのプロモーションでは、ドラムに入れる前にチケットを曲げたり、折り目をつけたりしていますか? 折り目がついたチケットの方が当選確率が高いと思いますか?
皆さんが幸せでありますように。この質問に答えるために、オフィス・デポで大きなチケットのロールを買いました。そのうち500枚を紙袋に入れ、半分は90度くらいの角度で半分に折り、もう半分は広げておきました。そして、6人のボランティアにそれぞれ40~60枚ずつ、順番を入れ替えながら引いてもらい、結果を記録しました。結果は以下の通りです。
抽選チケット実験
| 主題 | 折り畳まれた | 展開 | 合計 |
|---|---|---|---|
| 1 | 25 | 25 | 50 |
| 2 | 38 | 22 | 60 |
| 3 | 25 | 15 | 40 |
| 4 | 34 | 16 | 50 |
| 5 | 27 | 23 | 50 |
| 6 | 26 | 24 | 50 |
| 合計 | 175 | 125 | 300 |
つまり、抽選されたチケットの 58.3% が折り返されたことになります。
フォールドが影響しないと仮定した場合、これらの結果は期待値から標準偏差2.89倍離れることになります。フォールドがオッズに影響を与えないと仮定した場合、この枚数、あるいはそれ以上のフォールドされたチケットが当たる確率は0.19%、つまり514分の1です。
さらに付け加えると、急いでチケットを引いた被験者は、折り紙付きのチケットを引く可能性がはるかに高かった。一方、時間をかけて慎重に引いた被験者は、その確率はほぼ50/50であった。
だから、私の結論は、間違いなく折りたたむことです。
この質問についての議論については、 Wizard of Vegasの私のフォーラムをご覧ください。