確率 - カード
私はオンラインでバカラをプレイしていて、75ハンドのうちバンカーが52、プレイヤーが23を獲得しました。差は29ですがその確率はどのくらいですか?
まずはあなたが同点を数えていないと仮定します。言い換えれば、75ベットが解決されたことを意味します。引き分けなしで75手になる可能性は非常に低いでしょう。解決された75ベットのうち、バンカーが勝つと予想される数は38.00913745です。標準偏差は75の積の平方根、バンカーが勝つ確率、およびプレイヤーが勝つ確率です。同点がなかった場合、バンカーが勝つ確率は0.506788499であり、プレイヤーが勝つ確率は0.493211501です。したがって、標準偏差は4.329727904になります。次に、二項分布の半点補正を行って 標準正規分布表 でZ統計を検索する必要があります(この手順は読者に任されています)。最終的な答えとしては、バンカーが52勝以上を獲得する確率は.0009であるということです。あなたの質問はまた.0004の確率を持つバンカーが23回以下(また29回以上の差)勝つ可能性を考慮に入れると29以上の差の確率は最終的に.0013で769分の1になります。
褒めていただきありがとうございます。5倍ほど違っています。ディーラーの手札では順序が関係するためです。ディーラーの最初のカードは表向きで配られるからです。正しい組み合わせの計算式は、combin(52,5)*47*combin(46,4) = 19,933,230,517,200となります。
5 カード ドロー ポーカーで 3 枚のカードを引いてペアになり、フルハウスになる確率はどれくらいですか?
この状況でフルハウスを作るには2つの方法があります。(1) スリーカードを引く、(2) ペアともう1枚のペアを引く。ここではシングルトンを3枚捨てると仮定します。
まず、(1) の組み合わせの数を計算してみましょう。3段で3スーツしか残っていない場合(シングルトンを3つ捨てたことを思い出してください)、9段で4スーツしか残っていない場合、組み合わせの数は3*combin(3,3)+9*combin(4,3) = 3*1 + 9*4 = 39となります。
次に、(2)の組み合わせの数を計算してみましょう。既存のペアに加えるスーツは2つ残っています。残り3枚のカードで3列からペアを作る方法はcombin (3,2)通り、残り4枚のカードで3列からペアを作る方法はcombin(4,2)通りです。したがって、(2)の組み合わせの総数は2*(3*combin(3,2)+9*combin(4,2)) = 2*(3*3 + 9*6) = 126通りです。フルハウスを作る方法は、(1)と(2)の合計、つまり39+126=165通りです。2回目のドローで3枚のカードを並べる方法はcombin(47,3)=16,215通りあります。フルハウスが出る確率は、フルハウスが出る方法の数を合計の組み合わせ数で割った値で、165/16,215 = 0.0101758、つまり約 98 分の 1 となります。
combin() 関数の詳細については、ポーカーの確率に関するセクションを参照してください。
友人と週に一度ポーカーを始めました(ファイブカード・ドロー、スタッド、セブンカード・スタッド)。テーブルには7人のプレイヤーがいます。52枚のデッキからカードが配られるため、プレイヤーの数が多いことで手札の確率が大幅に低下するように思えます。適切な方向に導いてくれる数学的な公式はありますか?
いいえ、特定の手札が配られる確率は、テーブルにいる他のプレイヤーの数に関係なく同じです。見えないカードは見えないカードであり、他のプレイヤーが持っているかデッキに残っているかは関係ありません。
最近、信じられない話を聞きました。友人が自宅でポーカーをしていた時、友人と二人ともカードを一枚も引かずに、同じ手でナチュラル・ストレート・フラッシュを出したそうです!(5枚のカードを引く時)これはとても信じられない話です。あなたのサイトで計算したところ、ストレート・フラッシュが1枚出る確率は約65,000対1だそうですが、ゲームに6人のプレイヤーが参加している場合、(カードを一枚も引かずに)1回の手で2枚出る確率はどれくらいでしょうか?
スリーカードポーカーで、(1)クイーンハイ、(2)キングハイ、(3)エースハイのそれぞれの確率をどのように計算しますか?
まずキングハイを計算し、他の 2 つの計算式を簡単に示します。確率は、キングハイのハンドの数をハンドの総数で割ったものになります。キングより小さいランクの数は 11 です。キングハイのハンドには、これらのランクのうち 2 つの異なるランクが必要です。11 個のうち 2 個を配置する方法の数は、 combin (11,2) = 55 です。ただし、これらの組み合わせの 1 つはキング、クイーン、ジャックで、ストレートになるため、その組み合わせを引くと、ストレートを形成しない組み合わせが 54 個残ります。次に、各ランクに 4 つのスーツがあるため、スーツの組み合わせは 4 3 =64 通りあります。ただし、この 64 通りのうち 4 通りはフラッシュになるため、スーツの組み合わせは 64-4=60 通り残ります。したがって、キングハイの組み合わせの総数は 54*60=3240 です。 52枚のカードから3枚を並べる組み合わせは合計で22,100通りあります。したがって、キングハイの確率は3,240/22,100 = 0.1466063です。エースハイの確率は、(combin(12,2)-2)*(4 3 -4)/combin(52,3)=0.1737557です。a-2-3とqkaのストレートの両方があるため、-1ではなく-2であることに注意してください。
クイーンハイの確率は、(combin(10,2)-1)*(4 3 -4)/combin(52,3)=0.119457です。
ロイヤルフラッシュが出る確率はどれくらいですか?シーケンシャルロイヤルフラッシュ(前向きまたは後ろ向き)が出る確率はどれくらいですか?
ロイヤルフラッシュの確率は、ロイヤルフラッシュの可能性のある数(各スーツに1枚ずつ)を、52枚の中から5枚を選ぶ方法の数( combin (52,5) = 2,598,960)で割ったものです。つまり、答えは4/2,598,960 = 0.00000153908、つまり649,740分の1です。
連続ロイヤルフラッシュの確率は、(スーツの数)*(方向の数)/(52枚中5枚のカードの組み合わせの総数)=4*2/ permut (52,5)=8/311,875,200=8/(ロイヤルの数、つまり4(スーツごとに1つ))×ロイヤルフラッシュの方向の数÷52枚中5枚のカードの組み合わせの数、つまりpermut (52,5)=311,875,200で表されます。したがって、答えは4/311,875,200 = 0.00000002565、つまり38,984,400分の1となります。
ドル札でライアーズポーカーをするのが好きです。1枚の紙幣に同じ数字が1、2、3、4、または5つ出る確率はどれくらいですか?ありがとうございます。3人でプレイする場合、数字が1つ出る確率はどれくらいですか?
まず、特定の数字がランダムな紙幣にn回出現する確率について、まだ聞かれていない質問に答えましょう。紙幣には8桁の数字が印刷されているので、特定の数字がn回出現する確率は、combin(8,n)*0.1 n *0.9 8-n /10 8となります。0から8までの特定の数字の出現確率を示す表を以下に示します。
特定の数字のオッズライアーズポーカー
| 番号 | 確率 |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| 合計 | 1.00000000 |
次の表は、あらゆる種類の紙幣の確率を、それぞれのn枚の紙幣の枚数ごとに分類したものです。例えば、シリアル番号66847680には、3枚揃いの紙幣が1枚、ペアが1枚、シングルトンが3枚含まれており、確率は0.1693440です。
ライアーズポーカーにおける一般的な確率
| 8オーク | 7オーク | 6オーク | 5オーク | 4オーク | 3オーク | 2オーク | オーク1本 | 確率 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| 合計 | 1.0000000 | |||||||
オーク = 「一種の」
詳細については、私のLiars Pokerのページを参照してください。
52 枚のカードのデッキでジャックのペアを引く確率はどれくらいでしょうか?
カードを 5 枚引き、すべてのハンドにジャックが 2 枚ずつ含まれると仮定すると、確率は combin(4,2)*combin(48,3)/combin(52,5) = 6*17296/2598960 = 3.99% になります。
パイゴウポーカーでスリーペアが揃う確率はどれくらいですか?スリーオブアカインドよりも確率は低いですか、高いですか?
スリーペアとツーペアを除いた、スリーペアを得る方法と組み合わせの数は次のとおりです。
ワイルドカードなし: combin(13,3)*10*6 3 *4 =2471040
エースのペアに対抗するためにワイルドカードを使用する: combin(12,2)*10*6 2 *4 2 = 380,160
ワイルドカードをシングルトンエースとして使用する: combin(12,3)*6 3 = 47,520
組み合わせの総数は2,898,720通りです。これは、スリーカードの組み合わせ747,0676通りの半分以下です。
あなたの計算式によると、ロイヤルフラッシュのオッズは4/2,598,960 = 1/649,740です。つまり、私がディーラーと1対1でカリビアンスタッドをプレイしていたとしたら、私の手札とディーラーの手札の合計は649,740*2=1,299,480になります。したがって、計算上は1,299,480ハンド後にはロイヤルフラッシュが2つ出るはずです。オッズを正しく理解しているか教えてください。
平均してロイヤルフラッシュは649,740ハンドに1回出現し、1,299,480ハンドではロイヤルフラッシュの期待値は2回であることはご指摘の通りです。しかし、これはあくまで平均です。ハンドを重ねるごとにロイヤルフラッシュに近づくわけではありません。独立した試行のゲームには必ずこの記憶のない性質があるため、ロイヤルフラッシュが出現する時期が遅れることはありません。
1,299,480 ハンド中、ロイヤルがゼロになる確率は 13.53% です。
こんにちは。私はパイゴウポーカーを定期的にプレイしています。このサイトにはゲームに関する素晴らしい情報がたくさんあることに気づきました。先日、友人とプレイしていた時、彼に9ハイのハンドが配られました。これはおそらく最も低いハンドだと思います。私がこのゲームをプレイしてきた中で、このようなハンドは一度しか見たことがありませんでした。それから5ハンド後に、彼は全く同じハンド(2-3-4-5-7-8-9)を配りました。私たちは信じられず、このようなことが起こる確率はどれくらいなのか気になり、このサイトに問い合わせることにしました。貴重なお時間をいただき、また素晴らしいサイトをご利用いただき、ありがとうございます。
9ハイハンドを形成するためのランクの並び方は2通りあります。あなたがおっしゃった方法と、2-3-4-6-7-8-9です。フラッシュを形成しないスーツの組み合わせの数は、4 7 -4*(combin(7,5)*3^2+6*3+1) = 15,552です。したがって、9ハイハンドの確率は2*15,552/combin(53,7) = 31,104/154,143,080、つまり9,911分の1です。もし5回プレイしたとしたら、9ハイハンドが2回出る確率は9,826,685分の1になります。これは偶然の一致であり、乱数生成器やプログラムのコーディングの不具合によるものではないと考えています。
質問は、カジノナイアガラルール(レイズ時に3倍の配当、元の賭け金は失われる)のカジノウォーにおけるハウスエッジとリスク要素の計算についてです。これらの数字はどのようにして算出されたのでしょうか?現在計算中ですが、うまくいきません。ご協力ありがとうございます。
デッキの数をdとします。第1ラウンドで引き分けになる確率は(4*d-1)/(52*d-1)= 0.073955です。第2ラウンドで引き分けになる確率は、12*4*d/(52*d-2)*(4*d-1)/(52*d-3)+(4*d-2)/(52*d-2)*(4*d-3)/(52*d-3) = 0.073974です。第1ラウンドで引き分けになる確率をp 1 、第2ラウンドで引き分けになる確率をp 2とします。すると、プレイヤーのリターンはp 1 *(2*p 2 +(1-p 2 )/2*(1-2))= -0.023301となります。-1を掛けると、ハウスエッジは2.33%となります。あまり急いで説明しなかったことを願います。
カリブ海の組み合わせの総数、19,933,230,517,200はどのようにして導き出されたのでしょうか?5枚のカードを使ったポーカーの組み合わせを参考に、2,598,960という数字を導き出しました。そこから先はどうすればよいのでしょうか?よろしくお願いします。
プレイヤーの組み合わせの数は、 combin (52,5)=2,598,960と正しく計算されています。ディーラーのハンドは、combin(47,5)=1,533,939通りあります。ディーラーのカードは5枚のうち1枚が表向きになる可能性があり、2,598,960*1,533,959*5=19,933,230,517,200通りになります。
まず最初に、あなたのウェブサイトは本当に素晴らしいと思います。何人かに話したのですが、彼らにも試してもらいたいと思っています。これからも成功をお祈りしています。WinPokerへのリンクも気に入りました。WinPokerは気に入ったので注文しました。これは素晴らしいプログラムです。質問があり、あなたが助けてくれることを願っています。セブンカードスタッドの各ハンドの出現回数を計算しようとしています。あなたのセブンカードテーブルのコピーを持っているのですが、その数字を導き出す数学的な方法に興味があります。5枚のカードの数字は計算できるのですが、7枚のカードとなると全く理解できません。私が計算した数字をExcel 2000ファイルで送りたいと思っています。また、ジョーカー付きの53枚のカードのデッキでストレートの数を計算する方法も知りたいです。助けてください!!!!
親切なお言葉ありがとうございます。セブンカードスタッドの数字の計算は難しいですね。だからこそ、私はコンピューターで計算しています。私のプログラムは、あらゆる組み合わせを網羅し、それぞれに点数をつけています。パイゴウポーカーのワイルドストレートの数は、11*(4 4 -4)+10*3*(4 4 -4)=10332です。これにナチュラルストレートの10200個を加えると、合計は20532個になります。
カリビアンスタッドポーカーやレットイットライドのテーブルで、ロイヤルやストレートフラッシュが配られる確率とその算出方法は理解しています。しかし、疑問があります。ゲームを観戦している第三者として、特定のディールにおいて、テーブルにいるプレイヤーにこれらのハンドが配られる確率はどれくらいなのでしょうか?おそらく、プレイ中のハンドの数によって決まるのでしょう…単に個人のオッズ×プレイ中のハンド数なのでしょうか?例えば、4人のプレイヤーがテーブルにいる場合、特定のハンドでロイヤルが配られるということは、ロイヤルのオッズが4倍になるということでしょうか?少し理解に苦しみます!
あなたの方法は良い近似値です。しかし、その論理に従うと、コインを投げた場合、3人中少なくとも1人が表が出る確率は3*50%=150%になります。独立した事象を仮定すると、n回の試行で少なくとも1回成功する確率(各成功確率をpとした場合)は1-(1-p) nです。コイン投げの例の場合、これは1-.5 3 =0.875になります。カリビアンスタッドポーカーを4人でプレイする場合、少なくとも1回ロイヤルフラッシュが出る確率は1-(1-4/2598960) 4 = 0.00000615629になります。しかし、すべてのカードは同じデッキから配られるため、これらの事象は独立ではありません。正確な正解を求めるには数学的に非常に複雑な計算が必要であり、近似値は正解に非常に近いものになるはずです。
パイゴウポーカーでナチュラル7カードストレートフラッシュが出る確率はどれくらいですか?私はカジノで働いていますが、15年ぶりにこの状況を見ました。幸運な客が4万ドルを獲得しました。
ナチュラルストレートフラッシュは32通りあります(4ランク×7枚のカードの8通り)。53枚の中から7枚のカードが出てくる可能性は、combin(53,7) = 154143080通りあります。つまり、答えは32/154143080、つまり4816971分の1です。
スリーカードポーカーで、2 つのハンド連続で 2 つの同じストレート フラッシュ (ランクとスーツの両方) が出る確率はどれくらいですか?
最初のハンドでストレートフラッシュが出る確率は、4*12/combin(52,3) = 48/22100 = 約0.0022です。次のハンドで全く同じ結果になる確率は1/22100です。したがって、答えは(48/22100)*(1/22100) = 48/488410000となり、10,175,208分の1の確率となります。これは、6/49の宝くじに当たる確率(13983816分の1)よりも1.37倍高い確率です。
8デッキのバカラにて、プレイヤーとバンカーの両方が同じ取引下でエースと8のダイアモンドを獲得する確率はどれくらいですか?
(82/combin(416,2))* (72/combin(414,2)) = 0.00000043, or 1 in 2308093
最近、奇妙な出来事を目撃しました。5カードドローポーカーを観戦していた時のことです。最大2枚しかカードを引くことができません。あるプレイヤーが1枚カードを引いてハートのフラッシュを完成させました。ディーラーも1枚カードを引いてスペードのフラッシュを完成させました。当然、ディーラーのフラッシュの方が強いです。このゲームには他に3人のプレイヤーがいました。同じハンドで2つのフラッシュが完成する確率はどれくらいでしょうか?
配られたカードが1枚の場合、または4枚のフラッシュカードを引く場合のフラッシュの確率を定義しましょう。説明を簡単にするために、プレイヤーが4枚のストレートカードでパットペアまたはストレートカードを引くと仮定します。配られたカードでフラッシュが完成する確率(ストレート/ロイヤルフラッシュを除く)は、4*(combin(13,5)-10)/combin(52,5) = 5108/2598960 = 0.0019654です。4枚のフラッシュカードが配られる確率は、4*3*combin(13,4)*13/combin(52,5) = 111540/2598960 = 0.0429172です。ドローでフラッシュが完成する確率は9/47です。したがって、4枚のフラッシュが完成する確率は0.0429172*(9/47) = 0.0082182です。つまり、フラッシュが完成する確率は0.0019654 + 0.0082182 = 0.0101836です。5人中2人がフラッシュを完成させる確率は、combin(5,2)* 0.0101836 2 *(1-0.0101836) 3 = 0.001006、つまり約994分の1です。
5人のプレイヤーと1組のカードで7カードスタッドをプレイした際に、誰かが4枚の同じカードを引く確率を知りたいです。ご協力いただけると幸いです。お時間いただきありがとうございました。
52枚のカードから7枚のカードを選ぶ方法は、combin(52,7)=133,784,560通りあります。フォー・オブ・ア・カインドを含む7枚のカードの組み合わせの数は、13*combin(48,3) = 224,848通りです。13はフォー・オブ・ア・カインドが何段あるか、combin(48,3)は残りの48枚から3枚のカードを選ぶ方法の数です。したがって、確率は224,848/133,784,560 = 0.0017、つまり595分の1となります。
新しいカードのデッキを開くと、各スートのカードはエースからキングまで揃っています。シャッフルされたデッキを、元のエースからキングまでの状態に戻す確率はどれくらいでしょうか?
52 分の 1 の階乗、または 80,658,175,170,943,900,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 分の 1 です。
10 人のプレイヤーにそれぞれ 1 つのデッキから 2 枚のカードが配られた場合、2 人のプレイヤーがエースのペアを出す確率はどれくらいでしょうか。
まず、10人中2人のプレイヤーを選ぶ方法は10*9/2=45通りあります。特定の2人がエースを4枚揃える確率は1/combin(52,4)=1/270725です。つまり、任意の2人がエースのペアを揃える確率は45/270725=0.0001662です。
7 人のプレイヤーがそれぞれ 7 枚のカードを受け取る場合、少なくとも 1 人が 7 枚のフラッシュを受け取る確率はどれくらいでしょうか。
1 人のプレイヤーが 7 枚のフラッシュを獲得する確率は、4 * combin(13,7)/combin(52,7) = 1949 分の 1 です。7 人のプレイヤーのうち少なくとも 1 人が 7 枚のフラッシュを獲得する確率は、約 2785 分の 1 です。
数学的には何でもあり得ることは分かっていますが、先日カジノで10億分の1の確率で起こるような出来事を目撃しました。もちろん、そんな出来事が起こらないというわけではありませんが。何が起こったかご説明しましょう。レット・イット・ライドのテーブルで40ハンド(5人のプレイヤーで約8ラウンド、3枚のカードを40回ずつ配る)の間に、フォー・オブ・ア・カインドが3枚配られました。フォー・オブ・ア・カインドは約4100分の1ですが、40回のハンドで3枚が配られる確率はどれくらいでしょうか? 答えてください。本当に困っています。長年のファンです。
単純化のため、各ハンドは新しいデッキから配られると仮定しましょう。フォー・オブ・ア・カインドが揃う確率は13*48/combin(52,5) = 624/2598960です。40枚のフォー・オブ・ア・カインドのうち3枚だけ揃う確率は、combin(40,3)*p 3 *(1-p) 37 = 7378135分の1(p = 624/2598960)です。つまり、700万分の1の確率に近いと言えます。
まず、あなたのウェブサイトをどれだけ愛しているか、そしてあなたの数学のスキルに感心しているかをお伝えしたかったのです。私はブラックジャックを6デッキで配り、ジョーカーを3枚追加しました。理由はここでは割愛しますが、ジョーカーを3枚連続でプレイヤーに配る確率はどれくらいでしょうか?ありがとうございます。
どういたしまして。褒めていただきありがとうございます。6デッキのシュー(プラス3枚のジョーカー)からジョーカーが3枚連続で配られる確率は、1/combin(315,3) = 5,159,805分の1です。別の解は(3/315)*(2/314)*(1/313)です。
52枚のカードデッキを使って4人のプレイヤーにそれぞれ13枚のカードを配り、4人全員がエースから2までのストレートを持っている場合、その確率はどれくらいでしょうか?カードは同じスーツである必要はありません。
答えは、(4 13 /COMBIN(52,13))* (3 13 /COMBIN(39,13))* (2 13 /COMBIN(26,13)) = 61,204,166,001分の1です。
ロイヤルに 4 枚配られる確率はどれくらいですか?
ロイヤルのスーツは4種類あります。5種類のカードが欠けている可能性があります。5枚目のカードは、他の47枚のカードのいずれかです。つまり、ロイヤルに4枚揃う方法は4×5×47=940通りあります。合計の組み合わせは、(52,5)=2,598,960通りです。つまり、確率は940/2,598,960=2,765分の1です。
ウィズさん、52枚のカードをシャッフルし、その中からランダムに18枚を引いて、3枚ずつ6つの山に分けたとします。山の1つに(4枚のうち)ちょうど3枚のエースが入っている確率はどれくらいでしょうか?
この問題を簡単に解く方法は、最初の山札にエースが3枚ある確率は(4/52)*(3/51)*(2/50) = 1/5525であるということです。しかし、各山札にエースが3枚ある確率は等しいので、6を掛けて6/5525 = 0.001086となります。
ファイブカードスタッドですべての絵札が出る確率はどれくらいですか?
(12/52)*(11/51)*(10/50)*(9/49)*(8/48) = 0.00030474、つまり約3282分の1です。
「Let it Ride」を 2 時間以内にプレイして、4 種類のカードが 2 つ揃う確率はどれくらいでしょうか?
どのハンドでもフォー・オブ・ア・カインドが揃う確率は、13*48/combin(52,5) = 0.0002401です。2時間で120ハンドプレイできると仮定しましょう。フォー・オブ・ア・カインドがちょうど2つ揃う確率は、combin(120,2) × 0.0002401 2 × (1-0.0002401) 118 = 0.000400095 = 2499.41分の1となります。
4 カード ポーカーでは、ストレートとフラッシュのどちらになる可能性が高いですか?
ストレートフラッシュとロイヤルフラッシュを除くと、ストレートの確率は1.02%、フラッシュの確率は1.04%です。つまり、フラッシュの方がわずかに確率が高いということです。
100万ハンド中、ロイヤルフラッシュが出ない状態が20万ハンド続く確率はどれくらいでしょうか?答えそのものよりも、その解決策に興味があります。
普段はこうは言いませんが、何時間も試してみたものの、この問題の計算はどうしても理解できませんでした。そこで、友人であり数学教授でもあるガボール・メジェシに頼りました。彼が教えてくれた「干ばつ」問題用の公式がこちらです。
- 与えられたハンドで勝つ確率を p とします。
- 干ばつの長さを d とします。
- プレイしたハンドの数を n とします。
- k=dp、x=np と設定します。
- k=1 の場合は a=-1 とし、それ以外の場合は k=-ln(-a)/(1+a) となる a を求めます。(a は負の数で、k>1 の場合は -1 < a < 0、k < 1 の場合は a < -1 となり、a は高精度で計算する必要があります。) [ウィザードの注記: この種のソリューションは、Excel のツール メニューのゴール シーク機能を使用して簡単に見つけることができます。]
- k=1の場合はA=2とし、それ以外の場合はA=(1+a)/(1+ak)とする。
- nハンドで長さdの干ばつが発生しない確率は、およそAe a xです。
この問題では、p=1/40391、d=200000、n=1000000、k=4.9516、x=24.758、a=-0.0073337、A=1.03007です。したがって、干ばつが発生しない確率は1.03007*e -0.0073337*24.758 = 0.859042です。したがって、少なくとも1回の干ばつが発生する確率は1-0.859042 = 0.140958です。
Gabor Megyesi氏による5ページにわたる完全な解答(PDF)はこちらです。ご協力ありがとうございました、Gáborさん。
100万回の手札を32,095セットランダムにシミュレーションしました。少なくとも1回は干ばつに見舞われたのは4558セットで、確率は14.20%でした。
異なるデッキから5枚のカードが2つ配られたとします。Aの手札には少なくとも1枚のエースが含まれています。Bの手札にはスペードのエースが含まれています。どちらの手札に、さらに1枚以上のエースが含まれている可能性が高いでしょうか?
次の表は、完全にランダムなハンドで 0 から 4 枚のエースが出る確率を示しています。
エースの確率 — ランダムハンド
| エース | 式 | 組み合わせ | 確率 |
|---|---|---|---|
| 0 | コンビン(48,5) | 1712304 | 0.658842 |
| 1 | コンビン(4,1)×コンビン(48,4) | 778320 | 0.299474 |
| 2 | コンビン(4,2)×コンビン(48,3) | 103776 | 0.03993 |
| 3 | コンビン(4,3)×コンビン(48,2) | 4512 | 0.001736 |
| 4 | 組み合わせ(4,4)×組み合わせ(48,1) | 48 | 0.000018 |
| 合計 | 2598960 | 1 |
1枚から4枚のエースの合計を取ると、少なくとも1枚のエースが出る確率は0.341158です。2枚以上のエースが出る確率は0.041684です。
少なくとも 1 枚のエースがある場合に、少なくとも 1 枚のエースがある確率は、ベイズの定理に従って、確率 (少なくとも 1 枚のエースがある場合に、さらに 2 枚のエースがある) = 確率 (2 枚以上のエース)/確率 (少なくとも 1 枚のエース) = 0.041684/ 0.341158 = 0.122185 と言い換えることができます。
ベイズの定理がまだ錆び付いている人のために説明すると、これは、B が与えられた場合の A の確率は、A と B の確率を B の確率で割った値に等しい、つまり Pr(A が与えられた場合の B) = Pr(A と B)/Pr(B) であることを意味します。
次の表は、スペードのエースをデッキから除いた場合に、他のエースの各数の組み合わせと確率を示しています。
エースの確率 — エースが取り除かれた手
| エース | 式 | 組み合わせ | 確率 |
|---|---|---|---|
| 0 | 組み合わせ(3,0)×組み合わせ(48,4) | 194580 | 0.778631 |
| 1 | コンビン(3,1)×コンビン(48,3) | 51888 | 0.207635 |
| 2 | 組み合わせ(3,2)×組み合わせ(48,2) | 3384 | 0.013541 |
| 3 | 組み合わせ(3,3)×組み合わせ(48,1) | 48 | 0.000192 |
| 合計 | 249900 | 1 |
これは、少なくとももう 1 枚のエースが出る確率が 0.221369 であることを示しています。
面白半分に、ベイズの定理を使って同じ問題を解いてみましょう。スペードのエースが見つかるまでランダムに手札が配られると仮定します。手札にスペードのエースが含まれている場合、少なくとも1枚のエースがさらに出ている確率は、確率(スペードのエースが含まれている場合、少なくとも2枚のエースが手札にある)と書き直すことができます。ベイズの定理によれば、これは確率(手札にスペードのエースと少なくとももう1枚のエースが含まれている)/確率(手札にスペードのエースが含まれている)に等しくなります。分子を確率(スペードのエースを含む2枚のエース)+確率(スペードのエースを含む3枚のエース)+確率(4枚のエース)に分解できます。最初の表を使うと、0.039930×(2/4) + 0.001736×(3/4) + 0.000018 = 0.021285となります。スペードのエースが出る確率は 5/52 = 0.096154 です。つまり、スペードのエースが2枚以上出た場合、少なくとも2枚のエースが出る確率は 0.021285/0.096154 = 0.221369 です。
したがって、少なくとも 1 つのエースがある場合に 2 つ以上のエースが出る確率は 12.22% であり、スペードのエースがある場合に 22.14% となります。
分かりました。あなたの数字は信じますが、それでもまだ納得できません。確率は等しくなるはずです。1枚のエースが配られるのに、スートの違いで何か違いがあるのでしょうか?
もっと単純な状況を考えてみましょう。女性Aが「私には子供が2人いて、少なくとも1人は男の子です」と言い、女性Bが「私には子供が2人いて、上の子はジョンという名前です」と言うとします。ジョンという名前の子供は女の子ではなく、同じ名前を複数の子供に付ける女性もいないと仮定します。条件付き確率を用いると、女性Aの子供が2人とも男の子である確率は、pr(2人とも男の子)/pr(少なくとも1人の男の子) = pr(2人とも男の子)/(1-pr(2人とも女の子)) = (1/4)/(1-(1/4)) = (1/4)/(3/4) = 1/3となります。しかし、女性Bの下の子供が男の子である確率、あるいは2人とも男の子である確率は?です。なぜなら、上の子供の名前がジョンであると言っても、下の子供については何も分からないからです。
別の例として、Jiffy Lube に行って、同じ価格で 2 つのプランを提示されたとします。プラン A は、4 つの部品を検査し、最初に不良品が見つかったものだけを交換するというものです。プラン B は、1 つの問題だけを検査し、見つかった場合は修理するというものです。プラン A を選びませんか? 車に持ち込まれた不良部品の数は予想と同じですが、プラン A の方が問題が見つかる確率が高くなるため、そのプランでは不良品の数は少なくなります。同様に、エースを検査するとおそらくエースだけが出てきますが、スペードのエースを検査すると他の 3 つのスーツは検査されないため、エースである可能性が高くなります。
フォーカードポーカーで 5 枚中 4 枚のカードを使ったストレートフラッシュの数が 2072 という数字にどうやって辿り着いたのですか?
まずストレート フラッシュを、同じスーツのカードが 4 枚連続するものと、5 枚連続するものの 2 種類に分けました。5 枚のストレート フラッシュの数は、スーツの数 * スパンの数 (エースから 10 までの最下位カード) = 4 * 10 = 40 です。4 枚のストレート フラッシュには、11 種類のスパン (エースからジャックまでの最下位カード) があります。A234 および JQKA のストレート フラッシュの場合、5 枚目のカードは 47 種類 (52 から、すでに取り除かれた 4 枚と、すでに計算されている 5 枚のストレート フラッシュを形成する 5 枚目のカードを引いたもの) のいずれかになります。したがって、スパン A234 または JQKA のストレート フラッシュは、4 * 2 * 47 = 376 種類あります。他の 9 種類のうち、5 枚目のカードになり得るカードは 46 種類 (52 から、すでに取り除かれた 4 枚と、5 枚のストレート フラッシュを形成する 2 枚を引いたもの) です。したがって、スパン2345からTJQKまでのストレートフラッシュの数は4*9*46=1656です。つまり、4枚のストレートフラッシュの合計数は40+376+1656=2072です。
17枚目のカードが配られたら、どんな状況でもフラッシュが100%成立する可能性があります。何枚目のカードが配られたら、ストレートが100%成立するのでしょうか?
ストレートは45枚のカードでのみ成立します。例えば、A、2、3、4、6、7、8、9、J、Q、Kをすべて合計44枚配っても、ストレートは成立しません。
素晴らしいオッズの魔法使い様、あなたの統計的洞察力には本当に驚嘆しております。もしよろしければ、セブンカードスタッドでセブンカードストレート(A、2、3、4、5、6、7、または2、3、4、5、6、7、8、または7、8、9、10、ジャック、クイーン、キング)の確率を計算していただけないでしょうか。これはポーカーの役ではないことは承知していますが、プレイ中にふとこの話が出て、セブンカードスタッドで通常のフルハウスよりも確率が低いのではないかと疑問に思いました。ありがとうございます、知識豊富な方。
こんなに優しく誘ってくれて、どうやって断ればいいの?まず、52枚のカードから順番に関係なく7枚を選ぶ方法は、 combin (52,7) = 133,784,560通りあります。7枚のストレートは8通りのスパン(最下位カードはAから8まで)があります。もし7つの異なるランクがあるとしたら、スートの並び方は4 7 = 16384通りあります。これには同じスートのカードも含まれ、ストレートフラッシュになります。つまり、確率は8*16,384/133,784,560 = 1020.6952分の1です。
1 つのデッキから 4 枚のカードを配った場合、少なくとも 1 枚のカードがスペードである確率はどれくらいですか。
スペードが0枚の確率は(39/52)*(38/51)*(37/50)*(36/49) = 0.303818です。したがって、少なくとも1枚のスペードが出る確率は1-0.303818 = 0.696182です。
シングルデッキゲームで、4枚のカードのうち少なくとも1枚はエースとデュースになる確率はどれくらいでしょうか?これはオマハゲームで知っておくと役立ちます。
確率101から、Pr(AまたはB) = Pr(A) + Pr(B) - Pr(AとB) であることがわかります。つまり、Pr(AとB) = Pr(A) + Pr(B) - Pr(AまたはB) です。Aがエース、Bがデュースを出した場合を考えてみましょう。Pr(A) = Pr(少なくとも1枚のエース) = 1 - Pr(エースなし) = 1 - combin(48,4) / combin (52,4) = 1 - 0.7187 = 0.2813 です。デュースが出ない確率も当然同じです。同じ論理で、pr(AまたはB) = Pr(少なくとも1枚のエースまたは2) = 1-Pr(エースも2枚もない) = 1-combin(44,4)/combin(52,4) = 1 - 0.501435 = 0.498565となります。したがって、少なくとも1枚のエースと2枚が出る確率は0.2813 + 0.2813 - 0.498565 = 0.063962となります。
6 枚のカードのゲームで、ダイヤのジャックが 27 回連続で配られる確率はどれくらいでしょうか?
1回のハンドでこの数字が出る確率は6/52です。27回連続でこの数字が出る確率は(6/52) 27 = 20,989,713,842,161,800,000,000,000分の1です。
「デッドマンズハンド」、つまりエースと8のツーペアが出る確率はどれくらいでしょうか?
各ペアの4つのスーツのうち2つを組み合わせると、6通りの並べ方があります。シングルトンカードは44枚あります。したがって、成立する組み合わせの数は6×6×44 = 1584通りです。合計で2,598,960通りの組み合わせがあるので、確率は0.0609%です。
まさにその手札を得る方法は一つしかありません。つまり、その確率はcombin(52,5)で1、つまり2,598,960分の1となります。
標準的な52枚のカードデッキから配られる可能性のある5枚のカードのうち、重複していない1枚のカードのスーツがジェネリックとみなされる各ハンドのオッズ/確率はどれくらいでしょうか?例えば、A♠ A♣ Aというハンドを考えてみましょう。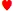 あ
あ 2. このハンドでは、2のスーツは無視され、デッキにある4枚の2のいずれかを表します。別の例としては、AJ-8-6-5があります。このハンドでは、5枚のカードすべてのスーツは無視され、このような組み合わせは1つしか起こりません。別の例としては、3♠ 3があります。
2. このハンドでは、2のスーツは無視され、デッキにある4枚の2のいずれかを表します。別の例としては、AJ-8-6-5があります。このハンドでは、5枚のカードすべてのスーツは無視され、このような組み合わせは1つしか起こりません。別の例としては、3♠ 3があります。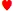 7♣ 7♠ Q。このハンドでは、2枚の3と2枚の4のスートは無視されません。なぜなら、ハンドには複数のスートがあるからです。しかし、Qのスートは汎用です。つまり、ハンドに重複していないカードのスートは無視され、そのハンドは可能性のあるハンドの1つとみなされます。ただし、各カードのスートを無視しなければ、同じハンドが何度も出現する可能性はあります。つまり、特定の5枚のカード、例えばQで構成されるストレートまたはフラッシュです。
7♣ 7♠ Q。このハンドでは、2枚の3と2枚の4のスートは無視されません。なぜなら、ハンドには複数のスートがあるからです。しかし、Qのスートは汎用です。つまり、ハンドに重複していないカードのスートは無視され、そのハンドは可能性のあるハンドの1つとみなされます。ただし、各カードのスートを無視しなければ、同じハンドが何度も出現する可能性はあります。つまり、特定の5枚のカード、例えばQで構成されるストレートまたはフラッシュです。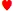 J♣ 10
J♣ 10 9
9 8♠ または A♠ J♠ 8♠ 7♠ 3♠ は、たとえスーツが異なっていても、同じカードの組み合わせは重複となるため、一度しか出現しません。したがって、この基準を用いると、配られるハンドの O/P はいくらになるでしょうか?つまり、標準の52枚のデッキには、このような5枚のハンドがいくつ存在するのでしょうか?ご意見ありがとうございます。
8♠ または A♠ J♠ 8♠ 7♠ 3♠ は、たとえスーツが異なっていても、同じカードの組み合わせは重複となるため、一度しか出現しません。したがって、この基準を用いると、配られるハンドの O/P はいくらになるでしょうか?つまり、標準の52枚のデッキには、このような5枚のハンドがいくつ存在するのでしょうか?ご意見ありがとうございます。
この概念はよく知っています。5枚のカードで構成されたハンドは134,459種類あります。私がこれを知っているのは、私が初めて作ったビデオポーカープログラムで、2,598,960種類ものハンドをすべて分析し、ペイテーブルを一通り確認するのに何日もかかったからです。しかし、134,459種類ものハンドクラスをそれぞれ1つずつ実行し、そのクラスに含まれるハンドの数で重み付けすることで、実行時間を95%も短縮できます。最近私が分析したブラックジャック・ボーナスポーカーのように、スーツが特定のゲームの場合は、古いプログラムを引っ張り出して、ゆっくりとした方法で分析しなければならないこともあります。
4 つのスーツではなく 5 つのスーツを持つデッキを使用したファイブカード スタッドの確率はどれくらいですか?
ファイブスーツポーカーの組み合わせ
| 手 | 組み合わせ | 確率 | 式 |
| 5枚の同じもの | 13 | 0.000002 | 13 |
| ストレートフラッシュ | 50 | 0.000006 | 5*10 |
| フォー・オブ・ア・カインド | 3900 | 0.000472 | 13*12*組み合わせ(5,4)*5 |
| フラッシュ | 6385 | 0.000773 | 5*(組み合わせ(13,5)-10) |
| フルハウス | 15600 | 0.001889 | 13*12*コンバイン(5,3)*コンバイン(5,2) |
| 真っ直ぐ | 31200 | 0.003777 | 10*(5^5-5) |
| スリーオブアカインド | 214500 | 0.025969 | 13*COMBIN(12,2)*COMBIN(5,3)*5^2 |
| 2組 | 429000 | 0.051938 | COMBIN(13,2)*11*COMBIN(5,2)^2*5 |
| ペア | 3575000 | 0.432815 | 13*COMBIN(12,3)*COMBIN(5,3)*5^3 |
| 何もない | 3984240 | 0.48236 | (組み合わせ(13,5)-10)*(5^5-5) |
| 合計 | 8259888 | 1 |
フルハウスとフラッシュの順序を逆にしたことに注意してください。
標準的なトランプの 5 枚のカードの組み合わせのうち、ちょうど 2 つのスーツのカードが含まれたものはいくつありますか?
2つのスーツは4と1、または3と2に分割できます。まずは4/1の分割を見てみましょう。4枚のカードを持つカードには4つのスーツから選ぶことができ、1枚のカードを持つカードには3つのスーツから選ぶことができます。13のランクから4つのランクを選ぶ方法はcombin(13,4)=715通りあります。1つのランクを選ぶ方法は13通りあります。つまり、2つのスーツの間で4/1の分割が発生する方法は4×3×715×13=111,540通りあります。同様の論理で、3/2の分割が発生する方法は4×3×combin(13,3)×combin(13,2)=267,696通りあります。したがって、全体の確率は(111540+267696)/combin(52,5) = 14.59%となります。
2-3-4-5-7のアンスーツカードが配られる確率はどれくらいですか? ありがとうございます!素晴らしいサイトですね!
ありがとう。(4 5 -4)/combin(52,5) = 1020/2598960 = 2,548分の1。
先日フォックスウッズに行って、フォックスウッズ ポーカー クラシックの最後の2つのテーブルを観戦していました。ワールド ポーカー ツアーの司会者の一人、ヴィンス ヴァン パテンが観戦にやって来ると、彼はその場にいたポーカー プロたちとあらゆる種類のプロップベットを始めました。彼は、デッキ全体をめくりながら、エース、2、3、4、…とキングまでカードをめくり、またエースから始めて、宣言したカードが一度も出ないようにできれば、20対1の配当を出すと提案していました。誰も最後までやり遂げられず、ヴィンスは皆が諦めるまでの10分ほどで数百ドルを勝ち取りました。こんなことが起こり得るはずなのに、20対1の配当を出すなんて、ヴィンスが相当なハチャメチャな賭け方をしているんじゃないかと疑っています。デッキ全体をやり遂げられる確率は一体どれくらいなのでしょう?
勝つ確率を推定する簡単な方法は、すべてのカードが12/13の確率で記載されたランクと一致しないと仮定することです。この賭けに勝つには、被害者はこれを52回成功させる必要があります。52回勝つ確率は(12/13) 52 = 1.56%です。妥当な賭け金は63.2対1です。20対1では、ヴィンスは67.3%の優位性があります(痛い!)。
私よりも数学に詳しいGMによると、実際の確率は1.6232727%です。この差が生じる理由は、各ピックの結果が過去のピックと正の相関関係にあるためです。
昨晩プレイしていた時、プレイヤーの一人、ずる賢く、みすぼらしく、攻撃的な老プレイヤーが、フロップでイーブンマネーのサイドベットをしようとテーブルに挑んできました。この気難しい老プレイヤーは、フロップの3枚のカードのうち1枚がエース、デュース、ジャックのいずれかになるかに賭けていました(時には、識別可能な3枚のカードを入れ替えることもありました)。この賭けのオッズはどれくらいでしょうか?賢明な方、ご意見をいただければ幸いです。
カードが全て公開される前、フロップに3つのランクのカードが出現しない確率は、 combin (40,3)/combin(52,3) = 9880/22100 = 44.71%です。つまり、このプレイヤーは10.59%のアドバンテージを持っていました。
52枚のカードから5枚が配られ、最初の1枚がキングだとします。キングが少なくとももう1枚出る確率はどれくらいでしょうか? これと似たエースの問題を解いていたのを見たのですが、よく理解できませんでした。何か助けていただけると嬉しいです。
確率の問題に答える際に私が好んで使うのは、組み合わせ関数を使うことです。この方法では、デッキ内の48枚のキング以外のカードからキング以外の4枚を選ぶ方法は、 combin (48,4) = 194,580通りあります。デッキの残りの51枚のカードから任意の4枚を選ぶ方法は、combin(51,4) = 249,900通りあります。つまり、次の4枚のカードにキングが1枚も含まれない確率は、194,580/249,900 = 77.86%です。したがって、少なくとも1種類のカードが含まれない確率は、100% - 77.86% = 22.14%です。
何人かの方から、このような単純な確率の質問をするタイプの人には、組み合わせ関数は難しすぎるのではないかというご意見をいただきました。私もその意見には同意しますが、このサイトの主目的は読者の皆様に数学について少しでも理解を深めていただくことです。組み合わせ関数は確率論において非常に有用であり、多くの時間を節約してくれます。しかし、今回の問題は組み合わせ関数がなくても簡単に答えられます。
2枚目のカードがキングでない確率は48/51です。これは、デッキにキング以外のカードが48枚残っており、カードの合計が51枚だからです。2枚目のカードがキングでない場合、3枚目のカードもキングでない確率は47/50(キング以外のカード47枚を残り50枚で割る)です。これを最後まで繰り返すと、残りの4枚のカードがすべてキングでない確率は(48/51)×(47/50)×(46/49)×(45/48) = 77.86%となります。そうでない確率、つまり少なくとも1枚のキングである確率は、100% - 77.86% = 22.14%です。
まず、52枚のカードから5枚のカードを選びます。次に、それらのブラックジャックの数字を合計します(T、J、Q、K = 10、A = 1)。合計が偶数/奇数になる確率はどれくらいでしょうか?偶数カードが多すぎるので、合計が偶数になる可能性がはるかに高くなると思います。
驚くべきことに、52枚のカードのうち30枚が偶数であるにもかかわらず、奇数の合計が出る確率は50.03%と、より高くなります。以下の表は、それぞれの偶数/奇数への分割の確率を示しています。
奇数/偶数に関する質問
| イーブン | オッズ | 組み合わせ | 確率 | 和 |
| 0 | 5 | 15504 | 0.005965 | 奇数 |
| 1 | 4 | 155040 | 0.059655 | 平 |
| 2 | 3 | 565440 | 0.217564 | 奇数 |
| 3 | 2 | 942400 | 0.362607 | 平 |
| 4 | 1 | 719200 | 0.276726 | 奇数 |
| 5 | 0 | 201376 | 0.077483 | 平 |
| 合計 | 2598960 | 1 |
デッキから 3 枚のカードを引いたとき、そのうち 1 枚だけがスペードである確率はどれくらいでしょうか。
最初のカードがスペードで、次の2枚がスペードではない確率は、(13/52)×(39/51)×(38/50) = 14.53%です。スペードは3枚のカードのうちどれか1枚である可能性があるため、この値を3倍します。つまり、答えは3×14.53% = 43.59%です。組み合わせ関数を使いたい方は、13×combin(39,2)/ combin (52,3) = 9,633/22,100 = 43.59%となります。
0から1までの(均等に分布する)乱数を2つ選びます。そして、そのうち小さい方を選びます。選んだ数の平均はいくらでしょうか?n個の数値を一般化した場合はどうでしょうか?
数が2つの場合、答えは1/3、n個の場合、答えは1/(n+1)です。数学の問題のページに、問194と問195の解答を掲載しました。
3人が関わるゲームです。(a) あなた自身、(b) 対戦相手、(c) 審判です。各自が0から1までの実数を秘密裏に選びます。すべての数字が選ばれたら、発表します。審判の数字に最も近く、かつその数字を超えなかったプレイヤーが勝ちます。もしあなたが審判の数字に近かった場合、あなたは1ドルを獲得します。もし対戦相手の方が近かった場合、あなたは1ドルを失います。両方のプレイヤーが審判の数字を超えた場合、または同点の場合は、ゲームは引き分けとなります。
相手がランダムに数字を選んだ場合、期待収益を最大化できる数字はありますか?相手にも戦略がある場合はどうでしょうか?
皆さんが喜んでくれることを願っています。後半部分には一日中取り組みましたが、それでも答えは間違っていました。読者の皆さんの喜びを奪ってしまう恐れがあるので、ここで答えをそのまま公開することはしません。この問題は2つの問題に分け、解答と解法をmathproblems.info (問題196と197)に投稿しました。
標準的な 52 枚のカードのデッキからランダムに 5 枚のカードを選んだ場合、4 つのスーツがすべて表される確率はどれくらいでしょうか。
2枚のカードが入ったスーツが1つと、1枚ずつ入ったスーツが3つあります。2回表されるスーツには4つのスーツの可能性があります。2回表されるスーツの場合、13のランクから2つのランクを選ぶ組み合わせは(13,2)=78通りあります。他の3つのスーツの場合、それぞれ13通りのランクが考えられます。したがって、組み合わせの総数は4 × 78 × 13 × 13 × 13 = 685,464通りです。52枚のカードから5つのカードを選ぶ組み合わせは(52,5)=2,598,960通りあります。したがって、確率は685,464/2,598,960 = 26.37%です。
ランダムなカードデッキに、例えばクイーンとキングなど、任意の2つのランクが連続して現れる確率はどれくらいでしょうか?誰かが、それが起こるかどうかに賭け金を等しくして私に賭けようとしました。
ランダムシミュレーションによると、確率は48.64%です。だから、私はその賭けに出たでしょう。
52 枚のカードのデッキから任意の 5 枚のカードを 0 から 2,598,959 までの整数にマッピングする関数を推奨できますか?
はい。まず、各カードに0から51までの値を割り当てます。カードをc1からc5と呼び、c1を最低、c5を最高として並べます。次に、次の関数を呼び出します。
int GetIndex(int c1, int c2, int c3, int c4, int c5)
{
return combin(c5,5) + combin(c4,4)+ combin(c3,3) + combin(c2,2) + combin(c1,1);
}
combin は従来の値を返しますが、最初の値が 2 番目の値より小さい場合を除き、次のように 0 を返します。
int 結合(int x, int y)
{
もし (y>x)
0を返します。
それ以外
{
整数 i,n;
1 の場合
(i=x-y+1; i<=x; i++) の場合
n*=i;
(i=2; i<=y; i++) の場合
n/=i;
n を返します。
}
}
配列要素にアクセスするためにこれを行う場合は、次のように配列をロードします。
カウント=0;
(c5 = 4; c5 < 52; c5++) の場合
{
(c4 = 3; c4 < c5; c4++) の場合
{
(c3 = 2; c3 < c4; c3++) の場合
{
(c2 = 1; c2 < c3; c2++) の場合
{
(c1 = 0; c1 < c2; c1++) の場合
{
index_array[count]=WhateverYouWish;
カウント++;
}
}
}
}
}
10 枚のストレート フラッシュのうち 3 枚を引き、1 つのギャップがあるストレート フラッシュに 3 枚を保持する確率はどれくらいですか。

これは二項分布のような問題です。一般的な公式は、ある事象の確率がpで、それぞれの結果が独立している場合、t回の試行のうち正確にw回発生する確率は、(t,w)×p w ×(1-p) tw となります。
この場合、ストレートフラッシュを作る方法は2通りあります。ダイヤの8と、ダイヤの6またはJのいずれかのカードがもう1枚必要です。デッキに残っている47枚のカードから2枚を引く方法は、combin(47,2)=1,081通りあります。したがって、1回のハンドでストレートフラッシュが完成する確率は、2/1,081 = 0.0018501です。10回中3回ストレートフラッシュが完成する確率は、combin(10,3)×0.0018501 3 ×(1-0.0018501) 7 = 0.000000750178、つまり1,333,017分の1です。
54枚のカード(ジョーカー2枚を含む)を2組シャッフルします。プレイヤーはそのうちの半分を受け取ります。赤の3が4枚すべて出る確率は?
赤い3が4枚と、それ以外のカードが104枚あります。赤い3を4枚全て揃える方法は1つだけです。残りの104枚のうち50枚を揃える方法は、 combin (104,50)= 1.46691 × 10 28 通りあります。組み合わせの総数は、combin(108,54)= 2.48578 × 10 30 です。combin(104,50)/combin(108,54) = 0.059012です。
大きな数字を扱いたくない場合は、別の解決策があります。4枚の赤い3に1から4の番号を付けます。最初の赤い3がプレイヤーの山札にある確率は54/108です。次に、最初の3枚を取り除きます。プレイヤーが2枚目の赤い3を持っている確率は53/107です。これは、プレイヤーの残りカードが53枚で、残りのカードが107枚だからです。同様に、プレイヤーが3枚目の赤い3を持っている確率は52/106、4枚目の赤い3を持っている確率は51/105です。(54/108) × (53/107) × (52/106) × (51/105) = 0.059012。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
面白いですね。先ほども書いたように、あの手の動きはネバダ州のどこででも23.7年に一度くらい起こると推定しています。今回もそのうちの一つだったと言えるでしょう。
例えばキングとクイーンのように、2つのランクを選んだとします。ランダムにシャッフルされた52枚のカードの中で、キングとクイーンが少なくとも1回は隣り合う確率はどれくらいでしょうか?
私の場合は48.6279%です。もし賭けようと思っているなら、「イエス」のオッズは1.0564対1になるでしょう。
最近、ブリッジで「パーフェクト」なゲームがあったと聞きました。各プレイヤーが4つのスーツのうち1つを13枚ずつ配るゲームです。その確率はどれくらいですか?
2011 年にウォリックシャーで行われたホイストのゲームでそれが起こったという噂もあります。他の読者のために、これは 52 枚のカードのデッキを 13 枚ずつの 4 つのグループに分割し、各セットが 1 つのスートの 13 枚のカードだけで構成されている場合の確率がどれくらいかを尋ねています。
52枚のカードを13枚ずつ4組に分ける組み合わせは、combin(52,13)combin(39,13)*combin(26,13) = 53,644,737,765,488,800,000,000,000,000通りあります。4つのスーツを4人のプレイヤーに好きなように分配できるので、4! = 24が勝ちの組み合わせの数になります。したがって、確率は2,235,197,406,895,370,000,000,000,000分の1です。この数字をもう少し具体的に表すと、地球上の75億人全員が1秒に1枚のブリッジのハンドを配ったとすると、50億年後に太陽が爆発する前に誰かがいわゆるパーフェクトハンドを配る確率は16,558分の1になります。
しかし、「完璧な」手札とは、1人のプレイヤーが任意のスートの13枚のカードをすべて揃えることだと定義する人もいます。この確率は39,688,347,497ゲームに1回です。おそらく、地球上のどこかでたまに起こるのでしょう。
テキサス ホールデムで、2 人のプレイヤーが両方ともホールカードを使用して同じ手でフラッシュを完成させる確率はどれくらいですか?
まず、このような状況が発生するプレイヤーカードとボードカードの組み合わせの数を調べてみましょう。スートは4種類あります。すると、与えられたスートから13枚のカードの中から4枚を選ぶ方法は、combin(13,4)=715通りあります。
第二に、これが起こる一つの方法は、プレイヤーが盤上に同じスートのカードを3枚置き、残りの2枚を残りの39枚のカードから選ぶことです。選択したスートの残り9枚のカードのうち3枚が盤上に現れる場合、combin(9,3)=84通りあります。そして、他の3つのスートの残り39枚のカードからさらに2枚を選ぶ場合、combin(39,2)=741通りあります。つまり、盤上に問題のスートのカードが3枚ある場合、84*741=62,244通りあります。
3 つ目は、同じスートのカードが 4 枚ボード上にあり、残りの 1 枚が他の 39 枚のカードの中にある場合です。選択したスートの残りの 9 枚のカードのうち 4 枚がボード上に存在する場合、combin(9,4) = 126 通りの可能性があります。次に、他の 3 つのスートの残りの 39 枚のカードからさらに 1 枚を選ぶ場合、39 通りの可能性があります。ただし、これらすべてが両方のプレイヤーが両方のホールカードを使用することになるわけではありません。その条件を満たすには、問題のスートの最も低いカードがボード上にある必要があります。そのスートの 8 枚のカードのうち、その確率は 4/8 = 1/2 です。したがって、問題のスートのカードが 4 枚ボード上にある場合、126*39*(1/2) = 2,457 通りの可能性があります。
4つ目に、これが起こり得る最後の方法は、プレイヤーがボード上に同じスートのカードを5枚持っている場合です。ボード上に、選択したスートの残り9枚のうち5枚が揃う可能性は、combin(9,5)=126通りあります。しかし、これらすべてが両プレイヤーが両方のホールカードを使う結果になるわけではありません。その条件を満たすには、該当するスートの最低ランクの2枚がボード上になければなりません。そのスートの9枚のカードのうち、その確率は、combin(5,2)/combin(9,2) = 10/36 = 5/18です。つまり、該当するスートのカードが4枚ボード上に揃う可能性は、126*(5/18)=35通りあります。
したがって、これが発生する組み合わせの数は、715 * (62,244 + 2,457 + 35) = 46,286,240 です。
プレイヤーのホールカードとして 52 枚の中から 4 枚のカードを選び、さらにボードに残っている 48 枚の中から 5 枚を選ぶ方法の組み合わせの総数は、combin(52,4)*combin(48,5) = 463,563,500,400 です。
したがって、確率は 46,286,240 / 463,563,500,400 = 0.000399395 = 2,504 分の 1 となります。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されました。
カジノディーラーが新しいスリーカードポーカーのバリエーションに取り組んでいます。彼女は標準デッキからすべての絵札を取り、よくシャッフルします。そして、プレイヤー1に3枚、プレイヤー2に3枚、プレイヤー3に3枚、そして最後の3枚をプレイヤー4に配ります。4つのハンド全てにストレート(どのスートのJQK)が含まれる確率はどれくらいでしょうか?
一度に1人のプレイヤーにカードを配ります。最初のプレイヤーが各ランクのカードを1枚ずつ受け取る確率は、4^3/combin(12,3) = 64/220です。
最初のプレイヤーがストレートを出したと仮定すると、各ランクのカードが3枚ずつ残ったデッキが空になります。2番目のプレイヤーが各ランクのカードを1枚ずつ出す確率は、3^3/combin(9,3) = 27/84です。
最初の2人のプレイヤーがストレートを出したと仮定すると、各ランクのカードが2枚ずつ残ったデッキが空になります。3人目のプレイヤーが各ランクのカードを1枚ずつ出す確率は、2^3/combin(6,3) = 8/20です。
最初の3人がストレートを作ったと仮定すると、各ランクのカードが1枚ずつ残ったデッキが空になります。この3枚のカードは明らかにストレートを形成します。
したがって、4 人のプレイヤー全員がストレートになる確率は、(64/220)*(27/84)*(8/20)*1 = 216/5775 = 72/1925 = 3.74% となります。
この質問は、 この投稿から始まり、Wizard of Vegas の私のフォーラムで尋ねられ、議論されています。
48枚のカードデッキがあり、4つのスーツがあり、各スーツに12枚のカードがあるとします。15枚のカードを引いた場合、各スーツに少なくとも1枚はカードを引く確率はどれくらいでしょうか?
まずは 100% から始めて、4 つ未満のスーツになる確率を差し引きます。
例えば、48枚のカードにハートが1枚も含まれていない確率はどれくらいでしょうか?ハートではないカードは36枚あります。36枚の中から15枚を選ぶ方法はcombin(36,15) = 5,567,902,560通りです。48枚の中から15枚を選ぶ方法は1,093,260,079,344通りです。つまり、ハートが15枚含まれていない確率は5,567,902,560 / 1,093,260,079,344 = 0.005093となります。
次に、これを 4 倍にして、ハートだけでなく、どのスーツも見逃す確率を求めます。4 × combin(36,15)/combin(48,15) = 0.02037174。
しかし、この方法では状況によっては二重カウントされてしまいます。例えば、黒いカードが15枚あるとします。この場合、ハートとダイヤの両方が除外され、二重カウントされてしまいます。そのため、この状況を修正する必要があります。4つのスーツから2つのスーツを選ぶ方法はcombin(4,2) = 6通りあります。15枚のカードすべてが特定の2つのスーツである確率は、combin(24,15)/combin(48,15) = 1307504/1,093,260,079,344 = 0.00000120です。前述のように、4つのスーツから2つのスーツを選ぶ方法は6通りあるため、すべてのカードが2つのスーツになる方法は、6 × combin(24,15)/combin(48,15) = 0.00000718通りです。
二重に数えたものを差し引くと、2 つまたは 3 つのスーツが表される確率は 0.02037174 - 0.00000718 = 0.02036456 になります。
12 枚の中から 15 枚のカードを選択することは不可能なので、1 つのスーツが表されることを心配する必要はないことに注意してください。
最後のステップとして、2 つまたは 3 つのスーツの確率を 100% から引いて、4 つのスーツすべてが表される確率を算出します: 1.00000000 - 0.02037174 = 0.97963544。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
シャッフルされた(ランダムであると想定される)カードのデッキから 13 枚のカードを配る場合、いくつの異なるランクが表示されると予想されますか?
これは、まさにマルコフ連鎖のような問題です。
次の表は、配られたカードの枚数が 1 から 52 までのすべての場合における、0 から 4 のカードのランクの予想数を示しています。
配られたカードによる予想ランク
| カード | 0 ランク | 1位 | 2ランク | 3つのランク | 4つのランク | 期待される ランク |
|---|---|---|---|---|---|---|
| 1 | 12.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| 2 | 11.058824 | 1.882353 | 0.058824 | 0.000000 | 0.000000 | 1.941176 |
| 3 | 10.174118 | 2.654118 | 0.169412 | 0.002353 | 0.000000 | 2.825882 |
| 4 | 9.343577 | 3.322161 | 0.324994 | 0.009220 | 0.000048 | 3.656423 |
| 5 | 8.564946 | 3.893157 | 0.519088 | 0.022569 | 0.000240 | 4.435054 |
| 6 | 7.836014 | 4.373589 | 0.745498 | 0.044178 | 0.000720 | 5.163986 |
| 7 | 7.154622 | 4.769748 | 0.998319 | 0.075630 | 0.001681 | 5.845378 |
| 8 | 6.518655 | 5.087731 | 1.271933 | 0.118319 | 0.003361 | 6.481345 |
| 9 | 5.926050 | 5.333445 | 1.561008 | 0.173445 | 0.006050 | 7.073950 |
| 10 | 5.374790 | 5.512605 | 1.860504 | 0.242017 | 0.010084 | 7.625210 |
| 11 | 4.862905 | 5.630732 | 2.165666 | 0.324850 | 0.015846 | 8.137095 |
| 12 | 4.388475 | 5.693157 | 2.472029 | 0.422569 | 0.023770 | 8.611525 |
| 13 | 3.949628 | 5.705018 | 2.775414 | 0.535606 | 0.034334 | 9.050372 |
| 14 | 3.544538 | 5.671261 | 3.071933 | 0.664202 | 0.048067 | 9.455462 |
| 15 | 3.171429 | 5.596639 | 3.357983 | 0.808403 | 0.065546 | 9.828571 |
| 16 | 2.828571 | 5.485714 | 3.630252 | 0.968067 | 0.087395 | 10.171429 |
| 17 | 2.514286 | 5.342857 | 3.885714 | 1.142857 | 0.114286 | 10.485714 |
| 18 | 2.226939 | 5.172245 | 4.121633 | 1.332245 | 0.146939 | 10.773061 |
| 19 | 1.964946 | 4.977863 | 4.335558 | 1.535510 | 0.186122 | 11.035054 |
| 20 | 1.726771 | 4.763505 | 4.525330 | 1.751741 | 0.232653 | 11.273229 |
| 21 | 1.510924 | 4.532773 | 4.689076 | 1.979832 | 0.287395 | 11.489076 |
| 22 | 1.315966 | 4.289076 | 4.825210 | 2.218487 | 0.351261 | 11.684034 |
| 23 | 1.140504 | 4.035630 | 4.932437 | 2.466218 | 0.425210 | 11.859496 |
| 24 | 0.983193 | 3.775462 | 5.009748 | 2.721345 | 0.510252 | 12.016807 |
| 25 | 0.842737 | 3.511405 | 5.056423 | 2.981993 | 0.607443 | 12.157263 |
| 26 | 0.717887 | 3.246098 | 5.072029 | 3.246098 | 0.717887 | 12.282113 |
| 27 | 0.607443 | 2.981993 | 5.056423 | 3.511405 | 0.842737 | 12.392557 |
| 28 | 0.510252 | 2.721345 | 5.009748 | 3.775462 | 0.983193 | 12.489748 |
| 29 | 0.425210 | 2.466218 | 4.932437 | 4.035630 | 1.140504 | 12.574790 |
| 30 | 0.351261 | 2.218487 | 4.825210 | 4.289076 | 1.315966 | 12.648739 |
| 31 | 0.287395 | 1.979832 | 4.689076 | 4.532773 | 1.510924 | 12.712605 |
| 32 | 0.232653 | 1.751741 | 4.525330 | 4.763505 | 1.726771 | 12.767347 |
| 33 | 0.186122 | 1.535510 | 4.335558 | 4.977863 | 1.964946 | 12.813878 |
| 34 | 0.146939 | 1.332245 | 4.121633 | 5.172245 | 2.226939 | 12.853061 |
| 35 | 0.114286 | 1.142857 | 3.885714 | 5.342857 | 2.514286 | 12.885714 |
| 36 | 0.087395 | 0.968067 | 3.630252 | 5.485714 | 2.828571 | 12.912605 |
| 37 | 0.065546 | 0.808403 | 3.357983 | 5.596639 | 3.171429 | 12.934454 |
| 38 | 0.048067 | 0.664202 | 3.071933 | 5.671261 | 3.544538 | 12.951933 |
| 39 | 0.034334 | 0.535606 | 2.775414 | 5.705018 | 3.949628 | 12.965666 |
| 40 | 0.023770 | 0.422569 | 2.472029 | 5.693157 | 4.388475 | 12.976230 |
| 41 | 0.015846 | 0.324850 | 2.165666 | 5.630732 | 4.862905 | 12.984154 |
| 42 | 0.010084 | 0.242017 | 1.860504 | 5.512605 | 5.374790 | 12.989916 |
| 43 | 0.006050 | 0.173445 | 1.561008 | 5.333445 | 5.926050 | 12.993950 |
| 44 | 0.003361 | 0.118319 | 1.271933 | 5.087731 | 6.518655 | 12.996639 |
| 45 | 0.001681 | 0.075630 | 0.998319 | 4.769748 | 7.154622 | 12.998319 |
| 46 | 0.000720 | 0.044178 | 0.745498 | 4.373589 | 7.836014 | 12.999280 |
| 47 | 0.000240 | 0.022569 | 0.519088 | 3.893157 | 8.564946 | 12.999760 |
| 48 | 0.000048 | 0.009220 | 0.324994 | 3.322161 | 9.343577 | 12.999952 |
| 49 | 0.000000 | 0.002353 | 0.169412 | 2.654118 | 10.174118 | 13.000000 |
| 50 | 0.000000 | 0.000000 | 0.058824 | 1.882353 | 11.058824 | 13.000000 |
| 51 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 12.000000 | 13.000000 |
| 52 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 13.000000 | 13.000000 |
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
ある人が私にこんな賭けを挑んできました。標準的なポーカーデッキから3つの数字を選び、予想を書きますが、最後まで伏せておきます。例えば、7-エース-2。すると彼は、もし3つ当てられたら、少なくとも1つの数字を当てられると賭け金を同額にすると申し出てきました。私の勝率はどれくらいでしょうか?
勝つには、相手が3つの予想をすべて間違える必要があります。最初の予想が間違っている確率は10/13です。2番目の予想が間違っている確率は9/12です。これは、最初のランクを可能性として推測した可能性を除外できるためです。3番目の予想が間違っている確率は8/11です。これは、最初の2つのランクを可能性として推測した可能性を除外できるためです。
勝つには、これら3つの条件がすべて満たされる必要があります。したがって、勝つ確率は(10/13) * (9/12) * (8/11) = 720/1716 = 41.96%となります。
均等な金額の場合、この賭けのあなたの側のハウスエッジは 16.08% です (痛い!)。
この質問は、Owen E'Shea 著の The Book of Proposition Bets (番号 7) から抜粋されました。
ある人が私に賭けを挑んできました。彼が27回振って、2つのサイコロの合計が12になるかどうかです。もし彼が12が出なければ、私は同額の賞金を獲得します。12が出る確率は1/36なので、彼が12を出すには平均36回振る必要があるのではないでしょうか?もし相手が27回しか出なかったら、私の方が有利になるように見えます。私の計算は正しいでしょうか?それとも私の計算のどこかに間違いがあるのでしょうか?
12が出るまでの平均的な待ち時間は、12が出るまでの時間を含めて36回です。しかし、これは36回投げるたびに12が出るという意味ではありません。12が出ない確率は(35/36)です。27回投げて12が出ない確率は(35/36)の27乗です。つまり、少なくとも1回12が出る確率は1-(35/36)の27乗=53.26%です。
以下の表は、20回から36回ロールした際に、少なくとも12が出る確率を示しています。ただし、イーブンマネーで有利になるには25回必要であることに注意してください。
確率12
| ロール | 確率 |
|---|---|
| 20 | 43.07% |
| 21 | 44.66% |
| 22 | 46.19% |
| 23 | 47.69% |
| 24 | 49.14% |
| 25 | 50.55% |
| 26 | 51.93% |
| 27 | 53.26% |
| 28 | 54.56% |
| 29 | 55.82% |
| 30 | 57.05% |
| 31 | 58.24% |
| 32 | 59.40% |
| 33 | 60.53% |
| 34 | 61.63% |
| 35 | 62.69% |
| 36 | 63.73% |
52 枚のカードの組み合わせは combin(52,5) = 2,598,960 通りあることが分かっています。私の質問は、5 デッキのシューから 5 枚のカードで何通りのハンドが考えられますか?
一度に 1 つのタイプの手を取り上げてみましょう。
- 同じカードが 5 枚: デッキには 52 種類のカードがあり、52 通りの組み合わせがあります。
- 同じカードが4枚:同じカードが4枚ある場合、その組み合わせは52通り、1枚しかない場合、51通りあります。つまり、フォー・オブ・ア・カインドの組み合わせは52×51=2,652通りあります。
- 同じカードが3枚と、別のカードが2枚の場合:同じカードが3枚の場合は52通り、ペアの場合は51通りあります。つまり、フルハウスの組み合わせは52×51=2,652通りあります。
- 同じカードが3枚と、異なるシングルトンが2枚の場合:同じカード3枚の組み合わせは52通り、シングルトン2枚の組み合わせはcombin(51,2)=1,275通りあります。つまり、スリーカードの組み合わせは52*1,275=66,300通りあります。
- 同じカードが2組ペアになり、シングルトンが1枚ある場合:ペアとなる2枚の異なるカードの組み合わせは、combin(52,2)=1,326通りあります。そして、シングルトンは50通り残ります。つまり、ツーペアとなる組み合わせは1,326*50=66,300通りあります。
- 同じカードが1組とシングルトンが3枚の場合:ペアのカードは52通りあります。残りのシングルトン51枚から3枚を選ぶ方法は、combin(51,3)=20,825通りあります。つまり、ペアの組み合わせは52*20,825=1,082,900通りです。
- 5 つのシングルトン: 52 枚の中から 5 枚のカードを選択する方法は combin(52,5)=2,598,960 通りあります。
これらの組み合わせの合計は 3,819,816 です。
この質問は、 Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。


