確率 - コイン
コインを 1000 回投げた場合、表が出る回数の合計が 452 ~ 548 の範囲になる確率はどれくらいでしょうか。
この問題では、二項分布の正規近似値を使用できます。表が出る回数の分散は1000*(1/2)*(1/2)=250です。したがって、標準偏差は250 1/2 =15.8114です。表が出る回数が548回未満の確率は、normdist((548+0.5-500)/15.8114) = 0.998920です。ここで、normsdistは、平均0、標準偏差1の正規分布に従う確率変数が、指定されたZスコアを下回る確率を求めるExcel関数です。次に、表が出る回数が452回未満の確率を引きます。これはnormdist((452-0.5-500)/15.8114) = 0.001080です。したがって、答えは0.99892-0.00108 = 0.997840です。繰り返しますが、これは近似値です。実際の答えは0.997856ですが、導出するのはより面倒です。平均すると、クラップスでポイントを獲得した後、プレイヤーはどのくらいの頻度でポイントを獲得するでしょうか?
ポイントが成立した確率は12回中5回で6または8、12回中4回で5または9、12回中3回で4または10となります。6または8が出る確率は11回中5回、5または9が出る確率は10回中4回、4または10が出る確率は9回中3回です。したがって、ポイントが成立したと仮定した場合、ポイントが成立する確率は、(5/12)*(5/11)+(4/12)*(4/10)+(3/12)*(3/9) = 40.61%となります。
魔法使いさん、50人がそれぞれ8回ずつコインを投げたら、8回連続で表か裏が出る人は50人のうち何パーセントくらいでしょうか?よろしくお願いします。
ある人が8回すべて表か裏が出る確率は、2×(1/2) 8 = 128分の1です。50人が平均して同じことをした場合、すべて表か裏が出るのは0.39人です。少なくとも1人がすべて表か裏が出る確率は32.44%です。
100枚のコインが入った袋があり、そのうち1枚は表裏のあるコインです。ランダムに1枚のコインを選び、10回連続で表が出るのを観察しました。表裏のあるコインを選んだ確率はどれくらいでしょうか?
これは教科書的なベイズ条件付き確率の問題です。一般的に、AがBを与えられた場合の確率は、AとBの確率をBの確率で割ったものです。この場合、Aは10回連続で表が出ており、Bは両面コインを選んでいます。AとBの確率は1/100です。これは、両面コインを選ぶ確率が100分の1であり、もし選んだ場合、10回連続で表が出る確率は100%だからです。ランダムに選んだコインを10回連続で投げた場合、10回連続で表が出る確率は(1/100)*1 + (99/100)*(1/2) 10 です。これは、両面コインを選ぶ確率が1%(10回連続で表が出る確率は100%)であるのに対し、表のコインを選ぶ確率は99%(10回連続で表が出る確率は(1/2) 10 )だからです。つまり、10回連続で表が出た場合、両面コインを選ぶ確率は0.01/(0.01*1 + 0.99* 0.000977) = 0.911843となります。
コインを投げて賭ける場合のアドバイスはありますか?
はい!私のアドバイスは、コインを投げ始めた時に表向きになっている面に賭けることです。Science News Onlineによると、コインが最初と同じ面に戻る確率は51%です。記事によると、その理由は、投げられたコインが軸の周りを完璧に回転せず、実際には回転していないのに回転しているように見えることがあるためです。この仮説は、コインが手のひらで捕まる場合にのみ当てはまり、コインが跳ね返ることは問題になりません。記事によると、回転するペニーコインは、重い表側が先に落ちるように重力で引っ張られるため、80%の確率で裏で落ちるとのことです。しかし、私はこの説に懐疑的です。私は20回試して、11回は表、9回は裏でした。20回のスピンで裏が9回以下で成功率が80%である確率は、1775分の1です。
回転するペニー硬貨の答えが見つかったかもしれません。10年以上前、小学6年生の時にペニー硬貨の回転に関する理科の課題をしました。オムニ誌で読んだのですが、ペニー硬貨を高速で回転させると、側面が表側に傾くため、ほとんどの場合、裏側が上に回転して止まるそうです。何百回も試してみましたが、ほとんど偏りのない結果が得られました。ただし、端に止まった2回だけは例外でした。
何時間も無駄にした後、ようやく回転速度が速すぎたことに気づきました。ゆっくり回すと、裏表が上に出るという、まさに理想の結果になりました。しかも、ペニーは完全に均一ではなく、一番細い部分から回し始めると、均一性が高まるようです。くだらないことだらけのチャートと、ペニーのように装飾された巨大なボール紙の円のおかげで、理科はAを取ったものの、宿題を全く無視したため、他の科目は全部落第しました。
そこで私は、10年以上前に行った、ほとんど何も覚えておらず、当時は自分が何をしていたのかよく分かっていなかった、ある粗雑な実験によって、あなたがおそらく少しばかり早口でペニーを回しすぎているだけかもしれないということを決定的に証明しました。
よし、もう一度ペニーをゆっくり100回回してみた。ゆっくりというのは、弾いてから結果が明らかになるまでの時間が2秒以上5秒未満という意味だ。ピカピカの2004-Dペニーを使った。結果は表が52回、裏が48回だった。つまり、どんな速度で回転するペニーでも、裏に大きく偏るという説には、まだ納得がいかない。
ある事象の「待ち時間」とは、その事象の確率の逆数だと私は理解しています。1つのサイコロを使って2が連続して出るまでの待ち時間を計算したいと考えています。シミュレーションでは平均42回出ます。この待ち時間を、2が連続して出る確率とどのように関連付ければよいでしょうか?
単一の事象において、確率がpであれば平均待ち時間は1/pであることは事実です。しかし、連続する事象の場合は状況はより複雑になります。xを、最後のロールが2でなかった状態とします。これは開始時の状態でもあります。yを、最後のロールが2だった状態とします。最初のロールの後、状態xに留まる確率は5/6、状態yに留まる確率は1/6です。Ex(x)を状態xからのロールの期待値、Ex(y)を状態yからのロールの期待値とします。すると…
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y)、そして
Ex(y) = 1 + (5/6)*ex(x)
これら 2 つの方程式を解くと...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x) = 7/6
例(x) = 36*(7/6) = 42
したがって、2 回連続して 2 が出る場合の平均待ち時間は 42 回です。
私も同じタイプの問題を抱えています。2 回表が出ると予想される回転数だけです。私の数学の問題のサイトで、問題 128 を参照してください。
ギャンブルゲームがあるとします。公平なコインを繰り返し投げます。1回投げるごとに1ルピーを支払う必要があります。結果はHかTの2通りです。表と裏の差が3になった場合、ギャンブラーから8ルピーを受け取ります。このゲームに参加すべきでしょうか?また、その理由は何でしょうか?勝つ確率はどれくらいでしょうか?7ルピーや9ルピーを受け取る場合、勝つ確率にどのような影響があるでしょうか?
開始点からの予想されるフリップ回数を x とします。
片側が多数派で 1 回投げた場合の残りの予想投げ回数を y とします。
片側が多数派で 2 回投げた場合の残りの予想回数を z とします。
E(x) = 1 + E(y)
E(y) = 1 + 0.5*E(x) + 0.5*E(z)
E(z) = 1 + 0.5*E(y)
すると、E(x) = 9、E(y) = 8、E(z) = 5 であることが簡単に分かります。つまり、表裏の差が3になるには平均9回投げる必要があります。つまり、8ルピーの場合、1回につき1ルピーを受け取る人にとっては良い賭けです。なぜなら、平均9ルピーを受け取りますが、支払うのは8ルピーだけだからです。ギャンブラーのハウスエッジは11.11%です。9ルピーなら妥当な賭けですが、7ルピーならハウスエッジは22.22%です。
何人かの方から、私の回答を詳しく説明してほしいと頼まれました。この解法には基本的な行列代数が必要です。
まず、x を答え、つまり表と裏の差が 3 になるまでの平均回数として定義します。
片側が 1 回転した時点から、期待される回転回数を y とします。
片側が 2 回めのフリップで上になっている時点からの期待されるフリップ回数を z とします。
最初のフリップの後、片側が1フリップで多数派になります。つまり、x=1+yです。
どちらかの側が1回ずつ先に進んでいる場合、もう1回投げると、最初の同点状態になるか、どちらかの側が2回ずつ先に進んでいるかのどちらかになります。どちらの結果も確率は同じです。つまり、y=1+0.5*x + 0.5*z
どちらかの側が2回先を行く場合、もう1回投げると、どちらかの側が1回先を行くか、ゲーム終了となります。繰り返しますが、どちらの結果も確率は同じです。つまり、z=1+0.5*y
したがって、3 つの方程式と 3 つの未知数があります。
(1)X=1+y
(2)Y = 1 + 0.5x + 0.5z
(3)Z = 1+0.5y
解くには、まず最後の 2 つの方程式に 2 を掛けて小数点を取り除きます。
(1)X=1+y
(2)2Y = 2+x + z
(3)2Z = 2+y
(1)の1+yを(2)のxに代入してみましょう。
2Y = 2 + 1 + y + z
(4) y = 3 + z
(3)においてyの代わりに3+zを代入することはできない。
2z = 2 + 3 + z
z = 5
ここで(4)のzを5に代入すると
(5)y = 3 + 5 = 8
(1)においてy = 8を代入すると、
(6)x = 9
友人が3回投げて表か裏が出る順番を選び、私に(別の)3回投げる順番を選ぶように指示しました。私たちは、どちらかの順番が出るまで、公平なコインを必要な回数投げます。友人がHHHを選んだ場合、私はどの順番を選ぶべきでしょうか?また、この賭けにおける私のアドバンテージはいくらでしょうか?友人が選んだ順番に基づいて、どの順番を選ぶべきかをどのように計算すればよいでしょうか?
次の表は、プレイヤー A とプレイヤー B が選択したすべての可能なパターンに応じて、プレイヤー A が勝つ確率を示しています。
プレイヤーAの勝利確率
| プレイヤーA | プレイヤーB | |||||||
| ああ | HHT | HTH | HTT | THH | THT | TTH | TTT | |
| ああ | 1/2 | 2/5 | 2/5 | 1/8 | 5月12日 | 3/10 | 1/2 | |
| HHT | 1/2 | 2/3 | 2/3 | 1/4 | 5/8 | 1/2 | 7/10 | |
| HTH | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/8 | 7月12日 | |
| HTT | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/4 | 7/8 | |
| THH | 7/8 | 3/4 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| THT | 7月12日 | 3/8 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| TTH | 7/10 | 1/2 | 5/8 | 1/4 | 2/3 | 2/3 | 1/2 | |
| TTT | 1/2 | 3/10 | 5月12日 | 1/8 | 2/5 | 2/5 | 1/2 | |
最適なパターンを選ぶための記憶装置として、相手の1番目と2番目の選択は、それぞれあなたの2番目と3番目と同じである必要があります。あなたの1番目の選択は、3番目の選択の反対である必要があります。例えば、相手がHTTを選択した場合、2番目と3番目の選択はHTである必要があります。あなたの最後の選択はTであるため、HHTパターンの場合は、1番目はHである必要があります。この戦略に従うと、相手がどのパターンを選択するかに応じて、勝率は2/3から7/8になります。
こんにちは、パティです。素敵なサイトをお持ちですね。とても知識豊富な方ですね。まさにカジノで隣にいてほしいタイプの男性です!!!!!!! 何かお力添えいただけないでしょうか?彼氏に、インターネットで問題の解決策を探すと言っていたんです。もし助けていただけたら、本当に助かります。
彼氏がコイン収集家で、小麦ペニー硬貨を袋ごと買ってきてくれたんです。私自身、コインについてはあまり詳しくないんです(彼が時間をかけて教えてくれるんです)。でも、ある特定の年のコインが袋に入っていないことに驚いたと言っていました。コインはよくあるものなのに、その確率は10億分の1しかないらしいんです。彼には、オフィスの人たち(自称天才たち!!)に聞いてみよう、もし分からなかったらネットで少し調べてみよう、と言いました。それで、あなたに出会ったんです。
とにかく、もし助けていただけるなら、本当に助かります。袋には約5,500枚のペニー硬貨が入っていました。アメリカの全造幣局で鋳造された小麦ペニー硬貨の総数は24,267,000,000枚です。1955年製(彼が探していたもの)のペニー硬貨は3億30,000,000枚でした。私のオフィスの何人かは、人口動態や、造幣局がすべてのペニー硬貨を配布しなかった可能性など、他の要因もあると言っています。…………彼らの言うことは正しいと思いますが、私(そしてきっと私のボーイフレンドも)は、おおよその確率を知ることにします!!!!!!!!! 助けていただければ幸いです。
あなたの鋳造数はマウンテンビュー・コインズのものとほぼ同じです。これまでに鋳造された小麦ペニー硬貨がすべて同じ確率で袋の中に入っていると仮定すると、どのペニー硬貨も55番ではない確率は(24,267,000,000-330,000,000)/24,267,000,000 = 0.986401286となります。5500枚の硬貨が55番ではない確率は、ほぼ近似値で、0.986401286 5500 = 507,033,772,284,213,000,000,000,000,000,000分の1となります。
父はコイン収集家なので、この件について助けを求めました。父はこう言いました。
私の推測ですが、1955年にフィラデルフィアで鋳造されたリンカーン・セント硬貨のうち、日付が2回刻印されたものが少数ありました。正確な数は誰も知りません。この誤りが発見される前に、流通のために他のセント硬貨と混ぜられていたのです。現在、流通していない標本は2000ドルから6000ドルほどの価値があります。この「ウィート」硬貨の袋から、2回刻印の標本を探している誰かによって、1955年のものは全て取り除かれてしまったのではないかと疑っています。ここに1枚の写真を載せます: 1955年 2回刻印 表面1セント硬貨。
このウェブサイトでは「ウィート」を販売しており、ディーラーがコインを回収した後、既に一部の日付の選別が行われていることは間違いありません。1955年発行のダブルダイではないものはコレクションに戻されていると考えていましたが、もしかしたら別々に売却されたり、溶かされたりしているのかもしれません。ウィート・ペニーの銅は、現在では1セントよりもはるかに価値があります。だからこそ、数十年前に銅メッキの亜鉛セントに切り替えられたのです。造幣局自身が1955年発行のコインを多く流通させないことに決め、希少なダブルダイの標本を求めての慌ただしい争奪戦を避けるために、鋳造後に溶かされた可能性があります。造幣局と郵便局は印刷ミスを常に恥じており、流通させないように努めています。
5500枚のコインをプレイしていく中で、除去の影響を考慮すると「近似値」と推測します。除去の影響は微々たるものですね!これは、非対象コインを除去するにつれて、対象コインが出現する可能性が低くなるという良い例です。なぜなら、除去の影響は、不正なゲーム、つまり対象コインが除去されるという、はるかに大きな確率に比べて非常に小さいからです。
はい、「ほぼ近い」と言いました。なぜなら、世の中には1セント硬貨の数が限られているからです。袋から55セント硬貨以外の1セント硬貨を1枚取り除くと、その影響で袋の中の残りの1セント硬貨がすべて55セント硬貨である確率が高まります。もし「ほぼ近い」と言わなかったら、少なくとも3人は訂正のメールを送ってくれたでしょう。もちろん、これは極めて微々たる効果ですが、私の読者の多くは完璧主義者で、ほんのわずかな間違いでも私を責め立てるでしょう。
部屋に2つのテーブルがあります。右側のテーブルには100枚のコインがあり、そのうち20枚はH面を上に、残りの80枚はT面を上にしています。もう一方のテーブルにはコインはありません。目標は、両方のテーブルでH面を上にしたコインの数が等しくなるように、コインをどうにかして動かすことです。コインは見えません(部屋は暗いため)。また、触って「上」か「下」か確認することもできません。
解答については、私の別のサイト mathproblems.info をご覧ください (ネタバレ注意!)
友人が、コインを100回投げて、表と裏がちょうど50回出るかどうかに3対1のオッズで20ドル賭けてくれないかと提案してきました。もしそうなれば60ドルの勝ち、そうでなかったら20ドルの借金を背負うことになります。賭けるべきだったでしょうか?また、50/50が最も起こりやすい結果ではないとしたら、もっと起こりやすい結果(例えば51/49)はあるのでしょうか?
それぞれちょうど50枚出る確率は、( 100,50)*(1/2) 100 = 7.96%です。公平なオッズは11.56対1です。つまり、3対1ではハウスエッジが68.2%という、ひどい賭けです。これはあなたの友達のおかげですね。表と裏が50/50になる確率が最も高い賭けです。興味深い賭けは、表と裏の数が47から53の間に入るかどうかです。その範囲内に入る確率は51.59%です。もし合計がその範囲外になることに賭けてくれる人が見つかったら、イーブンマネーで3.18%のアドバンテージが得られます。
次の表は、30 ~ 70 回の表/裏のそれぞれの確率を示しています。
100回投げた場合の表/裏の合計の確率
| 表/裏 | 確率 |
|---|---|
| 30、70 | 0.000023 |
| 31、69 | 0.000052 |
| 32、68 | 0.000113 |
| 33、67 | 0.000232 |
| 34、66 | 0.000458 |
| 35、65 | 0.000864 |
| 36、64 | 0.001560 |
| 37、63 | 0.002698 |
| 38、62 | 0.004473 |
| 39、61 | 0.007111 |
| 40、60 | 0.010844 |
| 41、59 | 0.015869 |
| 42、58 | 0.022292 |
| 43、57 | 0.030069 |
| 44、56 | 0.038953 |
| 45、55 | 0.048474 |
| 46、54 | 0.057958 |
| 47、53 | 0.066590 |
| 48、52 | 0.073527 |
| 49、51 | 0.078029 |
| 50 | 0.079589 |
n 回の試行のうち w 回が勝つ確率 (各勝利の確率は p) の一般的な式は、combin(n,w) × p w × (1-p) (nw) = [n!/(w! × (nw)!] × p w × (1-p) (nw)です。
コインを 1,000 回投げた場合、少なくとも 10 回連続して表または裏が出る可能性はどれくらいでしょうか。
面白い質問ですね。ちょうど別の読者からこのテーマに関する学術論文が送られてきたんです。その論文には以下のグラフが掲載されていて、確率は約62%と示されています。
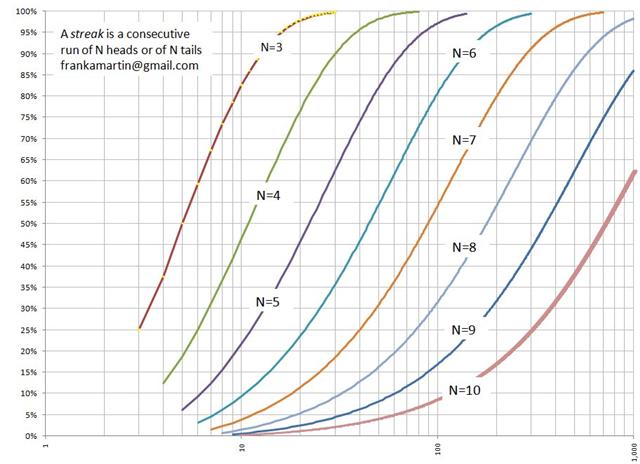
このトピックの詳細については、Frank Martin 著の「カジノでこのようなひどい連敗を喫する確率はどれくらいだったのか?」 (483K) をご覧ください。
コインを 100 回投げた場合、少なくとも 1 回は 7 回連続で表が出る可能性はどれくらいでしょうか。
簡単な非再帰的な式で答えられるかどうかは分かりませんが、簡単な再帰的な式はあります。
f(n)= pr(最初の投げで表が出る)×f(n-1) +
pr(1回目の投げで表、2回目の投げで裏)×f(n-2) +
pr(最初の2回で表、3回目で裏)×f(n-3) +
pr(最初の3回で表、3回目で裏)×f(n-4) +
pr(最初の4回で表、4回目で裏)×f(n-5) +
pr(最初の5回で表、5回目で裏)×f(n-6) +
pr(最初の6回で表、6回目で裏)×f(n-7) +
pr(最初の7回の表) =
(1/2)×f(n-1) +
(1/2) 2 ×f(n-2) +
(1/2) 3 ×f(n-3) +
(1/2) 4 ×f(n-4) +
(1/2) 5 ×f(n-5) +
(1/2) 6 ×f(n-6) +
(1/2) 7 ×f(n-7) +
(1/2) 7
どこ:
f(n) = n回のフリップ内で成功する確率。
pr(x) = xが起こる確率。
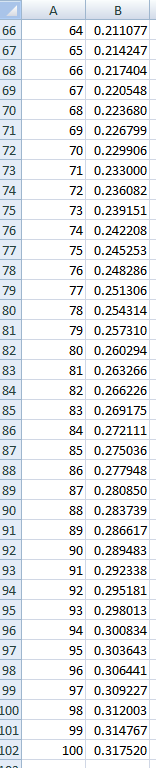
スプレッドシートはこのような問題に最適です。下のスプレッドシートのスクリーンショットでは、セルB2からB8に確率0を設定しています。これは、6回以下の投げ方で7回連続で表が出ることはないためです。セルB9には、次の数式を入力しました。
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
次に、セルB10からセルB102にコピー&ペーストしました。これは100回の投げに相当します。その確率は0.317520です。ランダムシミュレーションで確認しました。
 |  |
この記事が最初に公開された後、リック・パーシー氏が行列代数の解法を私と共有してくれました。以下に私の言葉で解説します。読者は既に行列代数の基礎をご存知であると想定しています。
まず、フリッパーがどの時点でも取り得る状態は 8 つあります。
p 1 = 現在の時点からさらに 7 回表が出た場合の成功確率。
p 2 = 現在の時点からさらに 6 回表が出た場合の成功確率。
p 3 = 現在の時点からさらに 5 回表が出た場合の成功確率。
p 4 = 現在の時点からさらに 4 回表が出た場合の成功確率。
p 5 = 現在の時点からさらに 3 回表が出た場合の成功確率。
p 6 = 現在の時点からさらに 2 回表が必要な場合の成功確率。
p 7 = 現在のポイントからさらに 1 回表が必要な場合の成功確率。
p 8 = それ以上表が必要ない場合の成功確率 = 1。
最大行列S n を、n回目の投げの後に各状態になる確率として定義しましょう。S 0 は最初の投げの前の確率を表し、状態0になる確率は100%です。つまり、S 0 =
| 1 0 0 0 0 0 0 0 |
Tを2つの連続する反転、つまりS nからS n+1への変換行列とする。ここでS n+1 = T × S n
- 状態 1 の場合、1 回の投げ後に状態 2 (表) になる確率は 0.5、状態 1 (裏) のままになる確率は 0.5 です。
- 状態 2 の場合、1 回投げると状態 3 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 3 の場合、1 回投げると状態 4 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 4 の場合、1 回の投げ後に状態 5 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 5 にいる場合、1 回投げた後、状態 6 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 6 の場合、1 回の投げ後に状態 7 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 7 の場合、1 回の投げ後に状態 8 (表) になる確率は 0.5、状態 1 (裏) に戻る確率は 0.5 です。
- 状態 8 の場合、成功を達成しており、確率 1.0 で状態 8 のままになります。
これらを遷移行列Tの形で表すと、
| 0.5 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.5 0.0 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.5 0.0 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.5 0.0 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.5 0.0 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.5 0.0 |
| 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
1 回のめくり後の各状態の確率を取得するには...
(1) S1 = S0 ×T
2回めくってからはどうでしょうか?
(2) S2 = S1 ×T
式(1)を式(2)に代入してみましょう。
(3) S 2 = S 0 × T × T = S 0 × T 2
3回めくった後はどうですか?
(4) S 3 = S 2 × T
式(3)を式(4)に代入すると…
(5) S 3 = S 0 × T 2 × T = S 0 × T 3
100 回目のフリップ後、州までこれを続けることができます...
S 100 = S 0 × T 100
では、T 100とは何でしょうか?コンピュータが登場する前は、このような計算は大変な苦労だったに違いありません。しかし、ExcelのMMULT関数とコピー&ペーストを駆使すれば、T 100 = という式が得られます。
| 0.342616 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.317520 |
| 0.339863 0.170617 0.085653 0.042999 0.021586 0.010837 0.005440 0.323005 |
| 0.334379 0.167864 0.084271 0.042305 0.021238 0.010662 0.005352 0.333929 |
| 0.323454 0.162380 0.081517 0.040923 0.020544 0.010313 0.005178 0.355690 |
| 0.301693 0.151455 0.076033 0.038170 0.019162 0.009620 0.004829 0.399038 |
| 0.258346 0.129694 0.065109 0.032686 0.016409 0.008237 0.004135 0.485384 |
| 0.171999 0.086347 0.043347 0.021761 0.010924 0.005484 0.002753 0.657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
右上の項は、100 回のフリップ後に状態 8 になる確率を示しており、0.317520 です。
オーストラリアのクリケット選手が、コイントスの判定を35試合連続で間違え、36試合目で正解したという話を聞いたことがありますか?そんな確率はどれくらいでしょうか?
あなたがおっしゃるまで、その話は知りませんでした。おっしゃっているのは、マグパイズの10代のクリケット選手、クリスティ・ペリンさんの驚くべき話です。彼女はコイントスを35回連続で間違えたのです。35回以上間違える確率は、(1/2) 35 = 34,359,738,368分の1です。ちなみに、パワーボールに当たる確率は195,249,054分の1です。これは、35回連続でコイントスを外す確率の176倍です。
コインを投げて賭ける場合のアドバイスはありますか?
はい!投げる人の手の中の表向きの面に賭けましょう。ペルシ・ディアコニス、スーザン・ホームズ、リチャード・モンゴメリーによる学術論文「コイントスにおける動的バイアス」では、コインが投げた面と同じ面に落ちる確率は51%と結論付けられています。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
50/50のゲームで2回連続で負けるには、平均して何回試行する必要がありますか?3回連続、4回連続、n回連続で負ける場合はどうでしょうか?
まず、2 人が負けた場合を解決してみましょう。
x を、最初から、または勝利した後に予想される将来のコイントスの回数とします。
1 回の負けの後の将来の予想フリップ回数を y とします。
次の 2 つの方程式を立てることができます。
(1)x = 1 + 0.5x + 0.5y
1は、プレイヤーが状態を変えるためにコインを投げなければならないことを表しています。勝てば状態xのままになる確率は50%です。負ければ状態yに進む確率は50%です。
(2)y = 1 + 0.5x
再び状態yから、1はその時点でのコイントスを表します。勝利の確率は50%で、状態xに戻ります。敗北の確率は50%で、ゲームは終了し、追加のコイントスは不要になります。つまり、0.5*0となります。
両方の式を 2 倍にして並べ替えると次のようになります。
(3)x - y =2
(4)-x + 2y = 2
2 つの方程式を追加すると次のようになります。
(5)y = 4
これを(1)から(4)までの任意の方程式に代入するとx=6になります。
3 つの損失の場合、3 つの可能な状態を次のように定義します。
x を、最初から、または勝利した後に予想される将来のコイントスの回数とします。
1 回の負けの後の将来の予想フリップ回数を y とします。
2 回負けた後の将来のフリップの予想回数を z とします。
初期方程式は次のとおりです。
x = 1 + 0.5x + 0.5y
y = 1 + 0.5x + 0.5z
z = 1 + .5x
初期状態を行列形式で次のように設定できます。
| 0.5 | -0.5 | 0 | 1 |
| -0.5 | 1 | -0.5 | 1 |
| -0.5 | 0 | 1 | 1 |
行列代数を覚えていれば、xを行列式(A)/行列式(B)として解くことができます。
A =
| 1 | -0.5 | 0 |
| 1 | 1 | -0.5 |
| 1 | 0 | 1 |
B =
| 0.5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
| 0.5 | -0.5 | 0 |
| -0.5 | 1 | -0.5 |
| -0.5 | 0 | 1 |
Excelには便利な行列式関数「=mdeterm(範囲)」があります。この場合、x = mdeterm(行列A)/mdeterm(行列B) = 1.75/0.125 = 14となります。
連続して負けた場合も再帰処理を使うことができます。4を考えてみましょう。上記の例から、3連敗するには平均14回投げる必要があることがわかります。その時点でコインはもう一度投げられ、50%の確率で最初からやり直しになります。つまり、
x = 14 + 1 + x/2
x/2 = 15
x = 30
つまり、前の答えに 1 を加えて、それを 2 倍にします。
このパターンは簡単に見分けられます。n回連続で負ける場合の期待値は2 n+1 -2です。
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されました。
公平なコインを n 回投げた場合、少なくとも 1 回は t 面の裏が出る可能性はどれくらいでしょうか。
答えは 1-F (t) n+2 /2 nです。ここで、 F (t) n はt ステップのフィボナッチ数列の n 番目の数です。
フィボナッチ数列とは何か、と疑問に思うかもしれません。最初の数は1です。tステップ数列では、後続の数は前のt個の数の和になります。最初の数より前の数はすべて0であると仮定します。
2段階の数列を見てみましょう。最初の数は1です。2番目の数は前の2つの数の和です。1の前に0があると仮定すると、2番目の数は0+1=1です。3番目の数は1+1=2、4番目の数は1+2=3、5番目の数は2+3=5です。
最初の 12 個の 2 ステップ フィボナッチ数は、1、1、2、3、5、8、13、21、34、55、89、144 です。
例を見てみましょう。10回投げて少なくとも1回は2回連続して裏が出る確率はどれくらいでしょうか?
必要なのは2つの裏表だけなので、2段階のフィボナッチ数列を使います。数列の12番目の数(裏表の回数より2多い数)は144です。したがって、答えは1-F (2) 10+2 /2 10 = 1 - 144/2 10 = 1 - 144/1024 = 85.94%です。
20 回投げて 5 回連続して裏が出る可能性はどのくらいでしょうか?
最初の 22 個の 5 ステップ フィボナッチ数は、1、1、2、4、8、16、31、61、120、236、464、912、1793、3525、6930、13624、26784、52656、103519、203513、400096、786568 です。
答えは1 - F (5) 20+2 /2 20 = 1 - 786,568/1,048,576 = 1 - 75.01% = 24.99%となります。
この質問はWizard of Vegasの私のフォーラムで議論されています。
表が出る確率が60%の偏ったコインがあります。このコインを、2回連続で表か裏が出るまで投げます。最初に2回連続で表が出る確率はどれくらいでしょうか?
魔法使いよ、賭けを挑む。ルールはこうだ。
- 表(H)と裏(T)のパターンはお好きなものをお選びください。例:HTT。
- あなたのパターンを明らかにした後、私は私のものを選択します。
- 一つのパターンが順番に現れるまで、コインを何度も投げます。そのパターンを選んだ人が勝ちです。
- 私は3対2のオッズを与えます。
よろしいでしょうか?ご希望に応じて何度でもお引き受けします。
いいえ。いい試みですね。後攻のプレイヤーは大きなポジションアドバンテージを持っています。後攻のプレイヤーの戦略と勝率は次のとおりです。
オディウスギャンビットゲーム戦略
| プレイヤー1 | プレイヤー2 | Pr. プレイヤー2の勝利 |
|---|---|---|
| ああ | THH | 87.50% |
| HHT | THH | 75.00% |
| HTH | HHT | 66.67% |
| HHT | THH | 75.00% |
| THH | HTT | 75.00% |
| THT | TTH | 66.67% |
| TTH | HTT | 75.00% |
| TTT | HTT | 87.50% |
上の表が示すように、私が勝つ可能性が最も高い、あるいはあなたが勝つ可能性が最も低いのは、私が THT または HTH を選択した場合ですが、その場合でも私の勝率は 3 分の 1 にすぎません。公平な賭けであるためには 2 対 1 になるはずなので、3 対 2 になったとしても、あなたの優位性は 16.67% になります。
プレイヤー2の戦略を覚える方法を紹介します。P(x)をプレイヤー1のポジションxの選択とします。O(x)をプレイヤー1のポジションxの選択の反対とします。プレイヤー2は常にO(2) - P(1) - P(2)を選択します。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
公平なコインを40回投げた場合、表が5回連続し、裏が5回連続する確率はどれくらいでしょうか?「1回連続」とは少なくとも1回、「5回連続」とは少なくとも5回連続することを意味します。表と裏の連続は必ずしも隣接している必要はありません。
回答は以下のボタンをクリックしてください。
これが私の解決策です(PDF)。
この質問は 、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
ヘンリーとトムはコインを投げて賭けることにしました。表が出ればヘンリーが勝ち、裏が出ればトムが勝ちます。
1回1ドルの賭け金で、彼らは本当に退屈だったので、100万回投げることにしました。セッションの最後に、負けた人は勝者に最終的な残高を小切手で支払います。小切手の期待値はいくらでしょうか?
[スポイラー=答え] 797.88456080286535587989211986876373695171726 232986931533185165934131585179860367700250466 781461387286060511772527036537102198390911167 448599242546125101541269054116544099863512903 269161506119450728546416733918695654340599837 28381269120656178667772134093073... [/spoiler]
答えの一般的な式は sqrt(variance * (2/pi)) です。
この場合の分散は1,000,000です。したがって、実際の結果と期待される結果の絶対差の期待値は、sqrt(1,000,000 × (2/π)) =~ 797.88456080286535587989211986876373695171726 232986931533185165934131585179860367700250466 781461387286060511772527036537102198390911167 448599242546125101541269054116544099863512903となります。 269161506119450728546416733918695654340599837 28381269120656178667772134093073。
Ask the Wizard #358で関連する質問をします。これは、sqrt(2/pi) の項がどこから来たのかを示すのに役立ちます。
この質問はWizard of Vegas のフォーラムで尋ねられ、議論されました。
カジノで、公平なコイン投げで配当が均等になるゲームがあるとします。プレイヤーは1回1ドルの賭け金で100万回プレイしたいと考えています。破産しない確率を50%にするには、いくらの金額をテーブルに持ち込むべきでしょうか?
まず、プレイヤーの資金が無制限であると仮定して、100 万回のフリップ後にプレイヤーが x ユニット以上負ける確率はどれくらいかという質問に答えましょう。
これは公平な賭けなので、100万回投げた後の平均勝率は0です。各投げの分散は1なので、100万回投げた場合の分散は100万です。したがって、1標準偏差はsqrt(1,000,000) = 1000です。
必要なバンクロールは、Excel関数 =norm.inv(確率,平均,標準偏差) で計算できます。例えば、=norm.inv(.25,0,1000) と入力すると、-674.49 という結果になります。これは、100万回投げた後、プレイヤーが674以上の負けになる確率が25%あることを意味します。これはあくまで推定値であることにご注意ください。真の答えを得るには二項分布を使用する必要がありますが、100万回投げるとなると非常に面倒な計算になります。
プレイヤーが674ドルをテーブルに持っていった場合、100万ドルを投げる前に資金が尽きてしまう可能性は十分にあります。もしクレジットでプレイを続けることができれば、損失を取り戻し、674ドル未満の損失で終えられるかもしれません。実際、プレイヤーが-674になった後、将来のある時点で-674を上回るか下回るかは50/50の確率です。
したがって、プレイヤーがクレジットでプレイできる場合、結果は 3 つ考えられます。
- プレイヤーは -674 を下回ることはありません。
- プレーヤーはある時点で -674 を下回りますが、回復して -674 を超えて終了します。
- プレイヤーはある時点で -674 を下回り、プレイを続けてさらに損失を被ります。
シナリオ 3 の確率は 25% であることがわかりました。
シナリオ 2 はシナリオ 3 と同じ確率であるはずです。なぜなら、プレイヤーが -674 負けると、100 万回投げた後にそのポイントを上回るか下回るかの確率が 50/50 になるからです。
シナリオ 1 は唯一の他の選択肢であり、その確率は 100%-25%-25% = 50% である必要があります。
プレイヤーが 674 を下回らない確率が 50% の場合、下回る可能性は 100% - 50% = 50% になります。
つまり、元の質問に対する答えは 674 ドルです。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。


