確率 - パズル
サイコロを振る確率について具体的な情報を知りたいと思っています。6個のサイコロを一度に振った場合、すべて1が出る確率は46,656分の1です。1個から5個まで1が出る確率はどれくらいでしょうか。このような問題を計算するのに使うべき公式を知りたいです。
y個のサイコロのうちx個が1になる確率は、combin(y,x)*(1/6) x *(5/6) yxです。combin(x,y)関数の説明については、ポーカーにおける確率のセクションを参照してください。例えば、4個の1が出る確率は、combin(6,4)*(1/6) 4 *(5/6) 2 = 0.803755%です。
6つのサイコロの1の数
| 1つ | 確率 |
|---|---|
| 0 | 0.3348980 |
| 1 | 0.4018776 |
| 2 | 0.2009388 |
| 3 | 0.0535837 |
| 4 | 0.0080376 |
| 5 | 0.0006430 |
| 6 | 0.0000214 |
| 合計 | 1.0000000 |
8人のゴルファーが新しいコースへ行きました。キャディーマスターは4台のカートに8つのバッグをランダムに積み込みました。ゴルファーたちは帽子の中に8つのマーク付きゴルフボールを入れました。ボールは空中に投げられました。互いに近い2つのボールはパートナーです。いずれの場合も、パートナーのゴルフバッグは既に同じカートに積まれていました。投げる前にゴルフバッグが正しくペアになっている確率はどれくらいでしょうか?
組み合わせの数を求める公式は、combin(8,2)*combin(6,2)*combin(4,2)/fact(4) = 25*15*6/24 = 105 となります。組み合わせの数を求める別の方法は、ゴルファーをランダムに1人選びます。彼とペアになる可能性のある人は7人います。次に、残りの6人から別のゴルファーをランダムに選びます。彼とペアになる可能性のある人は5人います。次に、残りの4人から別のゴルファーをランダムに選びます。彼とペアになる可能性のある人は3人います。したがって、組み合わせの数は7*5*3 = 105 となり、答えは105分の1となります。
友人がこれを送ってくれたのですが、これがどのように機能するかについての公式があるかどうか知りたいです。
こうした心理読解パズルがうまくいくのは、しばしば興味深い数学的奇癖によるものです。ある数の桁の合計が9で割り切れる場合、その数自体も9で割り切れます。ラスベガス・トロピカーナの電話番号(702-739-2222)で試してみましょう。桁の合計は7+0+2+7+3+9+2+2+2+2 = 36です。36は9で割り切れるので、702739222も9で割り切れるはずです。これがその証明です。
- n を任意の整数とします。n を d 0 *1 + d 1 *10 + d 2 *100+ d 3 *1000+ ... + d n *10 nと表します。ここで、d nは最初の数字、d n-1は2番目の数字、というように続きます。
- n = [d 0 + d 1 + d 2 + ... + d n ] + [d 1 *9 + d 2 *99+ d 3 *999+ ...+ d n *999...9 (9がn個ある数)]
- n = [d 0 + d 1 + d 2 + ... + d n ] + 9*[d 1 *1 + d 2 *11+ d 3 *111+ ... d n *111...1 (n個の1を持つ数)]
- 9*任意の整数は9で割り切れます。したがって、d 0 + d 2 + d 2 + ... + d n 、つまり数字の合計が9で割り切れる場合、その数全体も9で割り切れる必要があります。
証明が終わったので、今度はこのマジックトリックを見てみましょう。問題は、任意の数字を選び、その数字を並べ替えて2つ目の数字を作ることです。そして、大きい数から小さい数を引きます。
答えは常に9で割り切れる数字の合計になります。なぜでしょうか?元の数の各桁は、別の数のどこかに現れるからです。一度に1組の数字を取り出し、他のすべての数字を0に置き換えると、各組は+/- n*[10 x - 10 y ](x>=y、nは数字)= +/-n *10 y *(10 xy - 1)= 10 y *(9だけで構成される数)= 9で割り切れる数となります。
例を見てみましょう。元の数字が1965だとします。これを混ぜ合わせると6951になります。6951 - 1965 = 6*(1000-10) + 9*(100-100) + 5*(10-1) + 1*(1-1000) = 6*990 + 9*0 + 5*9 + 6*-999。それぞれの数字は9で割り切れるので、引き算した数字も9で割り切れ、最終的に各桁の合計も9で割り切れることに注意してください。
次に、0以外の数字を丸で囲み、残りの数字の合計を入力するように指示されます。プログラムは、入力した数字に9で割り切れる数字を足すだけで済みます。例えば、数字の合計が13だった場合、5を丸で囲む必要があります。13+5 = 9で割り切れる数字だからです。
ゼロを丸で囲むことができない理由は、ゼロを丸で囲んだ後に、すでに 9 で割り切れる数字を入力した場合、プログラムが 0 を丸で囲んだのか、9 を丸で囲んだのかを認識できないためです。
素晴らしいサイトですね。確率と統計に興味を持つギャンブラーとして、よくこのサイトを参照しているのですが、実はこの質問は私の仕事に関係しています。人事部から、少人数のスタッフ(5人)をベルカーブ(ベルカーブ)で評価するように言われています。つまり、全従業員の上位5%に1人、次の20%に1人、次の50%に1人、次の20%に1人、そして下位5%に1人というように評価するのです。この会社の従業員数は約5000人です。これほど少ないサンプル数でこの分布に当てはまる確率はどれくらいでしょうか?
お褒めいただきありがとうございます。これは良い問題です。従業員のうち1人が下位5%に入る確率は、5*(.05)*(.95) ≒ 0.203627です。従業員のうち1人が下位5%に入る場合、次の20%に入る確率は、4*(.2/.95)*(.75/.95) ≒ 0.414361です。この2人の成績不振者を考えると、残りの75%のうち次の50%に入る確率は、3*(.5/.75)*(.25/.75 ) ≒ 0.222222です。残りの2人のうち1人が下位25%に入る確率は、2*(.2/.25)*(.05/.25) = 0.32です。これらすべての確率を積算すると、0.006、つまり 1% の 3/5 になります。
順序統計量(列番号100 )について質問された方へ、2つの不満点があります。1つは小さな点、もう1つは大きな点です。あなたの方法では有限母集団補正ができませんでした。従業員が5000人であれば、これは簡単なことかもしれませんが、従業員が20人だったら絶対にできなかったでしょう!
しかし、もっと重要なのは、あなたは暗黙のうちに、管理者が従業員に影響を与えないと仮定していることです。優秀な管理者が、賢明な採用と解雇、あるいは平均以上の動機付けスキルによって、従業員の平均レベルを向上させたとしましょう。この影響を考慮に入れなければ、結果として得られる確率は上方または下方にバイアスがかかります。あなたはご存知でしょうが、私は差別訴訟でこのような計算を数多く行っており、調整可能な要素(この場合は集団固有の影響)を調整しないと、しばしば人々を誤った方向に導く可能性があるため、この点には敏感です。
良い点を指摘していただき、ありがとうございます。しかし、職務遂行評価の配分をコントロールできないことの代償は、評価のインフレです。管理職は、部下の満足度を維持するために、過大な評価を下さざるを得なくなります。10年間公務員として勤務してきた経験から、この点についてはある程度の経験があります。UNLVで教えていた頃は、クラス平均GPAの基準はありませんでしたが、学期末の成績評価曲線がどうなっているべきかについては、ある程度の期待値がありました。少なくとも大学という環境においては、それは妥当な方針だと思いました。ビジネス環境においては、何らかの常識的な基準を設けるのが最善かもしれません。
ゲーミング数学者が直面している有名な未解決問題は何かありますか?例えば、ギャンブルの世界におけるフェルマーの最終定理など。もしあれば、例を挙げていただけますか?
いい質問ですね。思いつきません。
これはどのように機能しますか: www.1800gotjunk.com/genie/ ?
10t+u と表してみましょう。各桁の数字を引き算すると、10t+utu = 9t となり、9 で割り切れる数になります。9 で割り切れる数はすべて同じ数字を持つことに注目してください。それが精霊が予言する数字です。
私は専門資格試験を受けようとしています。規則では次のように定められています。
- 試験は7科目から構成されます。
- 各科目ごとに60問の多肢選択式問題が出題されます。
- 各多肢選択問題には 4 つの回答が可能ですが、正解は 1 つだけです。
- 合格するには、受験者は少なくとも 75% の平均点を取得し、どの科目でも 65% 未満の成績を取ってはなりません。
私の質問は、受験者がすべての答えを推測した場合、試験に合格する可能性はどれくらいでしょうか?言い換えれば、運だけで試験に合格する確率はどれくらいでしょうか?
75%の要件を満たすには、420問中少なくとも315問正解する必要があります。推測による正答数の期待値は420*0.25=105です。標準偏差は(420*0.25*0.75)^0.5=8.87412です。つまり、受験者は期待値を210問、つまり210/8.87412=23.66432標準偏差上回る必要があります。この確率は桁外れです。地球上のすべての生物がこのテストを受け、無作為に答えたとしても、誰も、あるいは何も合格できないでしょう。もう一つの要件については触れません。
ある大学のフットボール チームが第 1 試合に勝つ確率が 10%、第 2 試合に勝つ確率が 30%、両方の試合に負ける確率が 65% の場合、正確に 1 回勝つ確率はどれくらいでしょうか。
両試合が独立していると仮定した場合、両試合に負ける確率は90%×70%=63%となります。しかし、両試合に負ける確率は実際には65%(63%よりも高い)だとおっしゃっているので、両試合は相関関係にあることになります。両試合に負ける確率が65%で、第2試合に負ける確率が70%だとすると、第1試合に勝ち、第2試合に負ける確率は5%になります。同じ論理で、第1試合に負け、第2試合に勝つ確率は25%になります。つまり、両試合に勝つ確率は5%しか残らないということです。つまり、両試合に勝つ確率は25%+5%=30%となります。
ゲーム番組Let’s Make a Deal には、3つのドアがあります。例として、2つのドアが山羊を表しており、1つのドアが新しい車を表しているとします。ホストのモンティ・ホールはドアを選ぶために2人の出場者を選びます。モンティが最初にドアを開けるたびにヤギが現れます。今回は最初の出場者のものだったとしましょう。モンティが実際にこれを行ったことはありませんが、モンティが他の競技者にこの時点でドアを他の未開封のドアに切り替える機会を提供した場合はどうなりますか。彼は切り替える必要があるのでしょうか?
はい! この問題の鍵は、ホストがヤギでドアを開ける運命にあるということです。 彼はどのドアに車があるかを知っているので、プレイヤーがどのドアを選んでも、最初にヤギを明らかにすることができます。 この問題は「モンティ・ホールのパラドックス」として知られています。 それについての混乱の多くは、質問が組み立てられたときに、ホストが車がどこにあるかを知っていて、常に最初にヤギを明らかにすることが誤って明確にされていないことが多いためです. 私は責任のいくつかを置くと思います マリリン ヴォス サバント, 彼女のコラムで質問をひどく組み立てた. 賞品がドア 1 の後ろにあると仮定しましょう。プレーヤー (2 番目の競技者) が切り替えない戦略を持っていた場合、次のようになります。
- プレーヤーがドア 1 を選択 --> プレーヤーの勝ち
- プレーヤーがドア 2 を選ぶ --> プレーヤーが負ける
- プレーヤーがドア 3 を選ぶ --> プレーヤーが負ける
以下は、プレーヤーが切り替えの戦略を持っていた場合に何が起こるかです。
- プレーヤーがドア 1 を選択 --> ホストがドア 2 または 3 の後ろにヤギを表示 --> プレーヤーが別のドアに切り替える --> プレーヤーが負ける
- プレイヤーがドア 2 を選ぶ --> ホストがドア 3 の後ろにいるヤギを明らかにする --> プレイヤーがドア 1 に切り替える --> プレイヤーが勝つ
- プレイヤーがドア 3 を選択 --> ホストがドア 2 の後ろにヤギを出現させる --> プレイヤーがドア 1 に切り替える --> プレイヤーの勝利
したがって、プレーヤーを切り替えないことで、勝つチャンスは 1/3 になります。 プレーヤーを切り替えることで、2/3 の確率で勝つことができます。 したがって、プレイヤーは間違いなく切り替える必要があります。
モンティ ホールのパラドックスの詳細については、ウィキペディア の記事をお勧めします。
- プレイヤーはドア1を選び、2が表示される。3に切り替えて負ける。
- プレイヤーはドア1を選び、3が表示される。2に切り替えて負ける。
- プレイヤーはドア2を選び、3が表示されると、1に切り替えて勝利する。
- プレイヤーはドア3を選び、2が表示されると、1に切り替えて勝利する。
ご覧の通り、切り替えるかどうかに関わらず勝率は50%です。しかも、切り替えた方が良いというのは常識に反しています。
これらの事象のそれぞれが25%の確率で発生すると想定するのは間違いです。正しい確率は以下の通りです。
- プレイヤーがドア1を選ぶ(1/3)* 表示されているドア2(1/2)= プレイヤーの負け(1/6)
- プレイヤーがドア1を選ぶ(1/3)* 表示されているドア3(1/2)= プレイヤーの負け(1/6)
- プレイヤーがドア2を選ぶ(1/3)* 表示されているドア3(1/1)= プレイヤーの勝利(1/3)
- プレイヤーがドア3を選ぶ(1/3)* 表示されているドア2(1/1)= プレイヤーの勝利(1/3)
したがって、負けるイベントの合計確率は 2*(1/6) = 1/3 となり、勝つイベントの合計確率は 2*(1/3) = 2/3 となります。
5 種類のトッピングから選べる場合、トッピングの数に応じて、何種類のピザを作ることができますか?
トッピングが0個の場合は1通り、1個の場合は5通り、2個の場合は10通り、3個の場合は10通り、4個の場合は5通り、5個の場合は1通りです。したがって、答えは1+5+10+10+5+1 = 32です。別の解き方としては、トッピングの有無で答えることもできます。つまり、合計は2 5 = 32です。
先週の新聞で、インドネシアを襲った最新の地震が12月26日に発生したと読みました。また、過去100年間で最も死者数の多い地震8件のうち、3件が12月26日に発生していることも報じられていました。このマグニチュード(マグニチュード8.0以上)の地震は年に一度しか発生しないという事実を踏まえると、同じ日に3つの巨大地震が発生する確率はどれくらいなのでしょうか? 前回の大地震はちょうど1年前の2003年12月26日にイランで発生しました(連続して発生する確率でしょうか?)。ご意見をお待ちしております。
フロリダのハリケーンがブッシュ氏の支持を得た郡にのみ襲来したという主張がデマだったと知り( 2004年10月17日のコラム参照)、私はこうした偶然の一致説にますます懐疑的になるつもりです。国立地震情報センターによると、1990年以降の地震のトップ11のうち、最近の地震は2004年の12月26日に発生したものだけです。あなたが言及したイランの地震はマグニチュード6.7で、トップ8にも遠く及びません。
毎日卵の半分と卵の半分を売って、3日後に卵が0個になった場合、最初の卵は何個になりますか? 毎日の終わりには、卵の数は整数になります。
一日の始まりの卵の数をd(昼)、終わりの卵の数をn(夜)としましょう。問題文からd/2 - ? = nと分かります。そこで、dをnで解いてみましょう。
d/2 = n + ?
d=2n+1
したがって、3日目にはn=0、d=1になります。
2日目はn=1なので、d=3になります。
3日目はn=3なので、d=7になります。
ということで、7 個の卵から始めました。
10人が住む島を想像してみてください。毎日、島民の1人がランダムに選ばれ、ちょうど1日だけ酋長を務めます。そして、その日が過ぎると、別の島民がランダムに選ばれます(つまり、酋長だった同じ島民が再び酋長になる確率は10分の1です)。ここで解くべき問題は、各島民が少なくとも一度は酋長を務めるには、平均して何日かかるかということです。
1人が酋長を務めるには1日しかかかりません。2日目に新しい酋長が誕生する確率は0.9です。毎日の確率が0.9の場合、新しい酋長が誕生するまでにかかる期待日数は1/0.9 = 1.11です。これはあらゆる確率に当てはまります。成功までの期待試行回数は1/pです。したがって、2人が酋長を務めた後、翌日に新しい酋長が誕生する確率は0.8です。したがって、3人目の酋長が誕生するまでの待機期間は1/0.8 = 1.25日です。答えは待機期間の合計で、1/1 + 1/.9 + 1/.8 + ... + 1/.1 = 29.28968日となります。
円の半径は1です。三角形は正三角形です。それぞれの色の領域の面積を求めましょう。
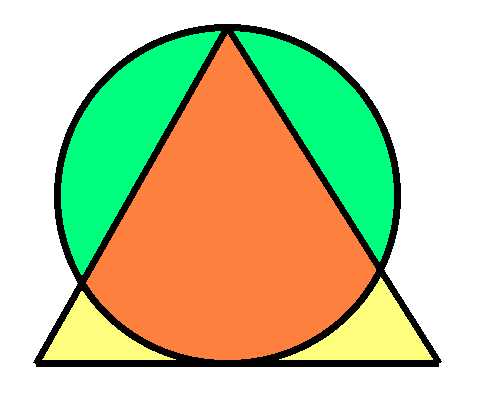
自分で解きたい人のために、答えを伏せたくありません。解答と解説は、私の別のウェブサイトmathproblems.info の問題189をご覧ください。
NBAの試合のハーフタイムにフリースローを1本打つコンテストで優勝したとしましょう。成功すれば賞金100万ドルが手に入ります。さらに、フリースローは2本投げるか投げないかのどちらかで、ミスするかやめるまで投げ続けることができます。もしフリースロー成功率が75%だとしたら、いつ止めますか?止められるでしょうか?ある時点で、お金の価値はどんどん薄れていきます。あなたならどうしますか?
賭け金が高すぎる場合、ある時点で良い賭けを断るべきです。個人的には、お金から得られる喜びを測る良い方法は、金額の対数を取ることだと考えています。対数の底は重要ではないので、10 を使いましょう。ただし、10 未満の対数は取れないので、10 未満の金額に対する喜びは 0 としましょう。つまり、あなたの例では、最初のスローで 1,000,000 ドルを獲得する前は $0 だったと仮定しましょう。これで、log(1,000,000) = 6 単位の幸福が得られます。もう一度フリースローをした場合の幸福の期待値は、0.75*log(2,000,000) + 0.25*0 = 4.975772 です。これは 6 より小さいので、この場合は 100 万ドルを受け取って立ち去るべきです。ただし、すでにいくらかのお金を持っている場合は状況が変わるかもしれません。すでに 200,000 ドルを持っているとしましょう。すると、賭けを放棄した場合の幸福度はlog(1,200,000) = 6.07918となります。100万ドルを賭けてもう一度賭けた場合の幸福度は、0.75*log(2,200,000) + 0.25*log(200,000) = 6.082075となり、かろうじて2回目の賭けに賭けることになります。もし2回目の賭けに勝った場合、選択肢はlog(2,200,000) = 6.34242と0.75*log(4,200,000) + 0.25*log(200,000) = 6.29269のどちらかになります。この場合、3回目の賭けはせず、200万ドルの勝利を手にして賭けを放棄するべきです。最初のダブル当選を受け入れるための損益分岐点は、既存の資産191,487ドルです。2回目のダブル当選を受け入れるには、他に382,975ドルの資産が必要です。
22人が同じ部屋にいたら、同じ誕生日(年ではなく月日)の人が2人いる確率は50%だと覚えています。それを証明する計算方法を忘れてしまいました。教えていただけますか?
以前にも答えたことがあると思いますが、50/50のポイントは23に近いです。話を単純にするために、うるう年は無視しましょう。長い答えは、23人を何らかの方法で順序付けすることです。人#2が人#1と誕生日が異なる確率は364/365です。人#3が人#1と人#2の誕生日とは異なる確率は、彼らが互いに異なると仮定すると、363/365です。これを23人目まで繰り返します。確率は(364/365)*(363/365)*...*(343/365) = 49.2703%です。つまり、一致しない確率は49.27%、少なくとも1人は一致する確率は50.73%です。もう 1 つの解は、23 個の異なる誕生日の順列の数を、1 から 365 までの 23 個の乱数を選択する方法の総数で割ることです。これは、 permut (365,23)/365 23 = 42,200,819,302,092,400,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 / 85,651,679,353,150,300,000,000,000,000,000,000,000,000,000,000,000,000,000 = 49.27% となります。
ある州の教師の週給は、平均490ドル、標準偏差45ドルの正規分布をしています。無作為に選ばれた教師が週給525ドル以上を稼ぐ確率はどれくらいでしょうか?母集団を考慮せずに、平均値と標準偏差だけから確率を計算する方法がわかりません。
これは平均より35ドル、つまり標準偏差7/9ドル高いことになります。期待値より標準偏差7/9ドル以上高い確率は、1-Z(7/9) = 1-0.78165 = 0.21835となります。
二人でじゃんけんをしています。このゲームには戦略は関係ないと仮定します。「3本勝負」で、プレイヤーAが最初のラウンドに勝った場合、プレイヤーBが勝つ確率はどれくらいでしょうか?
プレイヤー B は次の 2 試合に勝つ必要がある (引き分けは除く) ため、確率は (1/2)*(1/2) = 1/4 になります。
こんにちは。ウェブ上でもなかなか見つからないので、質問させてください。答えていただけたら嬉しいです。私たちが存在する確率はどれくらいでしょうか?地球上でも、宇宙のどこか他の場所でも同じです。これはギャンブル的な質問ではありませんが、私たち全員が知っておくべき答えです。そうすれば、生きているだけでどれほどの確率を乗り越えられるか、理解できるはずです。
銀河系のどこかに知的生命体が存在する確率は非常に高いと私は考えています。ドレイクの方程式は、銀河系における知的生命体の出現数を推定しようとするもので、数値によっては100万程度という数字が出ます。しかし、これらの文明が地球を訪れたり、接触したりしたという確かな証拠もありません。有名なフェルミの問いは「みんなどこにいるのか?」です。他の知的生命体の証拠がないことはドレイクの方程式に疑問を投げかけるかもしれませんが、それでも私たちの銀河系に存在する知的文明の数は1000程度だと考えます。これは私たちの銀河系だけで、宇宙には数十億もの銀河があります。しかし、銀河間の距離は非常に大きいため、銀河間の移動や通信について議論してもあまり意味がありません。ですから、あなたの質問に答えるとすれば、およそ99.9%でしょう。
あるホテルに1000万室の客室と1000万個の電子キーがあるとします。コンピューターのミスにより、各キーにはランダムなコードがプログラムされており、そのコードが正しい確率は1000万分の1です。ホテルは満室です。有効なキーを持っている宿泊客が少なくとも1人いる確率はどれくらいでしょうか?
正確な答えは、1-(9,999,999/10,000,000) 10,000,000 = 0.632121です。これは小数点以下7桁まで(e-1)/eと同じです。
試験には75問の多肢選択問題があります。各問題には4つの選択肢があり、正解は1つだけです。合格点は50%です。各解答を推測して合格する確率はどれくらいでしょうか?
635,241 分の 1。
インランニングベッティングの場合、テニス選手がゲームに勝つチャンスが「p」あるとすると、セットに勝つチャンスはどれくらいでしょうか?
テニスのルールを理解している限り、セットの勝者は6ゲームを先に勝ち、かつ2ゲーム以上の差をつけたプレイヤーです。ただし、6-6の同点の場合は、タイブレーカーゲームが1つ発生します。以下の表は、ゲームに勝つ確率を前提として、セットに勝つ確率を示しています。
テニスにおける確率
| 確率 ゲーム勝利 | 確率 セット勝利 |
| 0.05 | 0.000003 |
| 0.1 | 0.000189 |
| 0.15 | 0.001899 |
| 0.2 | 0.009117 |
| 0.25 | 0.028853 |
| 0.3 | 0.06958 |
| 0.35 | 0.138203 |
| 0.4 | 0.23687 |
| 0.45 | 0.361085 |
| 0.5 | 0.5 |
| 0.55 | 0.638915 |
| 0.6 | 0.76313 |
| 0.65 | 0.861797 |
| 0.7 | 0.93042 |
| 0.75 | 0.971147 |
| 0.8 | 0.990883 |
| 0.85 | 0.998101 |
| 0.9 | 0.999811 |
| 0.95 | 0.999997 |
ゲームpに勝ち、ゲームqに負ける確率の式は、1*p 6 + 6*p 6 *q + 21*p 6 *q 2 + 56*p 6 *q 3 + 126*p 6 *q 4 + 252*p 7 *q 5 + 504*p 7 *q 6です。
あなたは淡水湖で、岩を載せたボートに乗っています。岩を湖に投げ入れます。陸地(岸)を基準にすると、水位は上昇しますか、下降しますか、それとも一定のままですか?同僚たちは水位は一定のままだと考えています。
岸に対する水位は低下します。ボートの中では、岩がカヌーを押し下げ、周囲の水を押し上げています。押しのけられる水の量は、岩の重さと等しくなります。例えば、10ポンドの岩は、10ポンドの水を上方に押し上げます。岩を船外に投げ出す場合、重さではなく、岩の体積が重要になります。つまり、岩は岩と同じ体積の水を押し上げます。岩の質量は水の質量よりも大きいため、岩は岩の中にある水よりも、岩を押し下げる水のほうが多く押しのけます。そのため、湖の水位は、岩がカヌーの中にある場合の方が、湖底にある場合よりも高くなります。
これはどのように作動しますか?
- 電卓を用意してください。(これは頭の中では計算できません)
- 電話番号の最初の3桁を入力してください(市外局番ではありません)
- 80倍する
- 1を追加
- 250倍する
- 電話番号の下4桁を追加してください
- 電話番号の最後の4桁をもう一度追加します。
- 250を引く
- 数を2で割る
答えは分かりますか?
あなたの電話番号の最初の3桁をx、最後の4桁をyとしましょう。それでは、各ステップで何が得られるか見ていきましょう。
- 準備ができて!
- X
- 80倍
- 80倍+1
- 250*(80x+1) = 20000x+250
- 20000x+250+y
- 20000倍+250+2年
- 20000x+250+2y-250 = 20000x+2y
- (20000x+2y)/2 = 10000x+y
これはもちろんあなたの電話番号と同じになります。10000x を使ってプレフィックスを4桁左に移動し、最後に最後の4桁を足します。
27,000ドルの車が当たる抽選があり、6枚で500ドル、または1枚で100ドルで販売されています。すでに68枚のチケットが売れており、明日が購入期限です。当選確率を50%にするには5,666.44ドル、当選確率を66.66%にするには11,332.88ドルを支払う必要があることは分かっています(合っていますか?)。車をほぼ確実に「当てる」には、いくら支払えば(あるいは何枚のチケットを買えば)いいでしょうか?(90%?95%?)この抽選に参加する価値はあるのでしょうか?それとも、車代金を支払わなければならないのでしょうか?
1/2と2/3の確率については、おっしゃる通りです。t枚のチケットを購入した場合、当選確率はt/(68+t)です。つまり、90%の確率を求めるには、tについて以下のように解く必要があります。
0.9 = t/(68+t)
0.9*(68+t) = t
61.2 = 0.1トン
t = 612、または51,000ドル
95% の場合...
0.95 = t/(68+t)
0.95(68+t) = t
64.6 = 0.05トン
t = 1292、または107,666.67ドル
その車があなたにとって 27,000 ドルの価値があると仮定すると、次に販売されるチケットの価格に見合うだけの当選確率が上がらなくなったら、すぐにチケットの購入をやめるべきです。
チケットが価格に見合う価値があるためには、当選確率が p 増加する必要があり、ここで...
27000*p=(500/6)
p=0.003086
t は、もう 1 枚チケットを購入しても構わない場合に購入したチケットの数だとします。
[(t+1)/(t+68+1)] − [t/(t+68)] = 0.003086
[(t+1)/(t+69)] − [t/(t+68)] = 0.003086
[((t+1)*(t+68))/((t+69)*(t+68))] − [(t*(t+69))/((t+68)*(t+69))] = 0.003086
[((t 2 +69t+68)/((t+69)*(t+68))] − [(t 2 +69t)/((t+68)*(t+69))] = 0.003086
68/((t+68)*(t+69)) = 0.003086
((t+68)*(t+69)) = 220.32
t 2 +137t+4692 = 22032
t 2 +137t - 17340=0
t=(-137+/-(137 2 -4*1*-17340) 2 )/2
t = 79.9326
プレイヤーが常にチケットを 1 枚あたり $500/6 = $83.33 で購入できると仮定して、購入したチケットの値を入力してこれをテストしてみましょう。
79 枚のチケットの場合、コストは 79*(500/6) = 6,583.33 ドル、当選確率は 79/(79+68) = 53.74%、期待収益は 27,000*0.5374 = 14,510.20 ドル、期待利益は 14,510.20 ドル - 6,583.33 ドル = 7,926.87 ドルとなります。
80枚のチケットの場合、費用は80*(500/6) = 6,666.67ドル、当選確率は80/(80+68) = 54.04%、期待リターンは27,000*0.5405 = 14,594.59ドル、期待利益は14,594.59 - 6,666.67 = 7,927.92ドルとなります。
81 枚のチケットの場合、コストは 81*(500/6) = 6,750.00 ドル、当選確率は 81/(81+68) = 54.36%、期待収益は 27,000*0.5436 = 14,677.85 ドル、期待利益は 14,594.59 ドル - 6,750.00 ドル = 7,927.85 ドルとなります。
したがって、予想される最大の勝利は 80 枚のチケットでピークに達することがわかります。
電気代を節約するために、古い冷蔵庫を今買い替える場合と、壊れるまで待ってから買い替える場合のコストを比較しようとしています。新しい冷蔵庫と古い冷蔵庫のどちらが稼働率が下がるか計算できます。年間 37 ドルです。これは簡単です。しかし、新しい冷蔵庫のコストをどう計算に入れればよいでしょうか。新しい冷蔵庫が 425 ドルだとします。その 425 ドルの *すべて* が新しい出費だとは言えません。なぜなら、今でなくてもいつかは古い冷蔵庫を買い替える必要があり、いずれにしても新しい冷蔵庫の出費はいつか発生するからです。一般的な冷蔵庫の耐用年数は 14 年で、古い冷蔵庫は 9 年前のものだとします。つまり、今買い替えると 5 年後に買い替えることになります。今使っている冷蔵庫を9年間使ってから買い替える場合と、今買い替える場合の費用を比較する2列の表を作ろうとしたのですが、どれくらい先の費用を考えれば良いのかわからず、冷蔵庫の買い替え時期もそれぞれ異なるため、どう比較すればいいのか分かりませんでした。今買い替える場合と後で買い替える場合の経済性をどのように比較すれば良いのでしょうか?ちなみに、これは私自身のケースではありません。今の冷蔵庫はおそらく30年ほど前のものです。これは、友人のためのものです。
現在の冷蔵庫を使い続けると、5年後には新しい冷蔵庫を買った場合と比べて、電気代に37ドル×5ドル=185ドル余計にかかることになります。今買い替えると425ドルの損失になりますが、5年後の減価償却を想定すると、425ドル×(9/14)=273.21ドルの価値が残ります。つまり、減価償却によって425ドル×(5/14)=151.79ドルの損失が出ることになります。つまり、新しい冷蔵庫の減価償却費は、古い冷蔵庫を使い続けることで発生する追加の電気代よりも低いので、私は今すぐ新しい冷蔵庫を買うことを推奨します。
3 人いる場合、少なくとも 2 人が同じ日に誕生日を迎える確率はどれくらいですか。
閏日を無視すると、3つの異なる誕生日の確率は(364/365)*(363/365) = 0.99179583です。したがって、少なくとも1つの誕生日が共通する確率は1 - 0.99179583 = 0.00820417です。
5人が同じ部屋にいます。そのうち少なくとも2人が同じ誕生月に生まれた確率はどれくらいですか?
話を単純にするために、各人が各月に生まれる確率は1/12だと仮定しましょう。5人全員が異なる月に生まれる確率は(11/12)*(10/12)*(9/12)*(8/12) = 0.381944です。つまり、同じ月に生まれる確率は1 - 0.381944 = 0.618056です。
職場でちょっとした遊びでチャレンジを与えられたのですが、誰も答えられません。ある農家が羊を満載したトレーラーを5台所有しています。4台には39kgの羊が、5台目には40kgの羊がいます。羊たちは皆同じ種類です。彼は市場へ行き、どのトレーラーに40kgの羊が乗っているかを調べたいのですが、大きな体重計は一度しか使えません!一体どうやって調べるのでしょう?助けてください。私の職場は獣医なのですが、みんな頭にきています!
答えはコラムの最後にあります。
羊に関する質問への答え
トレーラー 1 から羊を 1 匹、トレーラー 2 から 2 匹、トレーラー 3 から 3 匹、トレーラー 4 から 4 匹、トレーラー 5 からは 0 匹取り出します。羊全体の重量が 39 kg の場合、合計重量は 39 * 10 = 390 kg になります。ただし、0 匹から 4 匹の羊は 1 kg 重いです。合計重量が 391 の場合、秤には重い羊が 1 匹いることになり、その羊はトレーラー 1 から来たに違いありません。同様に、合計重量が 392 の場合、秤には重い羊が 2 匹いることになり、その羊はトレーラー 2 から来たに違いありません。同様に、重量が 393 は重い羊がトレーラー 3 にいることを意味し、重量が 394 は重い羊がトレーラー 4 にいることを意味し、重量が 390 は重い羊がトレーラー 5 にいることを意味します。
180 席もある飛行機で、同じ便に乗る美人の隣に座れる確率はどれくらいでしょうか?
クラスター内の座席数によって異なります。ほとんどの国内線では、通路の両側に3席ずつあります。つまり、3席ずつのクラスターが60個あります。最初の1人が着席すると、残りの179席のうち2席が同じクラスターになります。つまり、同じクラスターになる確率は2/179 = 1.12%です。つまり、中央の席に他の人が座ることはありません。3人目が中央の席に座る確率は1/3です。つまり、答えは(2/179)*(2/3) = 0.74%、つまり134.25分の1です。
3人の論理学者がゲームをしています。各自が正の整数を秘密裏に書き出さなければなりません。最も小さい整数を書いた論理学者が3ドルを獲得します。3人全員が同じ数字を書いた場合は、それぞれが1ドルを獲得します。論理学者たちは利己的で、それぞれが自分の利益を最大化しようとします。意思疎通は禁止されています。各論理学者はどのような戦略を取るでしょうか?
答えは次のコラムに表示されます。
ウォーレン・バフェット(世界第3位の富豪)が、自分は連邦税率17.7%しか払っていないのに、秘書は30%も払っていると不満を漏らしたと読んだことがあります。これはとんでもない話だと思います。何かご意見はありますか?
通常なら、これは私の専門外だと言うところです。しかし、8年間政府のアクチュアリーとして働いてきた経験から、税金については多少の知識があります。私が読んだところによると、ウォーレン・バフェット氏の収入の大部分はキャピタルゲインとして定義されており、税率はわずか15%です。好むと好まざるとにかかわらず、税法はそれを容認しています。私が不思議に思ったのは、なぜ彼の秘書が30%もの税金を支払っていたのかということです。このビデオによると、彼は「給与税と所得税」を数えていました。「給与税」とは、明らかに社会保障税とメディケア税のことです。彼の秘書にとって、30%という連邦税率が妥当な金額なのかどうか、見てみましょう。
2007年、最高税率区分は35%でしたが、これは349,700ドルを超える所得にのみ適用されます。それ以下の所得には、はるかに低い税率が適用されます。彼の秘書は独身で、扶養家族はおらず、給与は100,000ドルだったと仮定しましょう。まず、最低控除額を差し引きます。2007年、独身申告者の標準控除額は5,350ドルでした。個人控除額は3,400ドルでした。つまり、100,000ドル - 5,350ドル - 3,400ドル = 91,250ドルが所得税の対象となる所得となります。2007年の独身申告者の場合、最初の7,825ドルまでの所得に対する税率は10%、31,850ドルまでは15%、77,100ドルまでは25%、160,850ドルまでは28%でした。つまり、彼女の所得税は0.1×7,825ドル+0.15×(31,850ドル-7,825ドル)+0.25×(77,100ドル-31,850ドル)+0.28×(91,250ドル-77,100ドル)=19,660.75ドルとなります。これは彼女の収入のわずか19.7%です。彼女の収入、申告方法、項目別控除の有無といった私の仮定はすべて、彼女に不利に働き、税率を高くしました。
では、社会保障税とメディケア税について考えてみましょう。2007年の社会保障税は、所得が97,500ドルを超えると完全に免除される6.2%でした。2007年のメディケア税は1.45%で、上限はありませんでした。つまり、彼女の社会保障税とメディケア税を合わせた税率は、6.2%×97,500ドル + 1.45%×100,000ドル = 7,495ドルでした。これらの税金を加えると、彼女の全体の税率は(19,660.75ドル + 7,495ドル)÷100,000ドル = 27.2%になります。それでも、30%には2.8%足りません。
彼女は、最終的には雇用主が負担する社会保障税とメディケア税も自分が負担することになるという事実も考慮しているのではないかと思います。ご存知ない方のために説明すると、社会保障税とメディケア税は実際には給与から差し引かれる金額の2倍です。雇用主は残りの半分を支払います。しかし、私を含め、中には最終的には従業員が両方を支払うべきだと主張する人もいます。雇用主がその税金を払わなくても済むなら、従業員に支払うお金が増えるはずです。私のように自営業で両方の負担を強いられていると、そう感じてしまうのは当然です。社会保障税とメディケア税を2倍にすると、税率は(19,660.75ドル + 2×7,495ドル)/ 100,000ドル = 34.7%になります。4.7%の差は、彼女の収入が100,000ドル未満、結婚している、扶養家族がいる、控除項目を明記している、あるいはそれらの組み合わせが理由だと思います。
社会保障税とメディケア税は、ウォーレン・バフェット氏にはほとんど影響しません。第一に、社会保障の上限額である9万7500ドルは彼にとって取るに足らないものです。第二に、これらの税金は給与に適用されるものであり、彼が収入の大部分と定義しているキャピタルゲインには適用されません。
これが、バフェット氏の発言の背後にある計算についての私の最善の推測です。
追記:このコラムが掲載されて間もなく、以下の反論をいただきました。公平を期すため、バフェット氏は税金を払い過ぎているという主張を以下に提示します。
ウォーレン・バフェット氏が秘書よりも低い税率で納税していることは不公平だと「憤慨」している方へのあなたの回答を興味深く拝読しました。バフェット氏が秘書よりも低い税率で納税しているという誤った情報を覆すような回答には、全く失望しました。まず、ご指摘のとおり、投資所得には確かに15%の税金が課せられます。これは事実上、二重課税です。バフェット氏が投資した稼得所得には、彼の限界税率である36%が課せられていたのです。まるでリンゴとオレンジ(労働所得と投資所得)を比較しているようなものです。
第二に、パーセンテージを見るべきではありません。ギャンブルで言うなら、「配当」を見るべきです。バフェット氏が数百万ドルもの税金を支払ったのと同じ年に、彼の秘書が数千ドルを納税したと確信しています。読者は、国民一人が他の国民の何千倍もの税金を同じ政府サービスに支払っていることに、もっと憤慨すべきではないでしょうか?「ウォーレン・バフェットは秘書の100万倍もの税金を払っていると聞きました。とんでもない!」と簡単に言うこともできるでしょう。
「実際の配当」ではなく「パーセンテージ」だけを見るのは誤りだと指摘しておきます。あなたがギャンブルでよく言う誤りと似ていますね。
よろしくお願いします、
ケビン・A(ダラス)
楽しい数学パズル集をありがとうございます。彼女と海賊パズルのバリエーションを思いつきました。もし海賊全員が同じ階級で、各ラウンドで分割案を提案する人がくじ引きで選ばれたらどうなるでしょうか?このバリエーションでは、各海賊の最優先事項は、受け取るコインの期待値を最大化することだと仮定します。私は解法だと思うのですが、まずはご自身で試してみてはいかがでしょうか。重ねてお礼申し上げます。
どういたしまして。もし海賊が2人しか残っていない場合、提案をするために選ばれた方はもう1人が反対票を投じるので、もう1人が提案を諦めざるを得ません。抽選で選ばれた方は0枚、もう1人は1000枚獲得します。つまり、抽選前、残り2人の海賊の期待値は500枚です。
3人の海賊の段階では、引かれた海賊は他の海賊の1人に501と499を自分に渡すことを提案します。501を引いた海賊は、500をノーと投票した場合の期待値よりも大きいため、賛成票を投じます。引き分け前、残り3人の海賊の場合、0、499、501のコインがそれぞれ1/3の確率で手に入るため、平均333.33になります。
4人の海賊の段階では、引かれた海賊は他の海賊のうち2人に334を、そして自分に332を渡すことを選択します。これにより、334枚のコインを受け取る海賊から2票の「賛成」票が得られます。なぜなら、彼らは333.33よりも334枚の方が欲しいからです。あなた自身の票を含めると、4票中3票を獲得することになります。引く前の各海賊の期待値は、0、334、334、332の平均、つまり1000/4=250です。
同じ論理で、5人の海賊の段階では、引かれた海賊は251を2人の海賊に、そして498を自分自身に与えることを選択します。最初の問題とは異なり、逆算する必要はありません。コインの枚数を、自分を除く海賊の枚数で割るだけです。そして、その平均値と、さらに1枚のコインを海賊の半数(端数切り捨て)に渡します。
「Eternity II」というパズルの攻略法を教えていただきたいです。このパズルを解くとなんと200万ドルという高額な賞金がもらえます。私にとってはかなりの金額です。ゲーム開発者のクリストファー・モンクトン氏(マーガレット・サッチャー元首相の顧問など、様々な経歴を持つ)のインタビューへのリンクはこちらです。このゲームはギャンブルとは全く関係ないのは明らかですが、それでも、あなたのウェブページに一言二言、このゲームについて書いていただけると嬉しいです。
上のリンクで、ゲーム制作者はこのパズルが解けないと豪語しています。彼の言う通りで、この(馬鹿げているけれど魅力的な)ゲームを売って最終的に金持ちになるのは彼だけなのではないかと考え始めています。数学者であるあなたは、このようなパズルをどうやって解くのでしょうか?
皆さんが幸せだといいのですが。ここ1ヶ月ほど、このパズルに夢中になっています。256ピースのパズルは地元のボーダーズ書店で見つけたのは幸運(というか不運)だったのですが、ヒントパズル4つはeBayでオーストラリアの人から買わなければなりませんでした。
4つのヒントパズルを簡単に解けるプログラムを書きました。72ピースのヒントパズル4番を1秒もかからずに解けました。やり方は、単純な総当たり再帰プログラムです。ボードの境界線から始めて、ボード上にパスを描きます。各位置で、プログラムは未使用のピースをすべてループし、合うピースを探します。ピースが見つかったら次のマスへ、見つからなければ1マス戻ります。
2台のコンピューターに256ピース、200万ドルのパズルを何週間もかけて解かせてきましたが、どちらも全く及ばない。あの動画の作者が言っていたことには、私も同感だ。世界最速のコンピューターを1000万台繋いでも、宇宙が消滅するまでには解けないかもしれない、と。始める前に彼の警告に耳を傾けるだろうと思うかもしれないが、良いパズルを前にすると、時間の有効活用などどうでもよくなってしまう。
ショートカットのアイデアはたくさんあるのですが、たとえプログラムを10億倍高速化したとしても、おそらく効果はないと思います。もし誰かがこのパズルを解いてくれたら、本当に感激するでしょう。本当に気になるのは、このようなパズルを簡単に解ける、まだ発見されていない数学の分野があるのではないかと思うことです。それまでは、試行錯誤を繰り返すのが精一杯だと思います。今のコンピューターは遅すぎるし、組み合わせの数も膨大すぎるので、うまくいく可能性は低いでしょう。

2つの都市間の距離が1,000マイルだとします。無風状態では、飛行機は時速500マイルで飛行できます。無風の場合と、片方向に時速100マイルの追い風、反対方向に同じ速さの向かい風が吹いている場合では、往復にかかる時間はどちらが長くなりますか?
無風の場合、片道2時間で、合計4時間かかります。追い風の場合、飛行機は時速600マイルで飛行し、1000/600 = 1.667時間かかります。向かい風の場合、飛行機は時速400マイルで飛行し、1000/400 = 2.5時間かかります。つまり、風がある場合、合計時間は4.167時間、つまり10分長くなります。
これは、平均値を平均化することが危険であることを示しています。片道が時速400マイル、反対側が時速600マイルの場合、平均速度が時速500マイルとは言えません。時速400マイルの区間の方が長い期間にわたっているからです。
これが直感的に分かりにくい場合は、時速500マイル(約800キロメートル)の風を考えてみてください。風だけで飛行機は1時間で移動しますが、逆方向だと止まってしまい、永遠にかかることになります。
最近、7,033個の賞品がある抽選に参加しました。当選確率は13分の1だそうです。5枚購入しました。当選確率は実際どれくらいでしょうか?また、高額賞品が40個あるのですが、高額賞品が当たる確率はどれくらいでしょうか?
話を簡単にするために、チケットを多く買えば買うほど、自分自身と競争することになるため、1枚あたりの価値が下がるという事実は無視しましょう。とはいえ、5枚のチケット全てが外れてしまう確率は(12/13) 5 = 67.02%です。つまり、少なくとも1つの賞品が当たる確率は32.98%です。購入前のチケットは合計7033×13=91,429枚あります。そのうち91,429-40=91,389枚は高額賞品ではありません。5枚のチケットで高額賞品が1つも当たらない確率は(91,389/91429) 5 = 99.78%です。つまり、少なくとも1つの高額賞品が当たる確率は0.22%、つまり458分の1です。
数ヶ月前から解こうとしているパズルがあるのですが、全く進展がありません。時間があれば、どうかお付き合いいただけたら嬉しいです。夜も眠れないほど悩んでいるんです :-)。ところで、 『Beyond Counting -- Exhibit CAA』の用語集には、「マジックナンバー」という用語として、3つの数字と文字の並びが挙げられています。そのうちの1つは本の表紙にも使われているので、何か重要な意味を持っているのだと思います。何かご意見はありますか?
普段はあまり言わないのですが、全く分かりません。別のメールでもご指摘いただいたように、アメリカ紙幣のシリアルナンバーと同じ形式で、2文字のアルファベットと10桁の数字が間に入っています。著作権保護のため、ここでは数字は明記しません。
Eternity IIのパズルチャレンジはどうなったのか気になります。解決しましたか?まだ取り組んでいますか?
質問ありがとうございます。いえ、 2008年11月17日の「Ask the Wizard」コラムで書いた以来、その件には触れていません。彼らのウェブサイトによると、2009年12月31日と、必要に応じて2010年12月31日に「精査日」を設けるとのことです。私の意見では、これは永遠に解決されないでしょう。
更新: Eternity II の Web サイズはもう存在しないようです。
アーノルド・シュワルツェネッガーの拒否権発動に関するウィザードのブログを興味深く読みました。私の質問は、知事のばかばかしくも予想通りの反応についてです。知事は「単なる偶然」だと述べました。圧倒的な状況証拠(法案の提案者と拒否権発動の手紙の宛先は、1週間前に知事に暴言を浴びせた人物でした)があるにもかかわらず、7行の手紙の中に偶然このフレーズが綴られている確率はどれくらいだと思いますか?使用されている文字を考慮すると、それぞれ26分の1の確率を割り当てるよりもさらに低いと思います。U、Y、そして特にKは、単語の頭文字としてはあまり一般的ではないようです。
気分を害しやすい方は、次の質問に進んでください。
そのブログを読んでいない読者のために、カリフォルニア州知事アーノルド・シュワルツェネッガーのメモ (PDF)の各行の最初の文字を、文字 F で始まる行から見てください。
この件については、私の関連サイト「Wizard of Vegas」で議論されました。答えを見つけるために、 Wikipediaで英語の単語の最初の文字の出現頻度を調べました。
最初の文字による単語の頻度
| 手紙 | 頻度 |
| あ | 11.60% |
| B | 4.70% |
| C | 3.51% |
| D | 2.67% |
| E | 2.00% |
| F | 3.78% |
| G | 1.95% |
| H | 7.23% |
| 私 | 6.29% |
| J | 0.63% |
| K | 0.69% |
| L | 2.71% |
| M | 4.37% |
| 北 | 2.37% |
| お | 6.26% |
| P | 2.55% |
| 質問 | 0.17% |
| R | 1.65% |
| S | 7.76% |
| T | 16.67% |
| あなた | 1.49% |
| V | 0.62% |
| W | 6.66% |
| X | 0.01% |
| はい | 1.62% |
| Z | 0.05% |
アーノルドのメッセージが単なる偶然であった確率を推定すると、Prob(F) × Prob(U) × ... × prob(U) = 0.0378 × 0.0149 × 0.0351 × 0.0069 × 0.0162 × 0.0626 × 0.0149 = 486,804,391,348分の1となります。この確率には、2つの単語間のスペースの代わりに都合よく改行が挿入されていたという事実すら考慮されていません。
この解決策に意見を提供してくれた Eliot J. と Jonathan F. に感謝します。
空港の手荷物受取所では、受け取る荷物の数が多ければ多いほど、すべての荷物が出てくるまで待つ時間が長くなります。荷物が1つなら、半分くらい出てくるまで待たなければなりません。荷物が2つなら待ち時間は長くなり、3つならさらに長くなります。私の荷物が他の荷物とランダムに混ざっていると仮定すると、私の荷物の数と荷物の総数から、すべての荷物を受け取るまでに待たなければならない荷物の数は、一般的にどのような計算式で求められますか?
まず、次のようにいくつかの変数を定義しましょう。
n = バッグの数
b = バッグ総数
バッグの総数が増えるにつれて、答えはb×n/(n+1)に近づきます。大型飛行機の場合、これで概算値が得られます。しかし、正確な値を知りたい場合は、答えは次のようになります。
[b× combin (b,n)-(combin(i,n)のi=nからb-1までの合計)]/combin(b,n)
例えば、合計10個のバッグがあり、そのうち4個があなたのバッグである場合、予想される待ち時間は次のようになります。
[10×コンビ(10,4)-コンビ(4,4)-コンビ(5,4)-コンビ(6,4)-コンビ(7,4)-コンビ(8,4)-コンビ(9,4)]/コンビ(10,4) = 8.8袋。
解決:
b個の袋からn個を取り出す方法はcombin(b,n)です。したがって、最初のx個の袋の中にすべての袋が出てくる確率はcombin(x,n)/combin(b,n)です。最後の袋がx番目に出てくる確率は、x>=n+1の場合、(combin(x,n)-combin(x-1,n))/combin(b,n)です。x=nの場合、1/combin(b,n)です。
したがって、予想待ち時間と合計待ち時間の比率は次のようになります。
n×combin(n,n)/combin(b,n) +
(n+1)×(combin(n+1,n)-combin(n,n))/combin(b,n) +
(n+2)×(combin(n+2,n)-combin(n+1,n))/combin(b,n) +
。
。
。
+
(b-1)×(combin(b-1,n)-combin(b-2,n))/combin(b,n) +
b×(combin(b,n)-combin(b-1,n))/combin(b,n)
伸縮合計を取ると、これは次のように簡略化されます。
[b×combin(b,n)-combin(b-1,n)-combin(b-2,n)-...-combin(n,n)]/combin(b,n)
後日、ある読者から、答えはn×(b+1)/(n+1)と簡略化できるというコメントをいただきました。これは帰納法という正当な方法で証明できるのですが、どうしても納得がいきません。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
私は彫刻を販売しています。平均すると、彫刻の売上7件のうち1件はカメで、残りは他の種類の彫刻です。今後100回の彫刻販売で在庫が切れない確率を90%にするには、カメの在庫を何個用意しておく必要がありますか?

製造されたタートルの数を t とし、販売された数を x とします。
pr(x<=t)=0.9
pr(x-14.29<=t-14.29)=0.9
pr((x-14.29)/3.5)<=(t-14.29)/3.5))=0.9
不等式の左辺は標準正規分布(平均0、標準偏差1)に従います。この次のステップを受け入れるには、統計学入門講座を受けるか、ある程度の信仰が必要です。
(t-14.29)/3.5 = normsinv(0.9) これはExcel関数です。
(t-14.29)/3.5 = 1.282
t-14.29 = 4.4870
t = 18.77
亀の像を0.77個買う人はまずいないでしょうから、19個に切り上げます。二項分布によれば、18個以下が売れる確率は88.35%、19個以下が売れる確率は92.74%です。この質問は、私の関連サイト「Wizard of Vegas」のフォーラムで提起され、議論されました。
5人の船員が難破船から生還しました。まず最初に、彼らはココナッツを集め、大きな山を作りました。その後、均等に分けるつもりでしたが、ココナッツを集める重労働で疲れ果てていました。そこで彼らは、朝になって山を分け合うつもりで、そのまま眠りにつきました。
しかし、船員たちは互いに信用し合っていない。真夜中、一人が目を覚まし、自分の分け前を取ろうとする。彼は山を5等分し、ココナッツを1つ残した。彼は自分の分を土に埋め、残りの4つの山をまとめて新たな共同の山を作り、残ったココナッツを猿に与えた。
午前 1 時、午前 2 時、午前 3 時、午前 4 時に、他の 4 人の船員もまったく同じことを行います。
朝になっても誰も自白せず、当初の計画通りココナッツの山を均等に分けることにした。するとまたしてもココナッツが一つ余り、彼らはそれを猿に与えた。
元の山にあるココナッツの最小の個数は何ですか?
「答えは100行下にスクロールしてください。」
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
元の山には15,621個のココナッツがありました。私の解答は、あと100行下にスクロールしてください。
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
元の山にあったココナッツの数を c とし、最後の分割後の各船員の最終的な取り分を f とします。
船員1が自分の分け前を取って猿にココナッツを与えると、(4/5)×(c-1) = (4c-1)/5が残ります。
船員2が自分の分け前を取って猿にココナッツを与えると、(4/5)×(((4c-1)/5)-1) = (16c-36)/25が残ります。
船員3が自分の分け前を取って猿にココナッツを与えると、(4/5)×(((16c-36)/25)-1) = (64c-244)/125が残ります。
船員4が自分の分け前を取って猿にココナッツを与えると、(4/5)×(((64c-244)/125)-1) = (256c-1476)/625が残ります。
船員5が自分の分け前を取って猿にココナッツを与えると、(4/5)×(((256c-1476)/625)-1) = (1024c-8404)/3125が残ります。
朝には、各船員の残りの山の取り分は f = (1/5)×(((1024c-8404)/3125)-1) = (1024c-11529)/15625 になります。
では、f=(1024×c-11529)/15625が整数となるようなcの最小の値は何か、という問いです。cをfを使って表してみましょう。
(1024×c-11529)/15625 = f
1024c - 11529 = 15625×f
1024c = 15625f+11529
c = (15625f+11529)/1024
c = 11+((15625×f+265)/1024)
c = 11+15×f+(265×(f+1))/1024
では、265×(f+1)/1024が整数となる最小のfは何でしょうか?265と1024には共通因数がないので、f+1は1024で割り切れる必要があります。f+1の最小値は1024なので、f=1023となります。
したがって、c = (15625×1023+11529)/1024 = 15,621となります。
各人および各サルが受け取ったココナッツの数は次のとおりです。
ココナッツ問題
| 船乗り | ココナッツ |
| 1 | 4147 |
| 2 | 3522 |
| 3 | 3022 |
| 4 | 2622 |
| 5 | 2302 |
| 猿 | 6 |
| 合計 | 15621 |
私にこの質問をぶつけてきたデイビッド・フィルマーは、既に答えを知っていました。実は彼は船員がs人という一般的な場合の式を尋ねたのですが、私は船員が5人という具体的なケースで十分苦労しました。デイビッドは、一般的な場合の答えは c = s s+1 - s + 1 だと指摘しています。
その証明は読者にお任せします。
この問題の代替解決策へのリンクをいくつか示します。
ある男性に、お金が詰まった2つの封筒が渡されます。片方の封筒には、もう片方の封筒の2倍の金額が入っています。男性が自分の封筒を選び、開けて中身を数えた後、もう片方の封筒と交換する選択肢が与えられます。問題は、封筒を交換することで男性に何か利益があるかどうかです。
封筒を交換することで、最初の封筒の金額が少ない場合は50%の確率でお金が2倍になり、最初の封筒の金額が多い場合は50%の確率で半分になるようです。したがって、最初の封筒に入っていた金額をx、封筒を交換することによる価値をyとすると、次のようになります。
y = 0.5×(x/2) + 0.5×(2x) = 1.25x
最初の封筒に100ドルが入っていたとしましょう。すると、もう一方の封筒に2 × 100ドル = 200ドルが入っている確率は50%、もう一方の封筒に(1/2) × 100ドル = 50ドルが入っている確率も50%になります。この場合、封筒の価値は次のようになります。
0.5×(100ドル/2) + 0.5×(2×100ドル) = 125ドル
つまり、封筒を交換するだけで、平均して彼の資産は25%も増加することになるのです!一体どういうことでしょうか?
これは数学的なパラドックスのように見えますが、実際には期待値の公式の乱用です。質問で指摘されているように、もう一方の封筒には、あなたが選んだ封筒よりも25%多く入っているはずです。しかし、もしあなたがその封筒を買うなら、最初からもう一方の封筒を選んだ方が賢明です。さらに、この議論を利用すれば、封筒を開ける前に切り替えを決めなければ、永遠に切り替え続けることができます。明らかに、期待値の議論には何らかの欠陥があるはずです。問題は、その欠陥がどこにあるのかということです。
長年にわたり、この問題について多くの時間をかけて読み、議論してきました。y=0.5x + 0.5*2x = 1.25xという議論がなぜ間違っているのか、多くの説明を聞いたり読んだりしてきました。多くの説明で高度な数学を何ページにもわたって用いていますが、私はそれは不要だと思います。これは単純な問いであり、単純な答えが求められます。そこで、私はこの問題に挑戦してみようと思います。
片方の封筒にもう片方の封筒の2倍の金額が入っているという事実をどう扱うか、非常に慎重に考える必要があります。小さい方の封筒の金額をS、大きい方の封筒の金額をLとしましょう。すると、次のようになります。
L=2×S
S=0.5×L
2つの要素と0.5の要素が異なる封筒に適用されていることに注目してください。両方の要素を同じ金額に適用することはできません。最初の封筒に100ドルが入っていた場合、小さい方の封筒であれば、もう1つの封筒には200ドルが入っています。100ドルが大きい方の封筒であれば、もう1つの封筒には50ドルが入っています。つまり、もう1つの封筒には50ドルか200ドルが入っています。しかし、そこからそれぞれの確率が50/50であると結論付けることはできません。なぜなら、0.5と2の要素を同じ金額に適用することになり、それは不可能だからです。そもそも賞金の配分がわからなければ、2つ目の封筒にいくら入っているかを推測することはできません。
0.5倍/2倍の議論が間違っている場合、もう一方の封筒の期待値を設定する正しい方法は何でしょうか? 私なら、2つの封筒の差額はLS = 2S-S = Sとします。封筒を切り替えると、Sが何であれ、利益を得るか損失を得ます。2つの封筒に50ドルと100ドルが入っている場合、切り替えると50ドルの利益または損失が発生します。2つの封筒に100ドルと200ドルが入っている場合、切り替えると100ドルの利益または損失が発生します。いずれにしても、切り替えによる期待利益は0です。最初の封筒に100ドルが入っている場合、もう一方の封筒の差額が50ドルになる確率と100ドルになる確率がそれぞれ50%あると言えると思います。したがって、期待利益は75ドルです。したがって、もう一方の封筒の期待値は、0.5×($100+$75) + 0.5×($100-$75) = 0.5×($175+$25) = $100 となります。
少しでも意味が伝われば幸いです。この問題はいつもたくさんのコメントをいただきます。もし何かご意見がありましたら、直接私にメールを送るのではなく、私のWizard of Vegasフォーラムに投稿してください。リンクは下記です。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
リンク
A、B、Cの3人が女性をめぐって死闘を繰り広げるトゥルエル(三者決闘)を考えてみましょう。彼らは全員紳士であり、以下のルールに同意しています。
- 3 人の参加者は三角形を形成します。
- それぞれ弾丸は1つだけです。
- 最初にA、次にB、そしてCが続きます。
- A が意図したターゲットに命中する確率は 10% です。
- B が意図したターゲットに命中する確率は 60% です。
- C が意図したターゲットに命中する確率は 90% です。
- 偶発的な発砲はありません。
- 空中での射撃(故意のミス)および自分自身の射撃は許可されており、常に成功します。
- どのラウンドでも2、3人の生存者が残っている場合、それぞれに新しい弾丸が与えられます。その後、同じ順番で交代で射撃を繰り返し、既に死亡した者を飛ばします。
- 参加者 3 人は全員完璧な論理学者です。
Aは最初に誰を狙うべきでしょうか?それぞれの初期ターゲットに対する彼の生存確率はどれくらいでしょうか?
このパズルはBBCの番組「Quite Interesting」で取り上げられています。答えと解答は100行下までスクロールしてください。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
それぞれの初期目標に応じて、Aが勝利する確率を以下に示します。ご覧のとおり、Aの勝利確率は意図的に空中に向けて発砲することで最大化されます。
トゥルーエルオッズ
| 戦略 | おそらく勝利 |
| 空気 | 13.887% |
| あ | 0.000% |
| B | 12.560% |
| C | 13.094% |
解答として、あるラウンドの後にグループXだけが残る確率をPr(X)と表記します。また、誰かが攻撃を受けてゲームの状態が変化するまで繰り返した後、グループXが最終的にラウンドに勝利する確率をPr(X*)と表記します。プレイヤーXが唯一の生存者となる確率をPr(X**)とします。最終的な確率を求めるために、まず2人のプレイヤーの状態を見てみましょう。それぞれが相手を撃つことは明らかです。
A対B
- Pr(A) = 0.1
- Pr(B) = 0.9×0.6 = 0.54
- Pr(AB) = 0.9×0.4 = 0.36
両者とも生き残った場合、生き残りが1人になるまでこの繰り返しが行われます。つまり、最後の生き残りとなる確率は以下のとおりです。
- Pr(A*) = Pr(A)/(1-Pr(AB)) = 0.1/0.64 = 0.15625
- Pr(B*) = Pr(B)/(1-Pr(AB)) = 0.54/0.64 = 0.84375
A対C
- Pr(A) = 0.1
- Pr(C) = 0.9×0.9 = 0.81
- Pr(AC) = 0.9×0.1 = 0.09
両者とも生き残った場合、生き残りが1人になるまでこの繰り返しが行われます。つまり、最後の生き残りとなる確率は以下のとおりです。
- Pr(A*) = Pr(A)/(1-Pr(AC)) = 0.1/0.91 = 0.10989011
- Pr(C*) = Pr(B)/(1-Pr(AC)) = 0.81/0.91= 0.89010989
B対C
- Pr(B) = 0.6
- Pr(C) = 0.4×0.9 = 0.36
- Pr(BC) = 0.$×0.1 = 0.04
両者とも生き残った場合、生き残りが1人になるまでこの繰り返しが行われます。つまり、最後の生き残りとなる確率は以下のとおりです。
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0.6/.96 = 0.625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0.36/.96= 0.375
3人プレイの場合を分析する準備ができました。AがBを狙っている状況を考えてみましょう。
3人プレイ — AがBを狙う
AがBを攻撃した場合、Cは確実に生き残りますが、Aを攻撃するかどうかはわかりません。つまり、Bを攻撃した場合の2つの可能な結果はACとCです。AがBを攻撃しなかった場合、Bはより脅威となるCを狙います。BがCを攻撃した場合、AとBは生き残ります。BがCを攻撃しなかった場合、Cはより脅威となるBを狙います。CがBを攻撃しなかった場合、3人とも生き残ります。CがBを攻撃した場合、AとCは生き残ります。つまり、可能な結果はC、AB、AC、ABCです。
- Pr(A) = 0です。
- Pr(B) = 0です。
- Pr(C) = 0.1 × 0.9 = 0.09。これは、AがBに衝突し、次にCがAに衝突することで達成されます。
- Pr(AB) = 0.9 × 0.6 = 0.54。これは、AがBをミスし、その後BがCをヒットすることで達成されます。
- Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334。これは2つの方法で達成できます。1つ目は、AがBに当たり、その後CがAをミスすることです。2つ目は、AがBをミスし、BがCをミスし、その後CがBに当たることです。
- Pr(BC) = 0です。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。これは3つすべてが欠けている状態で達成されます。
2 人のプレイヤーの場合と同じ論理で、ラウンド後にゲームの状態が変化したと仮定して、各結果を (1-Pr(ABC))=0.964 で割って、各状態の確率を見つけることができます。
- Pr(C*) = 0.09/0.964 = 0.093361。
- Pr(AB*) = 0.54/0.964 = 0.560166。
- Pr(AC*) = 0.334/0.964 = 0.346473。
2人プレイの場合、AとBの2人プレイではAが0.15625の確率で勝ち、Bが0.84375の確率で勝つことがわかります。AとCの2人プレイではAが0.109890の確率で勝ち、Cが0.890110の確率で勝つことになります。
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600。Aが勝者になるには2つの方法があります。(1) AB状態に到達してから勝利する、または(2) AC状態に到達してから勝利する。
- Pr(B**) = 0.560166 × 0.84375 = 0.472640。BがAB状態に到達し、その後Bが勝利すればBが勝者となる。
- Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760。Cが勝つには、AがBを倒し、その後Cが第1ラウンドでAを倒すか、または状態ACに到達し、その後Cが勝利する必要があります。
したがって、A の戦略が最初に B を狙うことである場合、彼が唯一生き残る確率は 12.56% です。
3人プレイ — AがCを狙う
AがCを攻撃した場合、Bは確実に生き残りますが、Aを攻撃するかどうかはわかりません。つまり、Cを攻撃した場合の2つの可能な結果はABとBです。AがCを外した場合、Bはより脅威となるCを狙います。BがCを攻撃した場合、AとBは生き残ります。BがCを外した場合、Cはより脅威となるBを狙います。CがBを外した場合、3つすべてが生き残ります。CがBを攻撃した場合、AとCは生き残ります。つまり、可能な結果はB、AB、AC、ABCです。
- Pr(A) = 0です。
- Pr(B) = 0.1 × 0.6 = 0.06です。
- Pr(C) = 0です。
- Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04 + 0.54 = 0.58。これは2つの方法で実現できます。1 つ目は、A が C にヒットし、その後 B が A をミスした場合です。2 つ目は、A が B をミスし、その後 B が C にヒットした場合です。
- Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324。これは、AがCをミスし、BがCをミスし、CがBにヒットすることで達成されます。
- Pr(BC) = 0です。
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036。これは3つすべてが欠けている状態で達成されます。
2 人のプレイヤーの場合と同じ論理で、ラウンド後にゲームの状態が変化したと仮定して、各結果を (1-Pr(ABC))=0.964 で割って、各状態の確率を見つけることができます。
- Pr(B*) = 0.06/0.964 = 0.062241。
- Pr(AB*) = 0.58/0.964 = 0.601660。
- Pr(AC*) = 0.324/0.964 = 0.336100。
A が B を目的とするケースの解決策と同じ論理により、
- Pr(A**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943。
- Pr(B**) = 0.062241 + 0.601660 × 0.84375 = 0.569891。
- Pr(C**) = 0.336100 × 0.890110 = 0.299166。
したがって、A の戦略が最初に C を狙うことである場合、彼が唯一生き残る確率は 13.09% です。
3人プレーヤー — Aが故意にミス
Aが故意にミスをした後、Bはより大きな脅威であるCを狙います。BがCを命中させれば、AとBは生き残ります。BがCをミスした場合、Cはより大きな脅威であるBを狙います。CがBをミスした場合、3人とも生き残ります。CがBを命中させれば、AとCは生き残ります。つまり、起こり得る結果はAB、AC、ABCです。
- Pr(A) = 0です。
- Pr(B) = 0です。
- Pr(C) = 0です。
- Pr(AB) = 0.6。これはBがCを打つことで達成される。
- Pr(AC) = 0.4 × 0.9 = 0.36。これは、BがCをミスし、その後CがBをヒットすることで達成されます。
- Pr(BC) = 0です。
- Pr(ABC) = 0.4 × 0.1 = 0.04。これは3つすべてが欠けている状態で達成されます。
2 人のプレイヤーの場合と同じ論理で、ラウンド後にゲームの状態が変化したと仮定して、各結果を (1-Pr(ABC))=0.96 で割って、各状態の確率を見つけることができます。
- Pr(AB*) = 0.6/0.96 = 0.625です。
- Pr(AC*) = 0.36/0.96 = 0.375。
A が B を目的とするケースの解決策と同じ論理により、
- Pr(A**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865。
- Pr(B**) = 0.625 × 0.84375 = 0.527344。
- Pr(C**) = 0.375 × 0.890110 = 0.333791。
したがって、A の戦略が最初に C を狙うことである場合、彼が唯一生き残る確率は 13.89% です。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
一度に 2 つの要素を比較し、比較の最大数を最小限に抑えながらリストを並べ替える最も速い方法は何ですか?
同等に優れた方法はいくつかありますが、私が最も理解しやすいと思うのはマージソートと呼ばれる方法です。その仕組みは以下のとおりです。
- リストを2つに分割します。各サブセットのサイズが1または2になるまで、各サブセットを2つに分割し続けます。
- 2 の各サブセットを、小さい方の要素を先頭にして並べ替えます。
- サブセットのペアを結合します。ソートされたリストが1つになるまで繰り返します。
2つのリストをマージする方法は、各リストの最初のメンバーを比較し、小さい方を新しいリストに追加します。これを繰り返し、小さい方を前回の比較で比較した小さい方の後ろに追加します。2つのグループが1つのソートされたグループに結合されるまで、これを繰り返します。元の2つのリストのどちらかが空の場合は、もう一方のリストをマージ後のリストの末尾に追加できます。
次の表は、リスト内の要素数に応じて必要な比較の最大数を示しています。
マージソート
| 要素 | 最大比較 |
| 1 | 0 |
| 2 | 1 |
| 4 | 5 |
| 8 | 17 |
| 16 | 49 |
| 32 | 129 |
| 64 | 321 |
| 128 | 769 |
| 256 | 1,793 |
| 512 | 4,097 |
| 1,024 | 9,217 |
| 2,048 | 20,481 |
| 4,096 | 45,057 |
| 8,192 | 98,305 |
| 16,384 | 212,993 |
| 32,768 | 458,753 |
| 65,536 | 983,041 |
| 131,072 | 2,097,153 |
| 262,144 | 4,456,449 |
| 524,288 | 9,437,185 |
| 1,048,576 | 19,922,945 |
| 2,097,152 | 41,943,041 |
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
2010年10月29日、 ラスベガス・レビュー・ジャーナル紙はリード対アングル上院議員選挙の世論調査を掲載しました。625人の有権者を対象とした調査では、アングル氏が49%、リード氏が45%の支持を得て勝利しました。また、誤差は4%とされています。そこで、私の疑問点は以下のとおりです。
- アングルが勝つ確率はどれくらいでしょうか?
- アングル氏の得票率の 95% 信頼区間はどれくらいでしょうか?
- 誤差の範囲とは何を意味しますか?
少し古い返信で申し訳ありません。選挙前に以下の記事を書きました。
まず、残りの6%を除外します。彼らはまだ決めていないか、第三政党の候補者、あるいはネバダ州では選択肢となる「どちらでもない」に投票するでしょう。この仮定に異論を唱える人もいるかもしれません。正直なところ、彼らを無視するもう一つの理由は、候補者が2人以上になると計算が複雑になるからです。つまり、四捨五入すると、アングル氏に306票、リード氏に281票、合計587票がサンプルに残ります。
この質問に答えるために、標準正規分布の近似値を用います。もし完璧主義者なら、実際の平均値と分散が不明なため、 T分布を使用します。しかし、私の意見では、正規分布の場合、標本サイズは587で十分です。
サンプルサイズ = 306+281 = 587。
角度サンプル平均は 306/587 = 0.521295 です。
平均値の推定標準偏差は(0.521295 × 0.478705 / (587-1))^0.5 = 0.0206361です。
50%を超えるAngleのシェアは、(0.521295-0.5)/0.0206361 = 1.031917標準偏差です。
正規分布によれば、リードが期待値より1.031917標準偏差高い成績を残す確率は0.151055です。これはExcelの関数NORMSDIST(-1.031917)で計算できます。したがって、アングルの勝利確率は1-0.151268 = 84.89%となります。
95%信頼区間を作成するには、ガウス曲線の両側2.5%の点が平均値から1.959964標準偏差離れていることに留意してください。これはExcel関数NORMSINV(0.975)で求めることができます。既に述べたように、標本平均値の推定標準偏差は0.0206361です。したがって、どちらの候補者も世論調査結果から0.0206361×1.959964 = 0.040446標準偏差以内に収まる確率は95%です。したがって、Angleの95%信頼区間は0.521295 +/- 0.040446 = 48.08%から56.17%となります。
「アングル/リード選挙におけるアングルの得票数のうち、アングルの得票数が48.08%と56.17%の間に収まる確率は95%である」と表現するのは数学的に正しくないと言われました。当初はそう表現したのですが、二人の統計学者が私の表現に愕然としました。彼らの返答を言い換えると、「48.08%と56.17%がアングルの得票数を95%の確率で取り囲む」と受動態で表現しなければならないと言われました。正直に言うと、私には同じに聞こえます。しかし、彼らは信頼区間はランダムでアングルの得票数は不変であり、私の最初の表現は正反対の意味を示唆していると強調しました。いずれにせよ、頻度主義の統計学者の方々には、後者の表現で納得していただければ幸いです。
「誤差幅」とは、95%信頼区間の両端の差の半分です。この場合、(56.17% - 48.08%)/2 = 4.04%となります。
続いて、実際の結果は次のとおりです。
リード:361,655
角度: 320,996
その他: 21,979
つまり、「その他」の票を除くと、リード氏は53.0%、アングル氏は47.0%を獲得した。リード氏が6%の差で快勝したことになる。では、なぜ世論調査がこれほど大きく外れたのかという疑問が湧いてくる。偶然だったのだろうか?有権者の考えが変わったのだろうか?それとも、そもそも世論調査が悪かったのだろうか?これらの疑問は読者の皆さんに委ねます(教科書にそう書いてあるのが嫌なのです)。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
保険数理計算ツールを試してみました。私の予想死亡年齢に達する確率が50%未満なのはなぜですか?
平均値と中央値を混同していますね。私の状況を例に考えてみましょう。私は45歳の男性です。平均寿命は78.11歳ですが、80歳まで生きる確率は50.04%です。
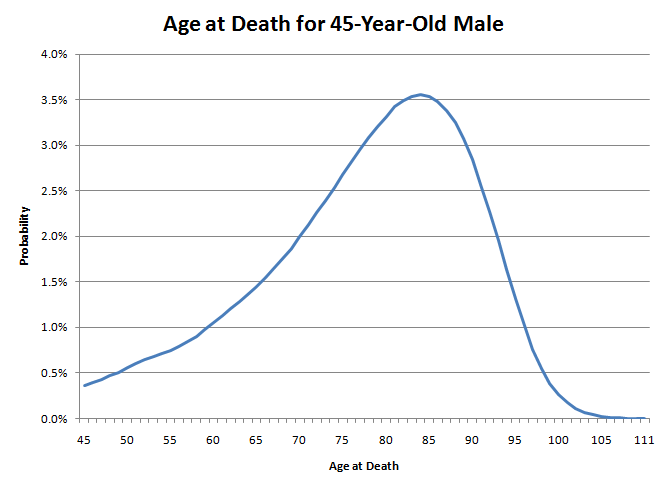
私が死ぬ年齢は、このグラフにダーツを投げるようなものです。左の裾が右よりもずっと太いことに注目してください。これは、現時点での私の死亡確率が非常に低いことを意味します。しかし、年齢を重ねるにつれて、来年の死亡確率は高くなっていきます。たとえば、45歳の男性の場合、46歳まで生き残る確率は99.64%とかなり高くなります。しかし、85歳になると、86歳まで生きられる確率はわずか89.21%になります。これは、自然が背中にゆっくりとナイフを突き刺すようなものです。最初はおそらく死なないでしょうが、年を経るごとに、死ぬ確率はゆっくりと高まります。しかし、70代後半になると、自然はもういい加減にして、本当にナイフを押し込み始めます。
つまり、45歳の男性が多数このグラフにダーツを投げた場合、49.96%が45歳から79歳の間に、50.04%が80歳から111歳の間にダーツを投げることになります。しかし、グラフの右側にたどり着く幸運な半分の男性は、おそらく80歳を超えて長く生きることはないでしょう。男性は80歳に達すると、あと7.78年しか生きられないと予想されます。一方、80歳まで生きられない不運な半分の多くは、それよりもはるかに若くして亡くなります。つまり、平均寿命を縮めているのは、若死が多いことです。
同様の状況として、10、20、30、31、32、33 の番号がついたサイコロを考えてみましょう。平均は 26 ですが、それ以上の目が出る可能性は 2/3 あります。
平均値と中央値の違いを示す例として、サンプルにさらに2人の死亡者を追加したとします。1人は46歳、もう1人は81歳です。80歳まで生きる確率は変わりませんが、45歳時点での平均寿命は短くなります。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
伸ばされていない状態で1kmの長さの、無限に伸縮するゴムバンドを想像してみてください。ゴムバンドは毎秒1kmの速度で伸びます。次に、ゴムバンドの片方の端にアリがいると想像してください。ゴムバンドが伸び始めると、アリは現在の位置から毎秒1cmの速度で反対側の端に向かって移動します。アリは反対側の端にたどり着くことができるでしょうか?もしできるとしたら、それはいつでしょうか?
はい、e 100,000 -1 秒後には解けます。mathproblems.infoの問題 206 に 2 つの解答がありますので、そちらをご覧ください。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
燃費向上はハイブリッド車の追加費用に見合う価値があると思いますか? 元を取るにはどれくらいの距離を走行する必要がありますか?
いい質問ですね。それに答えるために、購入を検討しているトヨタ・ハイランダーを検討しました。標準のハイブリッドモデルの小売価格は37,490ドルです。同じ四輪駆動車で非ハイブリッドモデルの価格は29,995ドルです。つまり、ハイブリッドエンジン搭載車は価格に7,495ドル上乗せされることになります。
ハイブリッド車の燃費は、市街地と高速道路の両方で時速28マイル(約45km/h)です。非ハイブリッド車の燃費は、市街地で時速17マイル(約17km/h)、高速道路で時速22マイル(約22km/h)です。平均燃費は時速19.5マイル(約19.5km/h)としましょう。
損益分岐点に達するマイル数の一般的な公式は、h×m h ×m r /(g×(m h -m r ))です。
h = ハイブリッドの追加コスト。
g = ガソリン1ガロンあたりのコスト。
m r = 非ハイブリッド車の走行距離(「r」は普通車の場合)。
m h = ハイブリッド車の燃費。
次の表では、この式を使用して、1 ガロンあたり 2 ドルから 5 ドルまでのさまざまなガソリン価格の損益分岐点を計算しています。
ハイブリッド損益分岐点
| ガソリン代 | マイル数 |
| 2.00ドル | 240,722 |
| 2.25ドル | 213,975 |
| 2.50ドル | 192,577 |
| 2.75ドル | 175,070 |
| 3.00ドル | 160,481 |
| 3.25ドル | 148,136 |
| 3.50ドル | 137,555 |
| 3.75ドル | 128,385 |
| 4.00ドル | 120,361 | 4.25ドル | 113,281 |
| 4.50ドル | 106,987 |
| 4.75ドル | 101,357 |
| 5.00ドル | 96,289 |
つまり、ラスベガスの現在のガソリン価格(1ガロンあたり3ドル)を考えると、ハイブリッド車が有利になるには160,481マイル(約26万480キロ)以上走行する必要があるということです。これは、ハイブリッド車に付随する高額なバッテリー交換費用や、化石燃料の消費量が少ないことで得られるグリーンポイントなど、その他の費用を考慮していません。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
一卵性双生児以外の兄弟姉妹と共通する遺伝子の比率はどのくらいでしょうか?
1/2。
キノに例えると、誰もが40個の遺伝子を持ち、それぞれがキノのボールで表現されます。ただし、それぞれのボールには固有の番号が振られています。血縁関係のない二人が交配すると、それは二人で80個のボールをホッパーに集め、交配によって生まれた子孫のために40個の遺伝子をランダムに選択するようなものです。
つまり、あなたが受胎した時、あなたはホッパーに入っていたボールの半分を受け取り、残りの半分は無駄になりました。あなたの兄弟姉妹が受胎した時、彼または彼女はあなたが生まれた時に抽選されたボールの半分を受け取り、残りの半分は抽選されなかったボールを受け取りました。つまり、あなたは遺伝的に50%同一です。これは、キノで40個の数字が抽選された場合、2回連続して抽選されると平均20個のボールが共通するのと同じ理由です。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
テーブルと椅子を生産する工場には、のこぎり10台、旋盤6台、研磨機18台が備え付けられています。椅子1脚の製作には、のこぎりで10分、旋盤で5分、研磨で5分かかります。テーブル1脚の製作には、のこぎりで5分、旋盤で5分、研磨で20分かかります。椅子の販売価格は10ドル、テーブルの販売価格は20ドルです。工場が1時間あたりにテーブルと椅子を何脚生産すれば、最大の収益が得られるでしょうか?また、その収益はいくらでしょうか?
1時間あたりに製造される椅子の数をc、テーブルの数をtとすると、1時間あたりの収益は10×c + 20×tとなります。
10台ののこぎりで1時間あたり600分の鋸引き作業が必要になります。椅子の場合は鋸引きに10分、テーブルの場合は5分かかると仮定すると、1時間あたりの生産量は以下のようになります。
(1)10セント+5トン<=600
旋盤6台で1時間あたり360分の旋盤加工が可能です。椅子は鋸で5分、テーブルは5分かかると仮定すると、1時間あたりの生産量は以下のようになります。
(2)5c + 5t <= 360
18台のサンディングマシンで1時間あたり1080分のサンディング作業が行われます。椅子の場合は鋸で5分、テーブルの場合は20分かかると仮定すると、1時間あたりの生産量は以下のようになります。
(3)5c + 20t <= 1080
次のグラフは、3組の機械によって課される3つの制約を示しています。工場は、3本の線すべてに該当する椅子とテーブルの組み合わせを自由に生産できます。問題は、3本の線のうちどの線に該当する場合、収益が最大になるかということです。
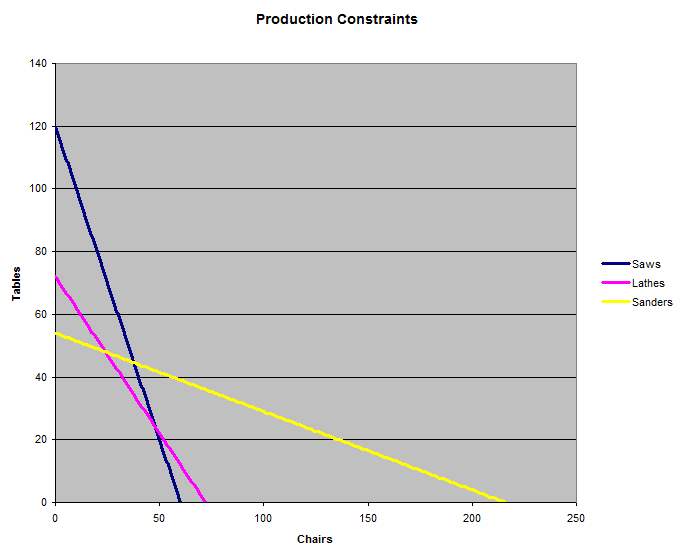
答えは当然、2本の直線の交点、椅子を全て作るか、テーブルを全て作るかのいずれかになるでしょう。では、直線が交差する場所を見つけましょう。まず、式(1)と(2)が交差する場所を見つけましょう。機械の能力を最大限に引き出すために、<= という式を = に置き換えることができます。
(1)10セント+5トン=600
(2)5c + 5t = 360
(1)から(2)を引く:
5セント = 240
c = 48
式(1)にcの48を代入すると、
10×48 + 5t = 600
5t = 120
t = 24
したがって、式(1)と式(2)は椅子48脚とテーブル24台のところで成り立ちます。
次に、式(2)と式(3)が交わる場所を見つけましょう。
(2)5c + 5t = 360
(3)5セント+20トン=1080
(3)から(2)を引くと、
15トン = 720
t = 48
これを(2)または(3)に代入するとcを解くことができ、それは24です。
したがって、式(2)と式(3)は椅子24脚とテーブル48台のところで成り立ちます。
グラフから鋸とサンダーの線が交わるところが旋盤の制約の外側にあることがわかるので、方程式(1)と(3)が交わるところを探す必要はありません。
椅子だけを作るのが正解である可能性もあります。グラフからわかるように、椅子だけを作る場合、鋸が最大の制約となります。式(1)から、テーブルの数を0とすると、c=60となります。
もう一つの可能性は、テーブルだけを作ることです。グラフから、サンダーが最大の制約となることがわかります。式(3)に椅子を0脚と代入すると、テーブルは54台しか作れないことがわかります。
次のグラフは、それぞれの有効な回答に対する総収益を示しています。収益は椅子1脚あたり10ドル、テーブル1台あたり20ドルです。
総時間収入
| 椅子 | テーブル | 収益 |
| 0 | 54 | 1,080ドル |
| 24 | 48 | 1,200ドル |
| 48 | 24 | 960ドル |
| 60 | 0 | 600ドル |
王様はワインがいっぱい入った樽を持っています。
月曜日の夜、召使いが樽からカップ3つを盗み、代わりに水3つを入れました。
火曜日の夜、別の召使いが薄まったワインの樽から3杯のワインを盗み、代わりに3杯の水を入れました。
水曜日の夜、また別の召使いが、薄まったワインの樽から3杯のワインを盗み、代わりに3杯の水を入れました。
木曜日の朝、樽にはワインが50%、水が50%入っています。
最初に樽の中に入っていたワインの量はどれくらいですか?
もし200個のスキットルズが入ったボウルがあって、そのうち3個を食べると死ぬとしたら、12個を一掴みして全部食べたら死ぬ確率はどれくらいでしょうか?毒入りのスキットルズ1個で死ぬと仮定しましょう。
宇宙人が10人の論理学者を誘拐し、ある部屋に閉じ込めました。宇宙人はまず、背の高い人から低い人の順に一列に並べ、各人が次に背の低い人の方を向くように指示します。こうすることで、各人は背の低い論理学者全員を見ることができますが、背の高い論理学者は見えなくなります。そして宇宙人は、各人に白か黒の帽子をかぶせると説明します。ただし、自分の帽子の色は見えず、背の低い論理学者の帽子しか見えません。白と黒の帽子の配置は、必ずしも5対5である必要はなく、自由に決められます。
エイリアンは、背の高い人から順番に、それぞれの論理学者に帽子の色を尋ねると説明します。論理学者たちは、自分より前に行動している人の答えを聞くことができます。ゲーム開始後は、白黒の答え以外、いかなるコミュニケーションも行ってはなりません。複数の論理学者が間違えた場合、全員が食べられてしまいます。9人以上が正解した場合、無事に地球に帰還します。エイリアンは彼らに戦略を練る時間を与えます。彼らの戦略は何でしょうか?
一つの戦略として、まず最初に行動する論理学者に、黒い帽子が偶数個見えたら「黒」、他の9人の論理学者が黒い帽子を奇数個見えたら「白」と言わせます。論理学者は自分の帽子の色と一致する確率が50%なので、間違えても構いません。論理学者が何を言ったとしても、それを「ランニングカラー」と定義します。
次に、2番目に行動する論理学者は、8人の短い論理学者の黒い帽子の数を数え、最初の論理学者と同じ奇数と偶数の方法で色を当てはめます。これが最初の論理学者が述べた色と一致する場合、彼は白い帽子を持っているはずなので、白と述べます。一致しない場合、彼は黒い帽子を持っているはずなので、黒と述べます。彼が「白」と答えた場合、現在の色は変わりません。彼が「黒」と答えた場合、現在の色は反対色に変わります。
次に、3番目に行動する論理学者は、2番目と全く同じ行動をとりますが、7人の短い論理学者の黒い帽子の数を数えます。同様に、彼が現在進行中の色に同意する場合は「白」と言い、進行中の色は変わりません。彼が現在進行中の色に同意しない場合は「黒」と言い、進行中の色が反転します。
他の論理学者も皆、まったく同じことを行うでしょう。
もちろん、黒を奇数、白を偶数と関連付けることも容易にできます。重要なのは、どの色がどの奇数/偶数パリティを意味するかについて、全員が同意していることです。どちらの戦略を採用しても、2番目から10番目に行動する論理学者は全員正解となり、最初に行動する論理学者は50%の確率で正解するため、全員が生き残ります。この戦略は、論理学者の人数に関係なく有効です。
アクセルとボブはそれぞれ52枚のカードのデッキを持っています。二人ともデッキをランダムにシャッフルします。そして、それぞれのデッキから同時に1枚ずつカードをめくります。二人が同じカードを少なくとも1回同時にめくる確率はどれくらいでしょうか?
答えを1-(51/52) 52 = 0.63568648と簡単に推定できます。しかし、推定だけでは知識として納得できません。では、正確な解を求めましょう!
ステップ 1: まず、最初のカードが 1 番である場合に 2 番目のデッキを並べる方法の数を考えます。答えは、他の 51 枚のカードを並べる方法の数で、51! = 15511187532873822802242430164693032110632597200169861120000000000000 です。
どのカードも最初のデッキと一致する可能性があるため、52枚すべてに対してこの手順を実行する必要があります。これにより、少なくとも1枚のカードが一致する組み合わせは52*51! = 52!通りになります。
ステップ2:ただし、ステップ1では、2枚のカードが一致するすべての状況を2倍にカウントします。例えば、最初の2枚のカードが1と2の場合、他のカードの配置方法は50!通りで、1枚目を最初のカードとして1回、2枚目を2枚目として2回、計2回カウントします。52枚の中から2枚のカードを選ぶ方法はcombin(52,2) = 1326通りです。2枚のカードの組み合わせごとに、他のカードを並べる方法は50! = 30414093201713378043612608166064768844377641568960512000000000000通りあります。したがって、ステップ2では、combin(52,2)*50! = (52*51/2!)*50! = 52!/2!通りの組み合わせを減算する必要があります。
ステップ 3: 次に、ランダム デッキの最初の 3 枚のカードが 1、2、3 の順に並んでいる状況を考えます。残りの 49 枚のカードを並べる方法は 49! 通りあります。少なくとも 1 枚の一致するカードを数える最初のステップで、それらを 3 回数えたことになります。次に、2 番目のステップで、これらの 3 枚のカードから 2 枚を選ぶ combin(3,2)=3 通りの方法をすべて差し引きます。つまり、この状況は 3-3=0 回数えられたことになるので、それらを再び追加する必要があります。少なくとも 3 枚の一致するカードを選ぶ状況は combin(52,3) 回あります。したがって、combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! 通りの組み合わせを再び追加する必要があります。
ステップ 4: 次に、ランダム デッキの最初の 4 枚のカードが 1、2、3、4 の順に並んでいる状況を考えます。残りの 48 枚のカードを並べる順序は 48! 通りあります。少なくとも 1 枚の一致するカードを数える最初のステップで、それらを 4 回数えます。次に、ステップ 2 でこれらの 4 枚のカードから 2 枚を選ぶ combin(4,2)=6 通りをすべて差し引きます。次に、これらの 4 枚のカードから 3 枚を選ぶ combin(4,3)=4 通りをすべて加算します。つまり、このような状況はそれぞれ 4-6+4=2 通り数えられます。したがって、これらの方法の 1 つを差し引いて、各状況が 1 回ずつ数えられるようにする必要があります。このような状況は、combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! 通りあります。
これを繰り返して、加算と減算を交互に繰り返し、重複カウントを修正します。
最終的に、ランダム デッキ内の少なくとも 1 枚のカードが順序付けられたデッキと一致する状況の数 = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783。
52 枚のカードを並べる方法は全部で 52! = y = 527177615496365219422618541545122659969212453861982208000000000000 通りあります。
したがって答えはx/y = 0.6321205588285576784044762298となる。
一致するものがない確率は、1-(x/y) = 0.3678794411714423215955237702 です。
この数字に見覚えがあるなら、その通りです。1/e = 0.3678794411714423215955237702。
したがって、答えは 1-(1/e) と非常に近い値と推定できます。
謝辞
数学的計算はPari/GPで行われた。
この問題は、Wizard of Vegasの私のフォーラムで質問され、議論されました。
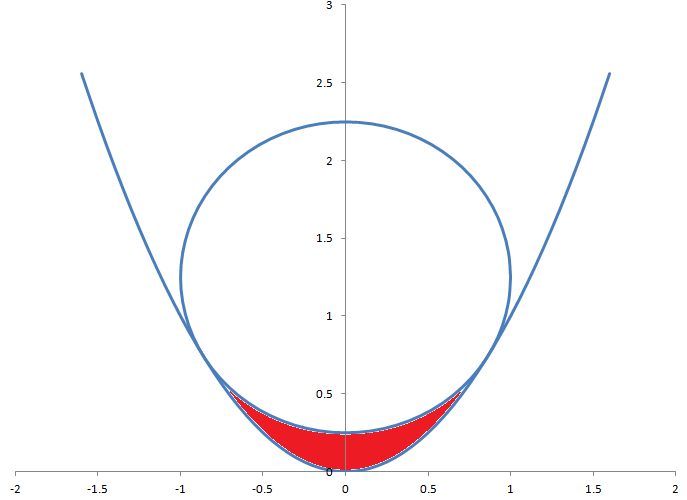
半径1の円は、方程式y=x 2の放物線に接しています。円と放物線の間の赤い領域の面積はいくらですか?
答えについては下のボタンをクリックしてください。
これが私の解決策です。(PDF)
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
この問題は、Mind Your Decisionsの Presh Talwalker さんから知りました。
カジノディーラーが新しいスリーカードポーカーのバリエーションに取り組んでいます。彼女は標準デッキからすべての絵札を取り、よくシャッフルします。そして、プレイヤー1に3枚、プレイヤー2に3枚、プレイヤー3に3枚、そして最後の3枚をプレイヤー4に配ります。4つのハンド全てにストレート(どのスートのJQK)が含まれる確率はどれくらいでしょうか?

最初のハンドが AKQ である確率は、1*(8/11)*(4/10) = 29.09% です。
最初の手札がすでに AKQ である場合、2 番目の手札が AKQ である確率は、1*(6/8)*(3/7) = 32.14% になります。
1回目と2回目がすでにAKQである場合、3回目の手がAKQである確率は1*(4/5)*(2/4) = 40.00%となる。
最初の3つのハンドがAKQであることを考えると、残りのカードは必ずAKQである必要があります。したがって、確率は上記の3つの確率の積、つまり216/5775 = 約0.037402597となります。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
半径 1 の円にランダムに内接する長方形の平均面積と周囲の長さはどれくらいですか?
いい質問ですね。私の答えは次のとおりです。
両方の問題に対する私の解決策は次のとおりです (PDF)。
次の 10 桁の数字を見つけます。
- 数字の最初の桁は、数字全体に含まれる 0 の数です。
- 数字の 2 番目の桁は、数字全体に含まれる 1 の数です。
- 数字の 3 番目の桁は、数字全体に含まれる 2 の数です。
- 数字の 4 桁目は、数字全体のうちの 3 の数です。
- 数字の 5 桁目は、数字全体のうちの 4 の数です。
- 数字の6桁目は、数字全体のうちの5の数です。
- 数字の 7 桁目は、数字全体のうちの 6 の数です。
- 数字の 8 桁目は、数字全体のうちの 7 の数です。
- 数字の 9 桁目は、数字全体のうちの 8 の数です。
- 数字の 10 番目の桁は、数字全体における 9 の数です。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
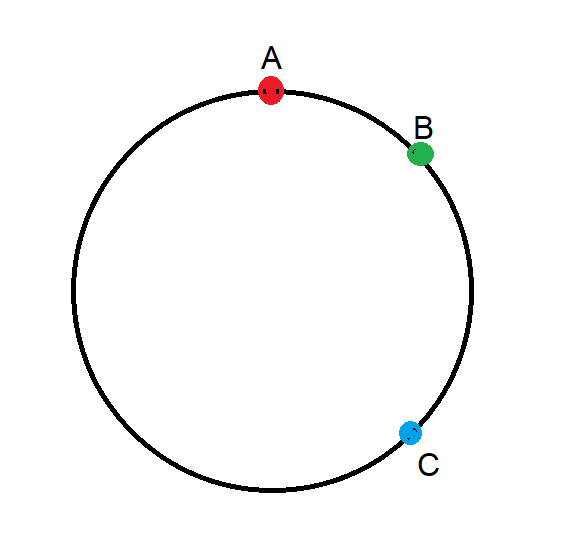
半径 1 の円に沿って 3 つの点がランダムかつ均一に分布しています。円周に沿って距離を測定する場合、3 つの点間の予想される最小距離はどれくらいでしょうか。
アリスとビルが家を塗装するのに3時間かかります。
アリスとシンディが家を塗装するのに4時間かかります。
ビルとシンディが家を塗装するのに5時間かかります。
全員で塗装するとどれくらい時間がかかりますか?
これが私の解決策です(PDF)。


