Wizardに尋ねる #163
ウィザードさん、バロナ・バレー・ランチで現在試験運用中の新しい「サーバーベース」スロットマシンについてどう思いますか？どうやらこの技術のおかげで、カジノはバックオフィスから瞬時にマシンの設定を変更できるそうです。ゲームの種類、額面、そして…配当まで！これはちょっとやりすぎだと思います。カジノ側が特定のプレイヤー（例えば酔っ払ったハイローラー）をターゲットにして、そのプレイヤーが勝ちにくくするのをどうやって防げるというのでしょう？カジノがいつでもどんなプレイヤーでも監視できることは周知の事実です。監視とこの技術の組み合わせは、カジノ側にあまりにも大きな優位性を与えているように思えます。テーブルプレイヤーがディーラーやピットボスとハンドのことで激しく口論になったとします（たまに起こります）。その同じプレイヤーがスロットマシンに行けば、カジノ側は仕返しに彼のマシンの配当を下げることができるのでしょうか？もちろん、特定のプレイヤーを「優遇」することもでき…それも同じように危険です。ゲームや額面の変更を許可することには大賛成ですが、配当率に関しては規制当局が関与すべきではないでしょうか???
聞いたところによると、マシンで設定できるものはすべてサーバー経由でリモート設定できるそうです。これには理論上の還元率も含まれます。しかし、ほとんどのカジノでは、スロットマシンの理論上の還元率を変更するには多くの書類手続きが必要だと報告しています。
たとえスロットマシンのリターンレバーを上下に動かすのが楽だったとしても、カジノがプレイヤー一人ひとりにそうすると考えるのは陰謀論のように思えます。ここラスベガスに住んでいると、カジノが勝つためにどんなことをするのか、酸素を送り込んだり、「負ける負ける負ける」という亜音速の呪文を唱えたりといった、様々な説を耳にします。これらは単なる都市伝説です。ほとんどのカジノは、プレイヤーに良い体験と公平なギャンブルを提供すれば、彼らはまた戻ってくると正しく信じています。諺にもあるように、「羊は一度しか屠殺できないが、毛刈りは何度でもできる」のです。（ベジタリアンである私のウェブマスター、マイケル・ブルージェイは、代わりにこんな例え話をするように勧めてきました。「羊のお金を全部奪うのは一度だけだが、羊に何度もボウリングに連れて行かせることはできる」。）
アイオワ州中部のメスカキでは、スペイン 21 でエースを分割すると、エースには 3 対 2、エースを分割すると 10 が支払われます。このルールの影響は何ですか?
これにより、ハウスエッジが 0.16% 低下します。
あなたは淡水湖で、岩を載せたボートに乗っています。岩を湖に投げ入れます。陸地（岸）を基準にすると、水位は上昇しますか、下降しますか、それとも一定のままですか？同僚たちは水位は一定のままだと考えています。
岸に対する水位は低下します。ボートの中では、岩がカヌーを押し下げ、周囲の水を押し上げています。押しのけられる水の量は、岩の重さと等しくなります。例えば、10ポンドの岩は、10ポンドの水を上方に押し上げます。岩を船外に投げ出す場合、重さではなく、岩の体積が重要になります。つまり、岩は岩と同じ体積の水を押し上げます。岩の質量は水の質量よりも大きいため、岩は岩の中にある水よりも、岩を押し下げる水のほうが多く押しのけます。そのため、湖の水位は、岩がカヌーの中にある場合の方が、湖底にある場合よりも高くなります。
インターネットギャンブルを統括する団体を探し回ってきましたが、本当にあるのでしょうか？
簡単に答えると、いいえ。
こんにちは。まずは素晴らしいサイトを開設されたことをお祝い申し上げます。本当に興味深いですね。デュース・ワイルドにおける「最適な」戦略について質問があります。このゲームの付録では、捨てるカードの種類に応じて、同じスーツのカードを2枚キープするか、すべて捨てるかを選ぶと書かれています。付録1の例では、手札は次のようになっています。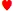
、、
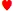、この場合、すべて捨てるべきです。もし同じハンドで、最後のカードが（7dではなく）8dだった場合、同じスーテッドのKhとQhは残すべきです。質問なのですが、捨てるカード（3c、4d、7）によって何が変わるのでしょうか？または3c,4 、8 ）ロイヤルフラッシュ（あるいはストレートフラッシュ、あるいは他のどんなカードでも）が出る確率は、私には同じに思えます。ロイヤルフラッシュに必要なカードが既に2枚あるのなら、捨てるカードが何であれ、それを取っておいた方がいいのではないでしょうか？
ありがとうございます。ペナルティカードに関する質問には以前にも回答しましたが、重要な概念なのでもう一度お答えします。キングとクイーンをどちらの手札に残す期待値は同じというのはその通りです。しかし、7dでは8dよりも全てを捨てる価値が少し高くなります。正確に言うと、7で全てを捨てるとストレートを作る方法は1,606通りありますが、8dの場合は1,591通りしかありません。捨て札が離れているほど、ドローでストレートを作るのは難しくなります。このケースは非常にギリギリです。7を捨てることでストレートを作る15通りの方法は、ロイヤルのために2枚を残すよりも、すべてを捨てる方が価値が高くなります。同じ理由で、6デッキのブラックジャックでは、A2は5に対してはダブルしますが、4にはダブルしません。どちらの場合もダブルの価値は同じですが、4に対してはヒットする方が価値が高く、ダブルの価値を上回ります。
カードの除去とディーラーのアップカードとを混同されているようです。以下の表は、ディーラーがブラックジャックを確認する前の、ディーラーがソフト17とインフィニットデッキでスタンドした場合の、ディーラーのアップカードのみに基づくプレイヤーの期待値を示しています。
ディーラーのアップカードによる期待値
| アップカード | 期待される 価値 |
| 2 | 9.10% |
| 3 | 12.38% |
| 4 | 15.85% |
| 5 | 19.65% |
| 6 | 23.40% |
| 7 | 14.40% |
| 8 | 5.82% |
| 9 | -4.06% |
| 10 | -17.36% |
| あ | -33.78% |
したがって、ディーラーにアップカードとして6を選ぶことができるなら、それは6を選ぶべきであるというのは確かに真実です。6はディーラーにとって不利であるだけでなく、プレイヤーにとっても不利です。総合的に考えると、シューから1枚カードを取り除けるなら、5を選ぶべきです。
友人がカジノのウェブサイトに100ドルを入金しました。すると300ドルのボーナスが付いて、合計400ドルになりました。ボーナスを使い切るには8,000ドルを賭けなければなりませんでした。計算してみたところ、カジノ側のアドバンテージはボーナス額を超えず、プレイヤーはボーナスを使い切るまで有利な立場にあることが分かりました。彼は1週間プレイを続け、最終的に5,500ドル以上を獲得しました。こんな話は初めて聞きました。どれくらいの確率なのでしょうか？理解できません。宝くじに当たるのと同じくらい、ほとんど不可能に思えます。どう思いますか？
負けを恐れないなら、賭け条件を回避する良い方法は、早い段階で積極的に賭け、大勝ちを狙うか、失敗しても構わないと考えることです。もし大勝ちしたら、より慎重に賭け条件をクリアしましょう。しかし、それはあなたの質問ではありません。ハウスエッジがないと仮定した場合、400ドルを5,900ドル（賞金5,500ドル）にする確率は、400/5,900 = 6.78%です。もちろん通常はハウスエッジはありますが、賢くプレイすればそれを非常に低く抑えることができます。つまり、6.78%は確率の上限と言えるでしょう。
クラップスプレイヤーとして、チュニカにある、よりプレイヤーフレンドリーなクラップレスバージョンを楽しんでいます。彼らのバイベットでは、勝ったベットにのみヴィグが支払われます。そこで、10ドルの3または11でヴィグ控除後29ドル、あるいは10ドルの2または12でヴィグ控除後59ドルになる可能性について知りたいです。
3または11に10ドル賭けた場合、配当は29.50ドル、2または12に賭けた場合59.50ドルとなります。ハウスエッジは3または11の場合1.25%、2または12の場合0.71%です。
同じペイテーブルと額面金額を想定して、10 プレイ ポーカーを 1,000 ハンド、またはシングル プレイ ポーカーを 10,000 ハンドプレイするとしたら、戦略と期待値は同じだとわかっていますが、変動性に違いはあるでしょうか?
はい。9/6ジャックス・オア・ベターをプレイしていると仮定しましょう。最終ハンドあたりの分散はn*1.966391 + 17.548285です（nはプレイ回数）。つまり、10プレイの場合のハンドあたりの分散は10*1.966391 + 17.548285 = 37.2122、1プレイの場合は1*1.966391 + 17.548285 = 19.51468です。10プレイの場合、最初の1,000ハンド、つまり合計10,000ハンドの分散は10,000*37.2122 = 372,122です。1プレイの場合、10,000ハンドの分散は10,000*19.51468 = 195,149です。しかし、ここで議論すべきは標準偏差、つまり分散の平方根だと思います。10人プレイの10,000ハンドの標準偏差は372,122 × 0.5 = 610.02です。1人プレイの10,000ハンドの標準偏差は195.149 × 0.5 = 441.75です。最終的なハンドの合計が同じであれば、9/6ジャックス・オア・ベターでは、10人プレイは常に38.1%変動が大きくなります。詳しくは、 n人プレイビデオポーカーの標準偏差に関するセクションをご覧ください。
自分に正直になれば間違いはない
浮気をしている彼氏についての質問に対して、いつも同じアドバイスを何度も繰り返していることに気づきました。同じことを繰り返さないように、以下に一般的なアドバイスをいくつか示します。これ以降、以下のアドバイスが当てはまると思われる質問にはお答えしません。
このサイトのすべてのギャンブルに関するアドバイスの根底にあるのは、決断を迫られた際には、最も高い期待値をもたらす選択肢を選ぶということです。これは、恋人、夫、妻を探す際にも当てはまります。あなたが合理的に期待できる、最も高い期待値を持つ人を探しましょう。人間の期待値はどのように測るべきでしょうか？マーティン・ルーサー・キング・ジュニアの言葉を借りれば、まずその人の人格の中身を見るべきだと思います。
浮気が発覚した人を許すべきかどうか、よく聞かれます。一般的には、許さないことをお勧めします。これは、相手が道徳心の低い人であるという明らかな兆候です。もしかしたら、これまで何年も幸せに暮らしていて、それが一度きりの出来事に思えるなら、許す必要もないかもしれません。しかし、二度と許してはいけません。
不正行為に疑いがある場合は、証拠なしに非難してはいけません。あらゆる可能性について質問しても、自白につながる可能性は低く、間違っていた場合、ただ信用できないうるさい人だと思われてしまうだけです。ですから、疑わしい時は口を閉ざし、目と耳を大きく開いてください。
「残るべきか、それとも辞めるべきか」「どちらを選ぶべきか」といった疑問に対する私の一般的なアドバイスは、自分の脳があなたに指示することに従うことです。短期的には難しい決断になることが多いかもしれませんが、長期的には悪い人間関係に時間を浪費することが少なくなり、より質の高い候補者と出会える可能性が高まります。
よくある質問の一つは、別れ方についてです。私のアドバイスは、別れは冷たく、清廉潔白であるべきだということです。友情などというナンセンスなことはやめましょう。まだ友達でいられるなら、なぜ別れるのでしょうか？もし既に別れていて、あなたがそれで満足しているのに、相手が諦めてくれないなら、彼を誘惑したり、甘えさせたりしないでください。電話もメールも、どんな形であれ連絡を取らないように伝え、もし彼が連絡してきたとしても返信しないでください。
「自分に正直になれば、間違いはない」 - ユーリズミックサー