テレビゲームショー - よくある質問
正確にはギャンブルではありませんが、『ザ・プライス・イズ・ライト』のゲームショーで、ビッグホイールを回す際に最後のスピナーでない場合の最適な戦略についていつも考えていました。スピンを完全にコントロールできない(結果は完全にランダム)、$0.05から$1.00までの5セント刻み、1回または2回のスピンを合計、$1.00を超えることはできないという条件下で、次のスピナーに勝つ確率を最大化するために、どの金額で2回目のスピンをやめるべきでしょうか?
最初のプレイヤーは、最初のスピンが65セント以下の場合、再度スピンする必要があります。
以下のいずれかの条件が真の場合、2番目のプレイヤーは再度スピンする必要があります。
- 彼のスコアは最初のプレイヤーのスコアより少ない。
- 彼のスコアは50セント以下である。
- 彼のスコアは65セント以下で、最初のプレイヤーと同点である。
「ザ・プライス・イズ・ライト」のPlinkoゲームに最適な戦略は何ですか?
左から右の順に、賞金は 100 ドル、500 ドル、1000 ドル、0 ドル、10000 ドル、0 ドル、1000 ドル、500 ドル、100 ドルです。完璧な分析を行うには、ボード上のペグの正確な配置を知る必要がありますが、ボードを目視しただけ (上記リンクを参照) では、プレーヤーは 10,000 ドルの賞金の真上にパックを落とすべきであると強く感じます。2 つのゼロで縁取られているとはいえ、他のすべての賞は最高賞金に比べると見劣りします。したがって、プレーヤーの戦略は、真上にパックを落とすことで最高賞金の確率を最大化することです。自分の仮説を確認するか否定するかを調べるために検索したところ、このゲームの研究に関するリンクが多数見つかりました。これ ( www.amstat.org/publications/jse/v9n3/biesterfeld.html ) は優れたリンクの 1 つで、私の結論と一致しています。パックを真ん中に落とした場合の期待値は 2,557.91 ドル、真ん中のどちらかの側に落とした場合の期待値は 2,265.92 ドルで、中心から離れるにつれて徐々に減少していくと述べられています。
ゲーム番組Let’s Make a Deal には、3つのドアがあります。例として、2つのドアが山羊を表しており、1つのドアが新しい車を表しているとします。ホストのモンティ・ホールはドアを選ぶために2人の出場者を選びます。モンティが最初にドアを開けるたびにヤギが現れます。今回は最初の出場者のものだったとしましょう。モンティが実際にこれを行ったことはありませんが、モンティが他の競技者にこの時点でドアを他の未開封のドアに切り替える機会を提供した場合はどうなりますか。彼は切り替える必要があるのでしょうか?
はい! この問題の鍵は、ホストがヤギでドアを開ける運命にあるということです。 彼はどのドアに車があるかを知っているので、プレイヤーがどのドアを選んでも、最初にヤギを明らかにすることができます。 この問題は「モンティ・ホールのパラドックス」として知られています。 それについての混乱の多くは、質問が組み立てられたときに、ホストが車がどこにあるかを知っていて、常に最初にヤギを明らかにすることが誤って明確にされていないことが多いためです. 私は責任のいくつかを置くと思います マリリン ヴォス サバント, 彼女のコラムで質問をひどく組み立てた. 賞品がドア 1 の後ろにあると仮定しましょう。プレーヤー (2 番目の競技者) が切り替えない戦略を持っていた場合、次のようになります。
- プレーヤーがドア 1 を選択 --> プレーヤーの勝ち
- プレーヤーがドア 2 を選ぶ --> プレーヤーが負ける
- プレーヤーがドア 3 を選ぶ --> プレーヤーが負ける
以下は、プレーヤーが切り替えの戦略を持っていた場合に何が起こるかです。
- プレーヤーがドア 1 を選択 --> ホストがドア 2 または 3 の後ろにヤギを表示 --> プレーヤーが別のドアに切り替える --> プレーヤーが負ける
- プレイヤーがドア 2 を選ぶ --> ホストがドア 3 の後ろにいるヤギを明らかにする --> プレイヤーがドア 1 に切り替える --> プレイヤーが勝つ
- プレイヤーがドア 3 を選択 --> ホストがドア 2 の後ろにヤギを出現させる --> プレイヤーがドア 1 に切り替える --> プレイヤーの勝利
したがって、プレーヤーを切り替えないことで、勝つチャンスは 1/3 になります。 プレーヤーを切り替えることで、2/3 の確率で勝つことができます。 したがって、プレイヤーは間違いなく切り替える必要があります。
モンティ ホールのパラドックスの詳細については、ウィキペディア の記事をお勧めします。
私の質問は、「2つの封筒のパラドックス」として知られる問題についてです。あなたはゲーム番組に出演しています。目の前に2つの封筒があり、それぞれに金額は不明です。片方の封筒にはもう片方の2倍の金額が入っていると告げられます。あなたはどちらかの封筒を選ぶように言われます。あなたは片方を選びます。そこには5万ドルが入っていました。そして、選んだ封筒をそのままにするか、もう片方の封筒と交換するかを尋ねられます。交換すべきでしょうか?交換できることが事前に分かっていれば、最終的に欲しい封筒を選ぶだけなので、交換するかどうかは問題ではありません。しかし、封筒を選んだ後に交換について知ることになるので、最初の選択と交換の選択肢は2つの独立した事象ですよね?つまり、交換するかどうかを決める際に、もう片方の封筒には現在持っている金額の2倍か半分の金額が入っていることになります。つまり、10万ドルか2万5千ドルのどちらかです。どちらかが起こる確率が50%なので、もう片方の封筒の期待値は6万2500ドルです。一般的に言えば、xを最初に選択した金額とすると、もう一方の封筒のEVは1.25倍になります。したがって、スワップすることは常に正しいと言えます。これで合っていますか?ありがとうございます。
この問題にはよく精通しています。私のウェブサイト「数学の問題」の6番でこの問題を取り上げています。そこでは、最初の封筒を全く見ないことも含め、一般的なケースを取り上げています。しかし、あなたの質問に答えるには、ゲームが行われている場所を無視することはできません。あなたは「ゲームショー」だとおっしゃいました。ほとんどのゲームショーでは、5万ドルの賞金は立派なものです。「ザ・プライス・イズ・ライト」の出場者で、その金額を獲得する人はほとんどいません。「フー・ウォンツ・トゥ・ビー・ア・ミリオネア」の参加者で、その金額を獲得する人は50%にも満たないのではないでしょうか。一方、ゲームショーでは2万5000ドルの賞金獲得は珍しくありません。「ザ・プライス・イズ・ライト」では、約2万5000ドル相当の車が日常的に当たります。「フー・ウォンツ・トゥ・ビー・ア・ミリオネア」では、3万2000ドルの賞金獲得は珍しくありません。「ジェパディ」の1番組あたりの平均賞金は約2万5000ドルです。あのケン・ジェニングスでさえ、74回の優勝で平均3万4091ドルしか獲得していません。つまり、私が言いたいのは、ゲームショーにとって5万ドルは立派な勝利であり、10万ドルの勝利は2万5000ドルの勝利よりもはるかに少ないということです。ゲームショーの専門家として、もう一方の封筒には10万ドルよりも2万5000ドルが入っている可能性が高いと私は考えています。ですから、あなたの例では5万ドルを保管しておく方が良いと思います。また、もう一方の封筒に半分または2倍の金額が入っている確率が50/50であるとは決して想定できないことも示しています。金額を確認し、それがプレイされる会場の状況と照らし合わせれば、切り替えについて賢明な判断を下すことができます。1.25倍という議論はもはや無意味です。
オーストラリアで大人気で、間もなくイギリスでも放送されるゲーム番組「Deal or No Deal」について質問です。出場者は26個の番号付きブリーフケースを見せられます。それぞれのブリーフケースには、50セントから20万ドルまでの金額が隠されています。
- 0.50ドル
- 1ドル
- 2ドル
- 5ドル
- 10ドル
- 25ドル
- 50ドル
- 75ドル
- 100ドル
- 150ドル
- 250ドル
- 500ドル
- 750ドル
- 1,000ドル
- 1,500ドル
- 2,000ドル
- 3,000ドル
- 5,000ドル
- 7,500ドル
- 1万ドル
- 1万5000ドル
- 3万ドル
- 5万ドル
- 7万5000ドル
- 10万ドル
- 20万ドル
出場者はブリーフケースの中から1つを選び、それを自分のスーツケースとします。残りのスーツケースを開けることで、消去法を用いて、自分のスーツケースにいくら入っているか、あるいは「銀行オファー」を受ける方が賢明かどうかを判断します。銀行オファーは、残りのブリーフケースの算術平均に基づいていますが、必ずしも等価ではありません。つまり、残っているブリーフケースのほとんどが高額の場合、出場者のブリーフケースは高額である可能性が高いため、銀行オファーは高額になります。逆に、運が悪く、より高額なブリーフケースを開けてしまった場合、銀行オファーは低額になります。もしあなたがこのゲームの出場者だったら、どのような戦略を取るべきでしょうか?数学に頼らない直感的な戦略としては、銀行オファーを無視し、20万ドルが開けられて消えるまで、あるいは10万ドルと7万5千ドルの両方が開けられて消えるまで、ケースを開け続けるという戦略があります。このゲームの数学は何ですか、ウィザード?
「ディール・オア・ノー・ディール」がアメリカでスタートしました。ルールはアメリカと同じですが、賞金は以下のように100万ドルまで上がります。
- 0.01
- 1
- 5
- 10
- 25
- 50
- 75
- 100
- 200
- 300
- 400
- 500
- 750
- 1000
- 5000
- 10000
- 25000
- 50000
- 75000
- 100000
- 200000
- 300000
- 400000
- 500000
- 750000
- 100万
ゲームの流れは次のとおりです。
- プレイヤーは自分でケースを1つ選びます
- プレイヤーは残りの 25 個のケースのうち 6 個を開けます。
- 銀行家がオファーを出します。
- プレイヤーが拒否した場合、残りの 19 個のケースのうちさらに 5 個を開きます。
- 銀行家がオファーを出します。
- プレイヤーが拒否した場合、残りの 14 個のケースのうちさらに 4 個を開きます。
- 銀行家がオファーを出します。
- プレイヤーが拒否した場合、残りの 10 個のケースのうちさらに 3 個を開きます。
- 銀行家がオファーを出します。
- プレイヤーが拒否した場合、残りの 7 つのケースのうちさらに 2 つを開きます。
- 銀行家がオファーを出します。
- プレイヤーが拒否した場合、残りのケースをさらに 1 つ開きます。
- プレイヤーがオファーを受け入れるか、最後の未開封のケースを手に入れるまで、手順 11 と 12 を繰り返します。
次のグラフは、プレイヤーの期待値とバンカーのオファーを示しています。
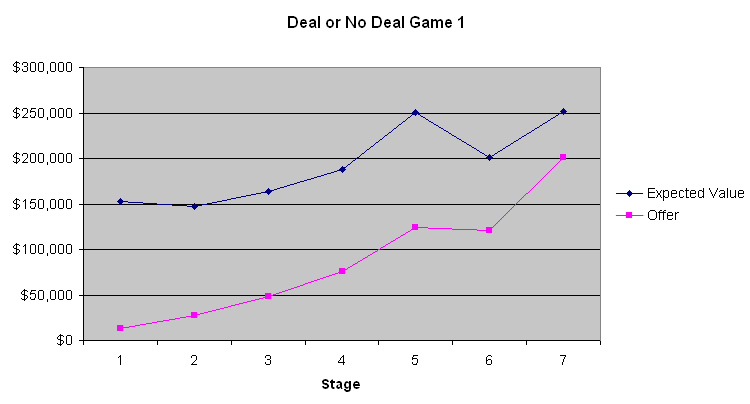
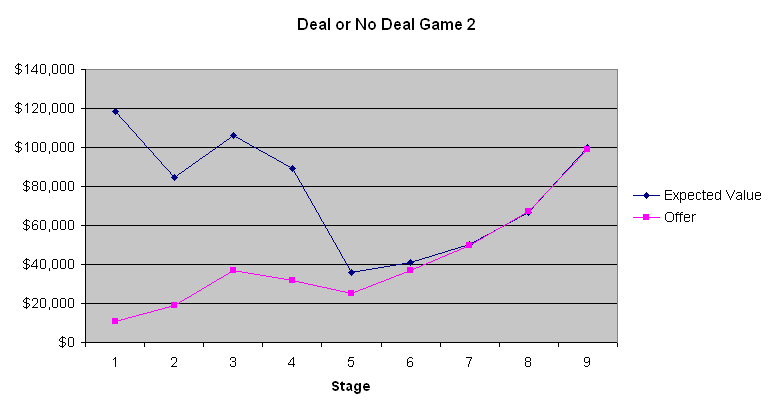
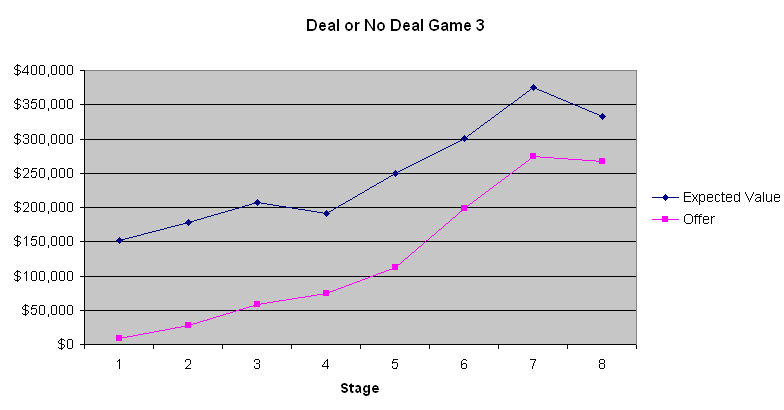
これら3つのチャートから最も明白なことは、最初の4~6回の銀行のオファーがひどい取引だということです。平均的なスーツケースには、開けられる前に131,477.54ドル入っています。最初の段階で9,000ドルから13,000ドルしか提示しないのは、愚か者だけが行う取引です。しかし、徐々にオファーは良くなっていきます。ゲーム2では、プレイヤーの期待値がかなり低かったゲーム終盤では、期待値が銀行のオファーとほぼ同じだったことがわかります。しかし、期待値が高かったゲーム1と3では、銀行は明らかに、高額が絡むとほとんどの人がリスクを嫌う性質を利用しようとしていました。それが重要かどうかはわかりませんが、ゲーム2の出場者は大金を獲得したいギャンブラーのように見えました。電話で銀行員と連絡を取っている司会者のコメントに基づくと、銀行員は出場者の言動を慎重に見ているように見えます。私が銀行員の立場だったら、同じように行動するでしょう。
プレイヤーがリスク回避型でもリスクを好む型でもなく、税金の影響も考慮に入れないのであれば、残りのスーツケースの平均を超えるまで銀行側の申し出を拒否し続けるべきです。ほとんどの人にとって、所得税法の累進課税は取引を受け入れることを有利にしています。以前にも述べたように、お金の価値は金額の対数に比例すると大まかに言っておきます。つまり、ゲーム開始時に持っている資産が多ければ多いほど、銀行側の申し出を拒否する賭けに出る傾向が強くなるはずです。これほど巨額の資金が絡むゲームでは、誰にでも当てはまる戦略は存在しません。しかし、最初の4~6件の申し出を拒否し、その後は状況に応じて(意図的に)申し出を受け入れるべきだと、私はかなり自信を持って言えます。
リンク:
「Deal or No Deal」はNBC.comで視聴できます。
過去の番組のアーカイブ。
「ディール・オア・ノー・ディール」を観ています。バンカーの「オファー」は、ケースの残り金額をケースの数で割ったもの(四捨五入の多少の誤差あり)だと気づきました。このゲームに何か戦略はあるのでしょうか?それとも「ディール」はいつでもOKなのでしょうか?ケースをいくつ開けるかなどによっても変わるのでしょうか?
「ディール・オア・ノー・ディール」の開始時に、100万ドルのケースを選ぶ確率は26分の1です。1つを除くすべてのケースを除外した後、私のケースに100万ドルが含まれている確率はどれくらいでしょうか。50-50ですか、それともまだ26分の1ですか?
50-50
いいえ。この件については多くの人が反論しています。多くの著者は、追加情報が入っても確率は変わらないと主張しています。つまり、確率が26分の1から始まったなら、その確率は変わらないということです。ベッティングシステムのセールスマンの言うこととは反対に、追加情報が入ってくると確率は確かに変わる可能性があります。ここで基本的な確率を教えたいわけではありませんが、条件付き確率やベイズの定理を扱った大学レベルの数学の教科書なら、この話題はきちんと説明されているはずです。
Let's Make a Deal で何が起こったか説明しましょう。参加者は 3 枚のカーテンのうち 1 枚を選びます。1 枚には非常に価値のある賞品が入っており、他の 2 枚には小さな賞品が入っています。議論のために、1 枚のカーテンの後ろには車があり、他の 2 枚のカーテンの後ろにはヤギがいるとします。するとモンティは常に、繰り返しますが常に、選ばれなかった 2 枚のカーテンのうち 1 枚を開けてヤギを出します。何百もの番組を経て、これはモンティ ホール (司会者) が車がどこにあるかを知っていて、わざとヤギの入ったカーテンを開けたということを意味します。明らかに、参加者がカーテンを選んだときに車が入っている確率は 1/3 で、選ばれなかった 2 枚のカーテンのうち 1 枚に車が入っている確率は 2/3 です。するとモンティは、ゴールが入っている選ばれなかったカーテンを開けるように運命づけられているのです。運命づけられているというのがここでは重要なキーワードです。モンティはこの段階で参加者のカーテンを開けることができないため、参加者のカーテンから車が出てくる確率は 1/3 のままです。選ばれなかったカーテンが車を出す確率は2/3のままですが、今は片方のカーテンに車が描かれています。つまり、ヤギが出てきた後、プレイヤーのカーテンに車が出る確率は1/3、もう片方の開いていないカーテンに車が出る確率は2/3となり、カーテンを切り替えるのは賢明な選択となります。
以下の表は、すべての可能な結果を示しています。プレイヤーが車のカーテンを選んだ場合、モンティはカーテンを勝手に開けました。カーテンを切り替えない場合は勝率が1/3、切り替えた場合は勝率が2/3であることがわかります。
取引をしましょう
| プレーヤー 選択する | 車 | カーテン オープン | 確率 | 勝利 切り替え |
| 1 | 1 | 1 | 0% | 該当なし |
| 1 | 1 | 2 | 5.56% | 北 |
| 1 | 1 | 3 | 5.56% | 北 |
| 1 | 2 | 1 | 0% | 該当なし |
| 1 | 2 | 2 | 0% | 該当なし |
| 1 | 2 | 3 | 11.11% | はい |
| 1 | 3 | 1 | 0% | 該当なし |
| 1 | 3 | 2 | 11.11% | はい |
| 1 | 3 | 3 | 0% | 該当なし |
| 2 | 1 | 1 | 0% | 該当なし |
| 2 | 1 | 2 | 0% | 該当なし |
| 2 | 1 | 3 | 11.11% | はい |
| 2 | 2 | 1 | 5.56% | 北 |
| 2 | 2 | 2 | 0% | 該当なし |
| 2 | 2 | 3 | 5.56% | 北 |
| 2 | 3 | 1 | 11.11% | はい |
| 2 | 3 | 2 | 0% | 該当なし |
| 2 | 3 | 3 | 0% | 該当なし |
| 3 | 1 | 1 | 0% | 該当なし |
| 3 | 1 | 2 | 11.11% | はい |
| 3 | 1 | 3 | 0% | 該当なし |
| 3 | 2 | 1 | 11.11% | はい |
| 3 | 2 | 2 | 0% | 該当なし |
| 3 | 2 | 3 | 0% | 該当なし |
| 3 | 3 | 1 | 5.56% | 北 |
| 3 | 3 | 2 | 5.56% | 北 |
| 3 | 3 | 3 | 0% | 該当なし |
一方、「ディール・オア・ノー・ディール」では何も決まっていません。「ディール・オア・ノー・ディール」で残額がそれぞれ0.01ドル、1ドル、100万ドルだったと仮定してみましょう。残り3つのケースで、開封したケースに100万ドルが入っている可能性はあります。以下の表は、残り3つのケースで起こり得る結果を示しています。プレイヤーは自分でケースを開けることはできないことに注意してください。
取引か取引なしか
| プレーヤー 選択する | 百万ドル | 場合 オープン | 確率 | 勝利 切り替え |
| 1 | 1 | 1 | 0% | 該当なし |
| 1 | 1 | 2 | 5.56% | 北 |
| 1 | 1 | 3 | 5.56% | 北 |
| 1 | 2 | 1 | 0% | 該当なし |
| 1 | 2 | 2 | 5.56% | 絶望的 |
| 1 | 2 | 3 | 5.56% | はい |
| 1 | 3 | 1 | 0% | 該当なし |
| 1 | 3 | 2 | 5.56% | はい |
| 1 | 3 | 3 | 5.56% | 絶望的 |
| 2 | 1 | 1 | 5.56% | 絶望的 |
| 2 | 1 | 2 | 0% | 該当なし |
| 2 | 1 | 3 | 5.56% | はい |
| 2 | 2 | 1 | 5.56% | 北 |
| 2 | 2 | 2 | 0% | 該当なし |
| 2 | 2 | 3 | 5.56% | 北 |
| 2 | 3 | 1 | 5.56% | はい |
| 2 | 3 | 2 | 0% | 該当なし |
| 2 | 3 | 3 | 5.56% | 絶望的 |
| 3 | 1 | 1 | 5.56% | 絶望的 |
| 3 | 1 | 2 | 5.56% | はい |
| 3 | 1 | 3 | 0% | 該当なし |
| 3 | 2 | 1 | 5.56% | はい |
| 3 | 2 | 2 | 5.56% | 絶望的 |
| 3 | 2 | 3 | 0% | 該当なし |
| 3 | 3 | 1 | 5.56% | 北 |
| 3 | 3 | 2 | 5.56% | 北 |
| 3 | 3 | 3 | 0% | 該当なし |
「ディール・オア・ノー・ディール」表が示すのは、残り3つのケースでプレイヤーが100万ドルのケースを開ける確率は1/3(勝つ見込みなし)、切り替えたプレイヤーが勝つ確率は1/3、切り替えたプレイヤーが負ける確率は1/3であるということです。つまり、ケースを切り替える確率は同じです。残り2つのケースになると、それぞれのケースに高額賞金が入っている確率は50/50になります。
さあ、また「ディール・オア・ノー・ディール」の質問の時間です。銀行員による全ての取引とセリーヌ・ディオンのゲスト出演の後、50万ドルと100万ドルのスーツケースが2つ残ったとしましょう。銀行員の提示額はおそらく75万ドルより少し少ないでしょう。どちらを選びますか?もし残った2つのブリーフケースが0.01ドルと100万ドルだったらどうしますか?これはギャンブラーかどうかの問題で、オッズとは関係ないと思います。なぜ質問するかというと、100万ドルを当てられる人がいるのか(たとえ魔法のブリーフケースを選んだとしても)疑問に思うからです。
賞金が人生を変えるほどの額になった場合、賢明なプレイヤーは期待値の最大化を犠牲にして保守的にプレイするべきです。良い戦略とは、期待される幸福度を最大化することです。幸福度を測る良い関数は、総資産の対数だと私は考えています。例えば、10万ドルの資産を持つ人が、0.01ドルと100万ドルの2つのケースを提示されたとします。「ノーディール」を選択した場合の期待幸福度は、0.5*log(100,000.01ドル) + 0.5*log(1,100,000ドル) = 5.520696です。bを、プレイヤーが受け取ることに無関心な銀行のオファーとします。
log(b) = 5.520696
b = 10 5.520696
b = 331,662.50ドル。
したがって、この仮想プレイヤーは銀行が提示する331,662.50ドルには無関心であるはずです。ゲーム開始時の資産が少ないほど、より保守的にプレイするべきです。通常、ゲーム終盤では銀行の提示額は期待値に近くなりますが、場合によっては少し多くなることもあります。プレイヤーが100万ドルを獲得できる合理的なケースは、ゲーム開始時に多額の資産を保有していた場合、または銀行の提示額が異常にケチだった場合のみです。プロデューサーは勤勉な中流階級の人々を好むようなので、多額の金額が絡むゲームで軽率な行動をとるような人物はまず見当たりません。また、ゲーム終盤で銀行が期待値の90%を下回る提示額を提示するのを見たことはありません。100万ドルを獲得する人物が見られるのは、止まらないギャンブラーが番組に出演したときでしょう。そうなったら、私は銀行側を応援するでしょう。
これは最近初めて見た「ディール・オア・ノー・ディール」の続編です。あなたの分析では、銀行側はスーツケースの中のお金の価値を知らないと仮定しています。しかし、私が見た番組では、終盤で両方の出場者が価値の高いケースを選択し、期待値(EV)を上回る取引が提示されました(または、片方は既に棄権していたため、提示されたはずでした)。最も極端なケースでは、残された金額が50万ドルと75万ドルだったにもかかわらず、あるプレイヤーは68万7千ドルを提示されたはずでした。この状況に対する唯一の合理的な説明は、銀行側がプレイヤーのスーツケースの価値を知っており、提示された取引はそれに基づいているということです。
あくまでも私の意見ですので、返信は必要ありません。
返事を期待していないことに感謝します。でも、私は通常、ゲーム番組の質問には返事をします。番組では毎回、ケースの中の金額はランダムに配置され、ハウイーもバンカーも結果を知ることはないと主張しています。これは「Let's Make a Deal」では決して主張されていませんでした。モンティ・ホールが明らかに知っていたからです。私も、特に大きな金額が絡んでいる場合、バンカーが最後のオファーとして予想以上の金額を提示するのを見たことがあります。私の強い意見では、これはバンカーがプレイヤーのケースの中身を知っているからではありません。1950年代には、 「21」などの番組で八百長が行われたことが発覚し、大スキャンダルとなりました。銀行のオファーで賞金を着服するために、成功している番組、そしてすべてのゲーム番組の誠実さを台無しにする説得力のある理由はありません。
銀行家が残りのケースの平均よりも高い金額を提示することがある理由について、3 つの理論を挙げることができます。
- この番組では、銀行員がオフィスで金銭に汗水垂らして働いている様子を描いています。ハウィー・マンデルは、銀行員の気分や口調について頻繁にコメントしています。銀行員をリスク回避型の会計士、つまり大きな利益を得るリスクを冒すよりも損失を抑えることを好む人物として描くことで、この番組はよりドラマチックになっているのかもしれません。
- 真のバンカーはまさにリスク回避型です。これは私の専門分野から外れますが、私の理解では、ゲーム番組やリアリティ番組は通常、テレビ局とは独立した会社によって制作されています。これらの小規模な制作会社は、出場者が高額賞金を獲得するリスクを軽減するために保険会社を探します。そのような場合、保険会社こそが真のバンカーとなり、番組におけるバンカーの行動に影響を与えている可能性があります。このような奇妙な番組に保険をかける保険会社は巨大企業ではなく、多額の賞金が絡む場合は安全策を講じる傾向があるのかもしれません。
あなたの例では、バンカーのオファーは期待値を9.92%上回っていました。もしバンカーがケリー基準に従っていたなら、このようなオファーは総額わずか782,008ドルで行われていたはずです。これは最高賞金を下回っています。自尊心のある保険会社なら、そこまで保守的になるはずがありません。明らかに、この理由だけでは、あなたの例のオファーを正当化することはできません。
- この番組は、出場者を愚かで強欲に見せようとしている。「5年生より賢い?!」やトゥナイトショーの「Jaywalking」のような番組は、雑学クイズに苦手意識を持つ人たちを笑わせることに満足感を得られなければ成功しなかっただろう。 「Friend or Foe」や「The Weakest Link」は、人間の本性にある強欲さを露呈させる点で傑出していた。出場者が予想以上の金額のオファーを断り、彼の場合は低い金額で帰るのを見ると、正直言って、他人の不幸を喜ぶような気持ちになった。
理由はこれら 3 つの理由の組み合わせであると考えがちですが、主に 3 番目の理由です。
ここで答えを終わらせたら、きっとコメントが寄せられ、架空の銀行員のオファーが本当に行われたのか疑問視されるでしょう。つまり、ドラマチックな効果を狙って誇張されているのではないかという疑念です。私は13のゲームの詳細を記録しました。そのうちの1つでは、残り3つのケース(1,000ドル、5,000ドル、50,000ドル)で、平均は18,667ドル、オファーは21,000ドルでした。これは予想値を12.5%上回っています。別の番組では、残り2つのケース(400ドルと750,000ドル)で、平均は375,200ドル、オファーは400,000ドルでした。これは予想値を6.6%上回っています。ですから、架空のオファーの信憑性に疑問を抱く理由はないと思います。
リンク:
ディール・オア・ノー・ディールの計算式: このページでは、ディール・オア・ノー・ディール Web サイトの無料ゲームに基づいて、バンカーのオファーを計算するための古い計算式と新しい計算式を示します。
それぞれの人の立場で、ファイナル ジェパディで次のスコアにいくら賭けますか。
プレイヤーA: 10,000ドル
プレイヤーB: 8,000ドル
プレイヤーC: 3,500ドル
まず、いくつか仮定を立ててみましょう。まず、3人の参加者は、提示された表の正解確率以外、ファイナル・ジェパディにおける賭け行動について事前の知識を持っていないと仮定します。次に、カテゴリーを知っていても何の役にも立たないと仮定します。さらに、3人の参加者全員が勝利を目指しており、同点に陥った場合、他の参加者を引きずりたくないと考えていると仮定します。
まずプレイヤーCから始めましょう。彼は、AがBの予想が当たればBを上回るために$6001を賭けるかもしれないと予想するはずです。しかし、Aが間違っていたら、Cの賭け金は$3999に下がります。このような状況でAに勝つには、Cが少なくとも$500を賭け、かつ正しく予想する必要があります。しかし、私の意見では、勝つために正しく予想しなければならないのであれば、大金を賭けた方が良いでしょう。ですから、もし私がCだったら、Cはすべてを賭けるでしょう。
Bは大きく賭けるか小さく賭けるかで迷っています。Cが当たってもCを上回るためには、小さく賭ける場合は999ドル以下に抑えるべきです。小さく賭ける利点は、どんな状況でもCを上回ること、つまりAが大きく賭けて外れることを期待できることです。大きく賭ける利点は、Aが小さく賭けるか、大きく賭けて外れるかのどちらかを期待できることですが、どちらの場合もBが当たっていることが条件となります。
Aは基本的にBと同じ展開を期待しています。Aのスモールベットは$0から$1000までの範囲で設定でき、Bが$999を賭けた場合、Aの賭け金はBの賭け金より高くなります。ビッグベットは$6001に設定すべきです。Aが当たれば確実に勝ちますが、Bがビッグベットし、3人全員が外れた場合でも、Aの賭け金がBの賭け金を上回るようにするためです。
正解と不正解の8通りの結果の確率を推測するために、j-archive.com(現在は利用できません)にあるシーズン20から24までの「ファイナル・ジェパディ」の結果を見ました。結果は以下の通りです。プレイヤーAがトップ、プレイヤーBが続き、プレイヤーCが最下位です。
最終的な危機における可能性のある結果
| プレイヤーA | プレイヤーB | プレイヤーC | 確率 |
| 右 | 右 | 右 | 21.09% |
| 右 | 右 | 間違っている | 9.73% |
| 右 | 間違っている | 右 | 10.27% |
| 間違っている | 右 | 右 | 8.74% |
| 右 | 間違っている | 間違っている | 13.33% |
| 間違っている | 右 | 間違っている | 10.27% |
| 間違っている | 間違っている | 右 | 8.63% |
| 間違っている | 間違っている | 間違っている | 17.92% |
私のサイトmathproblems.infoの問題 192 で説明しているようなゲーム理論の論理を使用すると、A と B は次のように戦略をランダム化する必要があることがわかります。
プレイヤーAは、73.6%の確率で大金を賭け、26.4%の確率で小金を賭けるべきです。
プレイヤー B は、67.3% の確率で大金を賭け、32.7% の確率で小金を賭けるべきです。
プレイヤーCは100.0%の確率で大金を賭けるべきです。
この戦略に従えば、各プレイヤーの勝利の確率は次のようになります。
プレイヤーA: 66.48%
プレイヤーB: 27.27%
プレイヤーC: 6.25%
ちなみに、上記の表によると、トップのプレイヤーが最終問題に正解する確率は54.4%、2位のプレイヤーが49.8%、3位のプレイヤーが48.7%です。全体の確率は51.0%です。
実務上の注意点として、プレイヤーは賭けの行動についてある程度の知識を持っています。私の判断では、プレイヤーは数学的に正当化されるよりも頻繁に、高額ベットをする傾向があります。興味深いことに、デイリーダブルでの賭けは、数学的に正当化されるよりも保守的すぎると感じています。ケン・ジェニングスが好成績を収めた理由の一つは、ダブルダブルでの積極的な賭けでした。いずれにせよ、もし私が実際に番組に出演していたら、他の二人のプレイヤーは積極的に賭けるだろうと予想します。つまり、私の実際の賭け金は、Aが6000ドル(Bに配慮)、Bが0ドル、Cが3495ドル(Aが愚かにも1ドル以外を賭けて間違った場合に備えて、少し賭けない金額を残す)になります。
実際の会場でどうやってランダムな数字を抜き出すのかと誰かが私に異議を唱える前に、時計の秒針を使って 1 から 60 までのランダムな数字を抜き出すというスタンフォード ウォンの戦略を提案したいと思います。
英国で「カラー・オブ・マネー」という新しいゲーム番組が初放送されました。参加者は1人だけ。目標金額がランダムに与えられ、その範囲は5万5000ポンドから7万9000ポンドとされています。参加者は20台のATMから10台を選び、1台につき1000ポンドから2万ポンドまで、1000ポンドずつ均等に金額を加算していきます。参加者がATMを選ぶと、1000ポンドから1000ポンドずつ、金額が加算されていきます。
プレイヤーはいつでも「ストップ!」と叫ぶことができ、画面に表示されている金額を賭けることができます。プレイヤーが時間内に止めず、マシンのお金がなくなった場合は、賭け金はゼロになります。ホステスが、残りのマシン数、獲得できる金額、マシン1台あたりの勝利に必要な平均金額、マシンに残っている金額などの統計情報を提供します。
プレイヤーは「ギャップを活かす」ことができます。例えば、4,000ポンド、5,000ポンド、6,000ポンドといった順番にマシンが選ばれると、3,000ポンドの水準を超えた時点で7,000ポンドに達することが保証されます。そこで質問なのですが、プレイヤーはどのような戦略を取るべきでしょうか?
これは何週間もかけて分析できそうな類のものです。残念ながら、「魔法使いに質問」の質問が大量に滞っていたため、あなたのメッセージを読んだのは投稿から3ヶ月近く経ってからでした。Wikipediaのページによると、あの番組は失敗に終わり、打ち切られたようですね。それでも、興味深い問題ですね。
ホステスが、残り1台あたりの平均ゲーム数を教えてくれるんです。何時間も考えてみましたが、必要な平均数より25%ほど高い停止目標を設定する以外に良い案は思いつきません。これはあくまで推測なので、最適解の証明は求めないでください。ご指摘の通り、ギャップも踏まえ、既に選ばれた数に達する直前で停止しないようにしてください。
残り2台になった場合、必要な金額の合計が13,000ポンド以下の場合は、最後から2番目のマシンで全額購入するようにします。14,000ポンド以上の場合は、次のマシンで半額購入するようにします。
もしこの番組が復活したら、イギリスの読者の皆さんに教えていただけると嬉しいです。これは、偶然にも(あるいはそうでなかったとしても)イギリス発の「エタニティ」パズルのように、私が夢中になれるタイプのパズルです。
追伸:イギリスではなぜ「colour」を「au」で綴るのでしょうか?私には全く意味が分かりません。
「ザ・プライス・イズ・ライト」の「パンチ・ア・バンチ」ゲームにおけるパンチ1回あたりの平均賞金と最適な戦略は何ですか?
ルールを知らない方は、ザ・プライス・イズ・ライトのウェブサイトで説明されています。ルールはご存知だと仮定しているので、もしこのゲームを知らない方は、ぜひウェブサイトをご覧ください。YouTubeにもこのゲームの動画がいくつかあります。こちらは昔の動画です。セカンドチャンスの動画ですが、当時の最高賞金は1万ドルでした。現在は2万5千ドルです。
まず、セカンドチャンスが付かない賞品の期待値を計算してみましょう。次の表は、平均が1371.74ドルであることを示しています。
二度目のチャンスなしのパンチ・ア・バンチ賞品配布
| 賞 | 番号 | 確率 | 予想される勝利 |
| 25000 | 1 | 0.021739 | 543.478261 |
| 10000 | 1 | 0.021739 | 217.391304 |
| 5000 | 3 | 0.065217 | 326.086957 |
| 1000 | 5 | 0.108696 | 108.695652 |
| 500 | 9 | 0.195652 | 97.826087 |
| 250 | 9 | 0.195652 | 48.913043 |
| 100 | 9 | 0.195652 | 19.565217 |
| 50 | 9 | 0.195652 | 9.782609 |
| 合計 | 46 | 1.000000 | 1371.739130 |
次に、2回目の当選確率がある当選金の平均額を計算します。次の表は、平均額が225ドルであることを示しています。
セカンドチャンスでパンチ・ア・バンチ賞品配布
| 賞 | 番号 | 確率 | 予想される勝利 |
| 500 | 1 | 0.250000 | 125.000000 |
| 250 | 1 | 0.250000 | 62.500000 |
| 100 | 1 | 0.250000 | 25.000000 |
| 50 | 1 | 0.250000 | 12.500000 |
| 合計 | 4 | 1.000000 | 225.000000 |
3つ目に、プレイヤーが2回チャンスを得る確率に基づいて期待値表を作成します。これは簡単な計算で求めることができます。例えば、2回チャンスを得る確率は(4/50)×(3/49)×(46/48)です。s回チャンスを得た場合の期待値賞金は$1371.74 + $s×$225です。次の表は、0回から4回チャンスを得た場合の確率と平均賞金を示しています。
パンチ・ア・バンチ賞品返却テーブル
| セカンドチャンス | 確率 | 平均勝利 | 予想される勝利 |
| 4 | 0.000004 | 2271.739130 | 0.009864 |
| 3 | 0.000200 | 2046.739130 | 0.408815 |
| 2 | 0.004694 | 1821.739130 | 8.551020 |
| 1 | 0.075102 | 1596.739130 | 119.918367 |
| 0 | 0.920000 | 1371.739130 | 1262.000000 |
| 合計 | 1.000000 | 1390.888067 |
したがって、パンチ 1 回あたりの平均勝ち額 (2 回目のチャンスによる追加金額を含む) は 1,390.89 ドルになります。
以下の表は、残りパンチ数に応じて、最低限の勝利金を受け入れるための私の戦略を示しています。プレイヤーは、3回のセカンドチャンスで$1,000 + $250、$100 + $50の賞金を獲得し、$1,400まで到達できることに注意してください。
パンチ・ア・バンチ戦略
| 残りパンチ | 最低限のスタンド |
| 3 | 5,000ドル |
| 2 | 5,000ドル |
| 1 | 1,400ドル |
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
答えがわからない場合、ゲーム番組「ミリオン ダラー マネー ドロップ」でお金を分配するための最適な戦略は何でしょうか?
他の読者のために、まずルールを確認したいと思います。
- プレーヤーのチームは 1,000,000 ドルからスタートします。
- チームには多肢選択式の質問が与えられます。
- チームは賭けたお金を選択肢の中から選んだ答えに分配します。正解に賭けた金額が次の質問に進みます。
- チームは、少なくとも 1 つの可能性のある答えにお金を賭けないことで、その答えを完全に排除する必要があります。
- このプロセスは数ラウンドにわたって繰り返されます。プレイヤーには考えを変えるチャンスが1回与えられます。
当然のことながら、チームが答えを確信しているなら、彼は全財産を正解に賭けるべきです。もしチームが答えを2つに絞り込み、それぞれの正解確率を50%とした場合、彼は賭け金を2つの選択肢に均等に分配すべきです。
チームが一つの答えに傾きながらも、他の選択肢を完全に排除していない場合、状況はさらに難しくなります。例を見てみましょう。チームがそれぞれの正解の確率を次のように算出したとします。A 10%、B 20%、C 30%、D 40%。賞金はどのように分配すべきでしょうか?
答えはケリー基準に従うことだと私は主張します。簡単に言うと、チームは質問ごとに彼の資産の対数を最大化する必要があります。そのためには、既にどれだけの資産を持っているかを考慮する必要があります。
番組とは関係なくあなたが既に蓄えた資産が10万ドルだとしましょう。これが最初の質問なので、ゲーム番組の賞金100万ドルを分配する必要があります。まず、番組のルールに従い、最も確率の低い選択肢を除外します。次に、0.2×log(100,000+b×1,000,000) + 0.3×log(100,000+c×1,000,000) + 0.4×log(100,000+d×1,000,000)を最大化します。ここで、小文字のa、b、cはそれぞれの回答に割り当てられる割合を表します。
これは微積分を使って三項方程式を解いたり、試行錯誤したり、あるいは私の好みであるExcelの「ゴールシーク」機能を使って解くことができます。どれを使うにせよ、正解はBに18.9%、Cに33.3%、Dに47.8%を当てはめることです。
もちろん、番組出演者全員が制限時間内にこれだけの計算をこなせるわけではありません。ましてや、その時間内に大量の現金を移動させなければならないのは言うまでもありません。より現実的なアドバイスとしては、最も可能性の低い選択肢はあり得ないと仮定し、正解の確率に応じてお金を分配することです。この例では、Bに22.2%、Cに33.3%、Dに44.4%という割合になります。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
ミシガン州宝くじには、次のルールの 3 人用ゲームがあります。 このゲームで後攻に有利なポジションはありますか?各プレイヤーにとって最適な戦略は何でしょうか? このゲームの様子を映したYouTube動画をご覧ください。
まず、最後にプレイしても位置的な有利性はありません。前のプレイヤーがプレイしている間、プレイヤーは防音ブース内にいるので、順番は関係ありません。
第二に、ゲームにはナッシュ均衡が存在し、少なくともx点のスコアで勝利する戦略が他のどの戦略よりも優れている必要があります。問題はx点を見つけることです。
私がしたのは、1から100までの番号が書かれたカードの代わりに、各プレイヤーが0から1までの一様分布の乱数を受け取り、完璧な論理学者がスタンドとスイッチのどちらにも無差別となる点xを探すという戦略を立てることです。この答えがあれば、1から100までの離散分布に簡単に適用できます。
ここまでで話は終わりにして、読者の皆さんに問題を解いてもらいます。答えと解答については、以下のリンクをご覧ください。
0 から 1 までの連続分布の答え。
1 から 100 までの離散分布に対する回答。
私の解決策については、ここをクリックしてください(PDF) 。
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されました。
何の価格についても知識がないと仮定した場合、「ザ・プライス・イズ・ライト」のレースゲームに最適な戦略は何でしょうか?
ルールを知らない方のために説明すると、プレイヤーは4枚の値札を受け取り、4つのアイテムにそれぞれ値札を貼らなければなりません。貼り終えたらレバーを引くと、正解の数が分かります。正解が4枚に満たない場合は、値札を並び替えて再挑戦できます。45秒以内であれば、何度でも挑戦できます。
過去の選出履歴とスコアを踏まえ、常に受賞の可能性があるものを選出して提出することをお勧めします。最初のスコアが0の場合は、2つのタグを2セット反転させるのではなく、どちらかの方向に1つずつ順位を移動させてください。
その場でロジックが理解できない場合は、以下に説明を記載します。この戦略を使うには、各タグにA、B、C、Dの文字を割り当てます。そして、ステージ上の左から右へ、表示されている順番に配置します。必ずABCDから始めてください。次に、以下のスコア履歴を確認し、そのスコアシーケンスに示されているタグの順番を選択してください。
0の場合、BCDA
0-0の場合はCDAB
0-0-0の場合はDABC(必ず勝つ)
0-1の場合はBDAC
0-1-0の場合はCADB(必ず勝つ)
0-1-1の場合、CDBA
0-1-1-0の場合はDCAB(必ず勝つ)
0-2の場合はBADC
0-2-0の場合はDCBA(必ず勝つ)
1の場合、ACDB
1-0の場合はBDCA
1-0-0の場合はCABD
1-0-0-1の場合はCBAC(必ず勝つ)
1-1の場合はBDCA
1-1-0の場合はCABD
1-1-0-1の場合はCBAC(必ず勝つ)
1-1-1の場合はBCAD(必ず勝つ)
2の場合、ABDC
2-0の場合はBACD(必ず勝つ)
2-1の場合はACBD
2-1-0の場合はDBCA
2-1-1の場合はADCB
2-1-1-0の場合はCBAD(必ず勝つ)
以下の表は、各ターン数における確率を示しています。右下のセルは、期待されるターン数が10/3であることを示しています。
レースゲーム
| ターン | 組み合わせ | 確率 | 戻る |
|---|---|---|---|
| 1 | 1 | 0.041667 | 0.041667 |
| 2 | 4 | 0.166667 | 0.333333 |
| 3 | 8 | 0.333333 | 1.000000 |
| 4 | 8 | 0.333333 | 1.333333 |
| 5 | 3 | 0.125000 | 0.625000 |
| 合計 | 24 | 1.000000 | 3.333333 |
この質問はWizard of Vegasの私のフォーラムで議論されています。
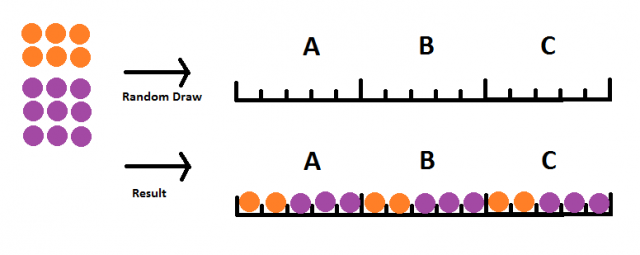
Price is Right の Showcase Showdown で特定のプレイヤーが 25,000 ドルを獲得する確率はどれくらいですか?
他の読者への説明として、あなたが何を言っているのか説明させてください。ショーケース・ショーダウンは、ゲーム番組「ザ・プライス・イズ・ライト」で行われるゲームです。ショーケース・ショーダウンでは、各プレイヤーが順番にホイールを回し、0.05 から 1.00 まで、0.05 で割り切れるすべての金額で止まる確率が等しくなります。プレイヤーが最初のスピンが気に入らなかった場合は、2 回目のスピンを 1 回目に加えてもう一度スピンできますが、1.00 を超えると即座に失格となります。同点の場合は、各プレイヤーはタイブレーカー ラウンドで 1 回スピンし、最も高いスピンを行ったプレイヤーが勝ちます。再度同点の場合は、同点が解消されるまでこのプロセスが繰り返されます。
ショーケース・ショーダウンの主な目的は、ショーケースへの進出です。ただし、以下の通り、賞金も即時獲得可能です。
- 最初のラウンドで、プレイヤーが 1 回の合計または 2 回のスピンの合計で合計 $1.00 を獲得した場合、そのプレイヤーは $1,000 を獲得します。
- 最初の、そして唯一の最初のタイブレーカー ラウンドで、ホイールが $0.05 または $0.15 に止まった場合、プレイヤーは $10,000 を獲得します。
- 最初の、そして唯一の最初のタイブレーカー ラウンドで、ホイールが 1.00 ドルに止まった場合、プレイヤーは 25,000 ドルを獲得します。
コラム#101では、ショーケース・ショーダウンに最適な戦略について解説しました。この戦略を前提として、以下の表は皆様の疑問やその他の様々な点にお答えします。
ショーケース対決統計
| 質問 | 答え |
|---|---|
| 第1ラウンドの予想賞金1000ドルの勝者 | 0.253790 |
| 2人同点の確率 | 0.113854 |
| 3人同点の確率 | 0.004787 |
| 第2ラウンドで予想される賞金10,000ドルの勝者 | 0.024207 |
| 第2ラウンドの優勝者予想賞金25,000ドル | 0.012104 |
| 予想賞金総額 | 798.45ドル |
| 特定のプレイヤーが1000ドルを獲得する確率 | 0.084597 |
| 特定のプレイヤーが10000ドルを獲得する確率 | 0.008069 |
| 特定のプレイヤーが25000ドルを獲得する確率 | 0.004035 |
表の一番下の行は、スピンの順番を考慮せずにショーケース ショーダウンに参加した場合、25,000 ドルを獲得する確率が 0.004035、つまり 248 分の 1 であることを示しています。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
ゲーム番組「サバイバー」では、9人チームと6人チームの2つのチームがありました。その後、参加者はランダムに5人ずつの3つの新チームに振り分けられました。各新チームは、元の9人チームから3人、元の6人チームから2人で構成されていました。この確率はどれくらいでしょうか?
9人だったチームをチーム1、6人だったチームをチーム2としましょう。チーム1から3人、チーム2から2人を選ぶ方法はcombin(9,3)×combin(6,2) = 1,260通りです。15人中5人を選ぶ方法はcombin(15,5) = 3,003通りです。つまり、最初のチームが3/2でチーム1に有利になる確率は1,260/3,003 = 41.96%です。
そうなった場合、チーム1は6人、チーム2は4人の選手が残ります。チーム1から3人、チーム2から2人を選ぶ場合の選択肢は、combin(6,3)×combin(4,2) = 120通りです。残りの10人のうち5人を選ぶ場合の選択肢は、combin(10,5) = 252通りです。つまり、チーム1が既に3/2で優勢になっている場合、チーム2がチーム1に有利な3/2で優勢になる確率は、120/252 = 47.62%となります。
最初の 2 つの新しいチームが、以前のチーム 1 を優先して 3/2 に分割された場合、最後のチームは残りのチーム間で 3/2 に分割されます。
したがって、質問の答えは 41.96% × 47.62% × 100% = 19.98% となります。
数式:
組み合わせ(x,y)=x!/((y!*(xy)!)
x! = 1*2*3*...*x
この質問は、 Wizard of Vegasの私のフォーラムで提起され、議論されています。
ジェームズ・ホルツハウアーは、前回のエマ戦でわざと負けたのだと思います。私の証拠は、それまで毎回高額を賭けていたのに、エマ戦では突然低額に賭けたということです。プロデューサーは、アレックスが降板した後、ケン・ジェニングスに司会を任せたいと思っているのではないでしょうか。司会者が両方の番組で記録と賞金を握っていたら、番組はもっとドラマチックになるでしょう。そこで、ジェームズに金を支払って試合を放棄させたのです。
状況を説明しましょう。2019年6月3日、ジェームズは通常ゲームで獲得した賞金総額の記録をあと少しで破るところまで来ていました。その記録は現在も破られていませんが、1ゲームあたりの平均獲得賞金は記録破りに必要な金額をはるかに上回っていました。そのため、6月3日には誰もが記録更新に注目していました。
ところが、ジェームズは記録を破ることができず、負けてしまいました。勝者のエマは、ブザーの使い方が上手で、ただ正しく答えるだけでなく、非常に戦略的なゲームを展開しました。彼女はいつものジェームズと同じようにプレイしました。最終ジェパディのスコアは以下のとおりです。
- エマ — 26,600ドル
- ジェームズ — 23,400ドル
- ジェイ — 11,000ドル
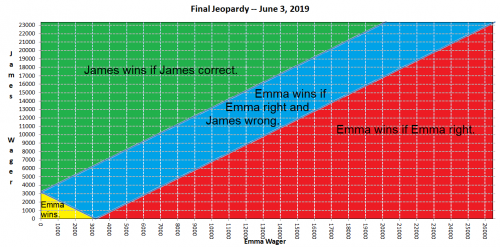
2位が1位の半分以上のスコアを持ち、3位がそうでない状況では、通常、1位と2位が最終賭け金を高くするか低くするかで勝負が決まります。1位に高く賭ければ、正しく賭ければ勝利が確定します。具体的には、2位のスコアの2倍から1位のスコアを差し引いた金額に1ドルを加算した金額です。エマはまさにこの賭け方で、2×23,400ドル - 26,600ドル + 1ドル = 20,201ドルを賭けました。多くの場合、1位のプレイヤーはこのように賭けます。
しかし、ジェームズは賭けを決める際にエマがどうするかを知りませんでした。次の表は、賭けの組み合わせによって誰が勝つかを示しています。
エマが少なくとも 20,201 ドルを賭けた場合、正解すれば勝利が確定します。
エマが低額を賭けた場合、(a) ジェームズが低額を賭けるか、(b) ジェームズが高額を賭けて間違っているかのいずれかであれば、エマが勝ちます。
ジェームズが高額を賭けた場合、(a) エマが高額を賭け、エマが間違っていて、ジェームズが正しいか、(b) エマが低額を賭け、ジェームズが正しいかのどちらかであれば、ジェームズの勝ちとなります。
ジェームズが低い賭け金をした場合、エマが高い賭け金を出して間違っていれば、ジェームズが勝ちます。
もし完璧な論理学者同士が対戦していたら、両者ともランダムに判断を下すでしょう。しかし、このような状況でリーダーがロースコアを取れることは稀です。ジェームズがエマがハイスコアを取ると予想したなら、彼は絶対にロースコアを取るべきです。そうすれば、ジェームズはファイナルジェパディで正解しなくても勝つことができ、エマが失敗することを期待するだけで済みます。
ジェイが全額を賭けて正しかった場合、ジェームズの実際の入札額はジェイをカバーするのに適切な額でした: $23,400 - 2 × $11,000 - $1 = $1,399。これは、エマに勝つための低額賭け金として満足のいく額でした。
これが正しいとすると、ジェームズは3位に比べて2位になったことで1,000ドル多く受け取ることになる。
結論として、ジェームズが試合を放棄したという陰謀論を完全に否定します。彼は正しいプレーをしていたにもかかわらず、強豪との対戦と、多くの人が「不運」と呼ぶような要因が重なって負けたのです。
外部リンク
- ジェパディ殿堂
- Jeopardy の James Holzhauer — Wizard of Vegas の私のフォーラムでの議論。
Final Jeopardyで、2位のプレイヤーが1位のプレイヤーの2/3以上の賞金を持っている場合、最適な戦略は何ですか?3位のプレイヤーは考慮しないと仮定します。
まず最初に免責事項を述べさせてください。以下の分析は統計的な平均値に基づいています。実際にプレイする方は、Final Jeopardyのカテゴリーをどれだけ熟知しているか、そして対戦相手の正解率を推測するなど、精神的な調整を行う必要があります。
あなたの質問に答えるために、私はまず、 Jeopardy アーカイブの 4 シーズン分のデータを調べ、1 位 (リード) と 2 位 (追随) のプレイヤーが Final Jeopardy に正解した場合と不正解した場合の 4 つの可能な組み合わせを確認しました。
最終ジェパディスコアカード
| リーディングプレーヤー | チェイスプレイヤー正解 | 追跡プレイヤーが正しくありません | 合計 |
|---|---|---|---|
| 正しい | 29.0% | 25.5% | 54.5% |
| 正しくない | 17.7% | 27.8% | 45.5% |
| 合計 | 46.8% | 53.2% | 100.0% |
先に進む前に、いくつかの変数を定義しましょう。
x = リードしているプレイヤーが上位に行く確率。
y = 追いかけるプレイヤーが上がる確率。
f(x,y) = 高いプレイヤーが勝つ確率。
上の表から、f(x,y) を x と y で表してみましょう。
f(x,y) = 0.823xy + 0.545x(1-y) + 0.468(1-x)y + (1-x)(1-y)
f(x,y) = 0.810 xy - 0.455x - 0.532y + 1
x と y の最適値を見つけるには、x と y の両方に関して f(x,y) の微分をとります。
f(x,y) d/dx = -0.455 + 0.810y = 0
したがって、y = 0.455/0.810 = 0.562
f(x,y) d/dy = -0.532 + 0.810x = 0
したがってx = 0.523/0.810 = 0.657
したがって、ハイプレイヤーは 65.7% の確率でハイに賭けるべきであり、ロープレイヤーは 56.2% の確率でハイに賭けるべきです。
観察した結果、ハイプレイヤーは65.7%以上の確率でハイを賭けていると思うので、もし私が2位だったらローを賭けるでしょう。
両方のプレイヤーがこのランダム化戦略に従う場合、リードしているプレイヤーが勝つ確率は 70.1% です。
理論はさておき、リードしているなら、追っているプレイヤーの行動を予測し、同じ行動を取りましょう。逆に、追っているなら、リードしているプレイヤーの行動を予測し、その逆の行動を取りましょう。この戦略は、あらゆるトーナメントに当てはまります。この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。
ジェパディのラウンド開始時、ジェームズ・ホルツハウアーのようなプレイヤーが下から順に答えを選ぶのはなぜでしょうか? 難しい場合もあるカテゴリーを正しく理解するためにも、簡単な問題からウォーミングアップしていく方が理にかなっているのではないでしょうか?
その理由は、デイリーダブルが91.5%の確率で下3列に配置されるからです。以下の表は、13,660個のデイリーダブルが見つかった場合のボード上の位置を示しています。
デイリーダブルロケーション
| 行 | コラム1 | コラム2 | コラム3 | コラム4 | コラム5 | コラム6 | |
|---|---|---|---|---|---|---|---|
| 1 | 5 | - | 3 | 3 | 2 | 3 | 16 |
| 2 | 280 | 137 | 216 | 167 | 207 | 140 | 1,147 |
| 3 | 820 | 442 | 677 | 658 | 643 | 472 | 3,712 |
| 4 | 1,095 | 659 | 982 | 907 | 895 | 627 | 5,165 |
| 5 | 787 | 403 | 670 | 671 | 613 | 476 | 3,620 |
| 合計 | 2,987 | 1,641 | 2,548 | 2,406 | 2,360 | 1,718 | 13,660 |
出典: J!アーカイブ。
以下は、ボードの各セルにデイリーダブルがどのくらいの頻度で出現したかを示す同じデータです。
毎日のダブル確率
| 行 | コラム1 | コラム2 | コラム3 | コラム4 | コラム5 | コラム6 | |
|---|---|---|---|---|---|---|---|
| 1 | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.1% |
| 2 | 2.0% | 1.0% | 1.6% | 1.2% | 1.5% | 1.0% | 8.4% |
| 3 | 6.0% | 3.2% | 5.0% | 4.8% | 4.7% | 3.5% | 27.2% |
| 4 | 8.0% | 4.8% | 7.2% | 6.6% | 6.6% | 4.6% | 37.8% |
| 5 | 5.8% | 3.0% | 4.9% | 4.9% | 4.5% | 3.5% | 26.5% |
| 合計 | 21.9% | 12.0% | 18.7% | 17.6% | 17.3% | 12.6% | 100.0% |
デイリーダブルを探す理由は、スコアを2倍にする良い方法だからです。ほとんどの参加者は、与えられたヒントを正解する確率が80%から90%程度です。勝率80%から90%の賭け金で、配当が均等になるというのは非常に価値があります。ジェームズ・ホルツハウアーがこれほどの勝率を上げた主な理由は、積極的にデイリーダブルを探し、見つけたらほとんどの場合「オールイン」したことです。また、エマも同じ戦略で彼に対して負けました。
プレイヤーが賞品の価格を全く知らないと仮定して、「プライス・イズ・ライト」のレースゲームをプレイするための最善の戦略は何ですか?
このゲームを知らない読者のために、ビデオを掲載します。
以下の戦略は、平均ターン数が最小となると考えています。これと同等の戦略は数多くありますが、これを上回る戦略はないと思います。
この戦略を使うには、4 つの値札に 1、2、3、4 とラベルを付けます。最初に左から始めて、過去に何回正解したかの履歴に従って、4 つの賞品に値札を付けます。
レースゲーム戦略
| 歴史 | 賞品1 | 賞品2 | 賞品3 | 賞品4 |
|---|---|---|---|---|
| なし | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0,2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
次の表は、4 つの値札を並べる 24 通りの方法のうち、1 ~ 5 ターンかかる確率を示しています。
必要なターン数
| ターン | 番号 | 確率 |
|---|---|---|
| 1 | 1 | 4.17% |
| 2 | 4 | 16.67% |
| 3 | 8 | 33.33% |
| 4 | 9 | 37.50% |
| 5 | 2 | 8.33% |
| 合計 | 24 | 100.00% |
ドット積を取ると、この戦略で必要な平均ターン数は 3.29167 になります。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
Final Jeopardyの賭け金には3分の2ルールがあるって聞いたんだけど、知ってる?
はい。2位プレイヤーのスコアが1位プレイヤーの2/3以上になった場合、2位プレイヤーの戦略変更を指します。
次のように、状況を 2 人用ゲームに単純化してみましょう。
- 状況 A: 2 位の人数が 1 位の人数の半分未満である。
- 状況 B: 2 番目のプレイヤーが 1 位の 1/2 から 2/3 の権利を持っています。
- 状況C: 2位の順位が1位の順位の2/3以上である。
話を進める前に、読者の皆様に「ファイナル・ジェパディ」後の同点に関するジェパディのルール変更について改めてお伝えしておきます。両プレイヤーが進出することはなくなり、サドンデス方式のタイブレーカー問題が導入されました。例えば、以下のような状況です。
状況A
A=10,000ドル、B=4,000ドルとします
プレイヤーAは、A-2B-1以上の賭け金を賭けて負けるリスクを負うべきではありません。もしこのカテゴリーに自信がない場合は、$0を賭けることもできます。いずれにしても、Aは確実に勝利します。この場合、Aは$0から$1,999の間で賭けるべきです。
プレイヤーBは、Aが賭けすぎて外れない限り、望みはありません。ここでBは3位のスコアを考慮し、できれば3位のスコアを上回るように努めるべきです。3位で1,000ドルではなく、2位で2,000ドルを獲得するのです。
状況B
A=10,000ドル、B=6,000ドルとします
Aの戦略は、Bが全額を賭けると予想し、正解の場合は2Bをカバーするのに十分な額を賭けることです。しかし、安全のために、不正解の場合にBを下回るほどの額を賭けるべきではありません。この場合、少なくとも2B-A+1とAB-1を賭けるべきです。この場合、賭ける金額の範囲は$2,001から$3,999です。
Bの戦略は、正解すれば少なくともAを抜くだけの得点を獲得し、全体の得点を上げることです。この場合、4,001ドルと6,000ドルです。
両プレイヤーが予想通りにこの戦略に従った場合、プレイヤーBが勝てる唯一の方法は、Aが間違っていてBが正しい場合です。その確率は約19%です。
状況C
ここでは状況がより複雑になり、より多くのゲーム理論とランダム化が関与することになります。
A=10,000ドル、B=7,000ドルとします。
先に進む前に、Final Jeopardyのヒントが正解する確率を推定することが重要です。シーズン30から34までのデータに基づくと、1位のプレイヤーは52%、2位のプレイヤーは46%の確率で正解しました。しかし、これらの確率は正の相関関係にあります。4つの可能性の内訳は以下のとおりです。
- 両方正解: 27%
- 1位正解、2位不正解:25%
- 1位は不正解、2位は正解: 19%
- 両方とも29%間違っています。
最初の 2 人のプレイヤーの Jeopardy 平均は 49% ですが、両方が正解、または両方が間違っている確率は 56% です。
もちろん、これらはカテゴリに応じて変わる可能性がありますが、ここでは単純に上記の確率を使用しましょう。
この状況では、プレイヤーBはAが間違っていてBが正しいという前提に頼る必要はありません。例えば0ドルといった低額を賭けることで、Aが間違っていたとしても確実に勝ちを確保できます。つまり、AがBをカバーできる額を賭けた場合、もしAが間違っていたとしてもBを下回るリスクを負い、Bが0ドルを賭けたとします。
しかし、AがBが例えば$0という低い賭け金をすると予測した場合、Aも$0を賭けることで勝利を確定できます。基本的に、どちらのプレイヤーも低い賭け金を賭けるか高い賭け金を賭けるかの選択を迫られます。AはBと同じ賭け方を望み、BはBとは逆の賭け方を望むはずです。もし両プレイヤーが完璧な論理的思考力を持つなら、彼らはランダムに決定を下すでしょう。
この場合、Aのハイベットは状況Bと同様に、2B-A+1からAB-1になります。この場合、2,999ドルと4,001ドルになります。Aのローベットは0ドルになります。
Bのハイベットは状況Bの場合と同じで、Aが正解した場合にはパスするのに十分な額を賭けます。この場合、$3,001と$7,000です。Bのローベットは$0です。
数学を省略して、両プレイヤーのランダム化戦略に直接進むことをお許しください。
プレイヤー A は、62.3% の確率でハイを選択し、37.7% の確率でローを選択するはずです。
プレイヤー B は、確率 61.2% で高くなり、確率 38.8% で低くなるはずです。
両方のプレイヤーがこのランダム化戦略に従い、上記の確率の組み合わせが正しいと仮定すると、プレイヤー A が勝つ確率は 65.2% になります。
プレイヤー A のスコアがプレイヤー B の 2/3 以上だった場合、プレイヤー A の勝利確率は 81.0% に上がります。
ダブル ジェパディに賭ける場合、両方のプレイヤーは 2/3 ルールの重要性を念頭に置く必要があります。