このページ
ブラックジャックでデッキの数が重要な理由
概要
ブラックジャックに関する信頼できる情報源は、他の条件が同じであれば、ブラックジャックで使用されるカードのデッキ数とハウスエッジの間には正の相関関係があると必ず述べています。つまり、デッキ数が少ないほど、レクリエーショナルプレイヤーにとってオッズが有利になるということです。これは、少なくともルールの良いゲームを探し回れるだけの知識を持つブラックジャックプレイヤーの間では常識です。しかし、なぜこれが真実なのかを深く掘り下げた解説は見たことがありません。この記事の目的は、この疑問に光を当てることです。
始める前に、いくつかの基本的なルールを設定させてください。これらは、2020年にこの記事を執筆した時点のブラックジャックの状況を考慮して、可能な限り現実的なものになるように選ばれました。
- ディーラーはソフト17をヒットします。
- ブラックジャックは3対2で支払います。
- ディーラーは 10 またはエースが出たらブラックジャックを覗きます。
- プレイヤーは任意の 2 枚のカードをダブルすることができます。
- プレイヤーは降伏できません。
- プレイヤーはスプリット後にダブルすることができます。
- プレイヤーは、ペア(エースを含む)を最大 3 回まで再分割できます。
- 連続シャッフル機を使用します(各ハンドの後にカードがシャッフルされます)。
- プレイヤーは基本戦略を使用します。
私のブラックジャックのハウス エッジ計算機によると、これらのルールでは、デッキの数に応じてハウス エッジは次のようになります。
ブラックジャックのハウスエッジ(Decks別)
| デッキ | ハウスエッジ |
|---|---|
| 1 | 0.014% |
| 2 | 0.341% |
| 4 | 0.499% |
| 6 | 0.551% |
| 8 | 0.577% |
これらの数値は、ブラックジャックに関する他の信頼できる情報源と完全に一致しない可能性があります。差異は、カットカードが使用されているか、プレイヤーが最適な構成依存戦略を採用していることによるものと考えています。比較対象として、私は毎ハンド後にカードがシャッフルされ、プレイヤーは常に合計依存の基本戦略に従うと仮定しています。
8デッキと1デッキのハウスエッジの差は0.563%であることにご注目ください。この記事では、デッキ数がなぜオッズにこれほど大きな影響を与えるのかという疑問に答えていきます。
バランスの取れたゲーム
まず、プレイヤーとディーラーのルールが全く同じで、デッキの数に関わらずハウスエッジが0%となる、簡略化されたブラックジャックゲームを考えます。次に、実際のブラックジャックのルールを一つずつ追加し、デッキの数によってハウスエッジがどのように変化するかを調べます。
最初の仮想的な簡易ブラックジャック ゲームは、次の点を除いて、前述のルールと同じになります。
- プレイヤーは「ディーラーを模倣する」戦略に従います。
- ブラックジャックで勝つと、同額のお金が支払われます。
- プレイヤーとディーラーの両方がバストした場合、結果はプッシュになります。
このバランスの取れたゲームでは、すべてのルールが両方向に均等に適用されるため、ハウス エッジは明らかに 0.000% になります。
ディーラーのポジショナルアドバンテージ
ブラックジャックでプレイヤーとディーラーの両方がバストした場合、どちらが勝つのでしょうか?ディーラーです。言い換えれば、ディーラーはポジション上の優位性を得ています。先にバストした方が負け、プレイヤーが先にアクションを取らなければならないからです。これが、プレイヤーの利益を削る多くのルールがあるにもかかわらず、ディーラーが有利である理由です。このルールをバランスゲームに追加し、1デッキと8デッキのシミュレーションを実行すると、プレイヤーの期待リターンは以下のようになります。
ルール変更による期待値
| ルール | 1つのデッキ | 8つのデッキ | 違い |
|---|---|---|---|
| ディーラーの位置的優位性 | -8.237% | -8.157% | -0.079% |
上の表は、この仮想ゲームにおいて、1デッキの場合と8デッキの場合を比較すると、プレイヤーのオッズが悪くなることを示しています。これは、デッキの数が少なくなるにつれて、バーストする確率が上昇するためです。以下は、この「ディーラーを真似る」ゲームで、プレイヤーが先にバストしたとしてもディーラーが手札を全てプレイすると仮定した場合のバスト確率です。
- 1デッキ = 27.333%
- 8デッキ = 27.209%
上記の結果から、1デッキのゲームでは、8デッキのゲームと比較して、どちらかの側がバストする確率が0.124%高いことがわかります。それぞれの側のバストにはある程度の相関関係があるため、プレイヤーとディーラーがバストする4つの組み合わせすべてを見てみましょう。
破産確率
| プレイヤーバスト | ディーラーの破産 | 1つのデッキ | 8つのデッキ | 違い |
|---|---|---|---|---|
| いいえ | いいえ | 44.096% | 44.468% | -0.372% |
| いいえ | はい | 19.095% | 19.051% | 0.044% |
| はい | いいえ | 19.095% | 19.051% | 0.044% |
| はい | はい | 8.237% | 8.157% | 0.079% |
| 合計 | 90.524% | 90.728% | -0.204% |
確率の合計が 100% にならない理由は、どちらかの側がブラックジャックを持っていて、それ以外ではハンドがプレイされないハンドがテーブルでカウントされないためです。「はいはい」の行は、両方がバストし、ディーラーの勝ちとなる状況を示しています。これは、8 デッキのゲームと比較して、シングル デッキのゲームでこれが発生する頻度が 0.080% 多いことを示しています。なぜでしょうか。どちらかの側がバストした場合は、12 ~ 16 ポイントのハード ハンドをヒットした後である必要があります。このハンドは、少なくとも 2 枚のカードで構成されていなければなりません。一方、どちらかの側が 2 枚の高価値カードを持っていた場合は、スタンドします。言い換えれば、ヒットは通常、平均価値よりも小さいカードを持つハンドで発生します。ヒットする状況でこの小さなカードを除去すると、残りのカードに高価値カードが余剰になります。バストの前に小さなカードを除去するこの効果は、シングル デッキのゲームでより顕著になります。
ブラックジャックは3対2で配当する
バランスゲームに追加する次のルールは、ブラックジャックに勝ったプレイヤーが 3 対 2 を支払うというものです。このルールをシミュレーションに追加すると、プレイヤーの累積予想収益は次のようになります。
- 1デッキ = -5.912%
- 8デッキ = -5.894%
このルールを追加するための行が追加されたシミュレーション結果テーブルは次のようになります。
ルール変更による期待値
| ルール | 1つのデッキ | 8つのデッキ | 違い |
|---|---|---|---|
| ディーラーの位置的優位性 | -8.237% | -8.157% | -0.079% |
| ブラックジャックで勝ったプレイヤーは3対2で配当される | -5.912% | -5.894% | -0.018% |
2 行の差をとると、ブラックジャックで勝った場合のプレイヤーの利益が 3 対 2 で支払われることがわかります。
- 1デッキ = 2.325%
- 8デッキ = 2.263%
- 差 = 0.062%
これは数学的に簡単に検証できます。dはデッキの数です。Excelの表記法を用いると、ブラックジャックで勝つ確率は、確率(プレイヤーのブラックジャック) * (1-確率(ディーラーのブラックジャック)) = (16*d)*(4*d)/combin(52*d,2) * [1-(16*d-1)*(4*d-1)/combin(52*d-2,2) となります。
ブラックジャックの勝率
| デッキ | 確率 |
|---|---|
| 1 | 4.649% |
| 2 | 4.578% |
| 4 | 4.544% |
| 6 | 4.532% |
| 8 | 4.527% |
上で見たように、ブラックジャックの勝つ確率はデッキ数が減るほど高くなります。これは単に除去の効果によるものです。たとえば、最初のプレイヤー カードが 10 の価値を持つカードだとします。この確率は、デッキ数に関係なく 4/13 です。シングル デッキのゲームでは、2 枚目のカードがエースである確率は 4/51 = 7.843% であることが簡単にわかります。8 デッキのゲームでは、その確率は 32/415 = 7.711% となり、シングル デッキのゲームよりも 0.123% 低くなります。簡単に言うと、シングル デッキのゲームでエースを得る確率が高い理由は、デッキから 10 を除いた後、デッキにエースが多くなるためです。最初のカードがエースの場合も同じで、シングル デッキのゲームでは残りのカードに 10 が多くなります。
さらに、プレイヤーがブラックジャックになった場合、ディーラーがブラックジャックになる確率はデッキ数が減るにつれて低下します。これは、シングルデッキのゲームではプレイヤーがデッキからエースと10を取り除くため、8デッキのゲームに比べてディーラーがブラックジャックになるのがはるかに難しくなるためです。具体的には、プレイヤーがすでにブラックジャックを持っていると仮定した場合、ディーラーがブラックジャックになる確率は、1デッキの場合は3.673%、8デッキの場合は4.605%です。プレイヤーはブラックジャックが勝つたびに、追加の0.5ユニットを獲得します。この仮想的なバランスの取れたゲームでブラックジャックが勝つと3-2の配当が得られるという価値を得るには、ブラックジャックが勝つ確率に、その追加の0.5ユニットごとに0.5を掛けます。これにより、デッキ数によるプレイヤーの有利性は次のようになります。
ブラックジャックで勝つことで得られるプレイヤーの優位性
| デッキ | プレイヤーエッジ |
|---|---|
| 1 | 2.325% |
| 2 | 2.289% |
| 4 | 2.272% |
| 6 | 2.266% |
| 8 | 2.263% |
ブラックジャックに勝ったプレイヤーが追加の半ユニットを支払うことで数学的に計算された利益は、シングルデッキと 8 デッキで先に示したシミュレーション結果と一致することに注意してください。
以下の表は、これまでに分析したルールの最新リストと、8 つのデッキと比較したシングル デッキ プレイヤーにとってのそのルールの利点を示しています。
ルールの効果
| ルール | シングルデッキ特典 |
|---|---|
| ディーラーの位置的優位性 | -0.079% |
| ブラックジャックで勝ったプレイヤーは3対2で配当される | 0.062% |
| 合計 | -0.018% |
次に、ハード合計が 12 から 16 の場合にスタンドできることによるプレイヤーのメリットを分析しましょう。この範囲での合計に依存する基本戦略は、次のように、どの数のデッキでも同じです。
- 合計が 12 の場合、ディーラーの 4 ~ 6 に対してスタンドし、それ以外の場合はヒットします。
- 合計が 13 ~ 16 の場合はディーラーが 2 ~ 6 の場合はスタンドし、それ以外の場合はヒットします。
この戦略をシミュレーションに追加すると、プレイヤーの期待収益は次のようになります。
- 1デッキ = -2.209%
- 8デッキ = -2.625%
以下のシミュレーション結果テーブルには、このルールを追加するための行が含まれています。
ルール変更による期待値
| ルール | 1つのデッキ | 8つのデッキ | 違い |
|---|---|---|---|
| ディーラーの位置的優位性 | -8.237% | -8.157% | -0.079% |
| ブラックジャックで勝ったプレイヤーは3対2で配当される | -5.912% | -5.894% | -0.018% |
2 行目と 3 行目の差を取ると、プレイヤーがハード 12 から 16 でスタンドする自由意志を持っていることの影響がわかります。
- 1デッキ = 3.703%
- 8デッキ = 3.270%
- 差 = 0.433%
これら2つの数字の差をとると、このルール変更の影響は、シングルデッキのゲームでは8デッキのゲームよりもプレイヤーにとって0.433%高い価値となることがわかります。これは、一般的な考えに反して、シングルデッキのゲームが8デッキのゲームよりもプレイヤーにとって0.563%高い価値となる理由の大部分を説明しています。
ディーラーがスタンドできないのに、プレイヤーが 12 ~ 16 のスティッフ合計でスタンドした場合に何が起こるかを詳しく見てみましょう。次の表は、プレイヤーがスティッフ合計を少なくすることで、プレイヤーのバストが減り、ディーラーのバストが増え、ディーラーがフェイスオフで負ける回数が増えることによって変化するさまざまなイベントからプレイヤーが得られる利益を示しています。
ハード12~16でスタンドした場合の可能性のある結果
| イベント | 1つのデッキ | 8つのデッキ | 違い |
|---|---|---|---|
| プレイヤーのみの逮捕が減少 | 6.282% | 6.271% | 0.010% |
| ディーラー限定の逮捕が増加 | 4.228% | 4.171% | 0.057% |
| 両方のバストが減少 | 4.228% | 4.172% | 0.055% |
| フェイスオフでの勝利数が少なくなる | -1.914% | -2.039% | 0.125% |
| ディーラーはより多くのフェイスオフに勝つ | -9.121% | -9.306% | 0.185% |
| 合計 | 3.703% | 3.270% | 0.433% |
同じ表は、ディーラーが頻繁にバストし、フェイスオフで負ける回数が増えることで、より多くの勝利が得られるという利点を示すために簡略化されています。
ハード12~16でスタンドした場合の可能な結果のまとめ
| イベント | 1つのデッキ | 8つのデッキ | 違い |
|---|---|---|---|
| プレイヤーバストの利益は減少 | 14.738% | 14.615% | 0.123% |
| フェイスオフでの敗北 | -11.035% | -11.345% | 0.310% |
| 合計 | 3.703% | 3.270% | 0.433% |
分かりやすく言えば、シングルデッキゲームでは、プレイヤーは基本戦略に従い、ハードトータルが12~16の場合、ディーラーよりもバストする確率が14.738%低くなります。しかし、これらのハンドのうち、ディーラーがバストしない確率は75%です。その結果、16以下の勝てないハンドを持つプレイヤーとのフェイスオフでは、ディーラーが勝利します。すべてのハンドと比較すると、プレイヤーはバストが少ないことで14.738%の節約になりますが、フェイスオフでの損失が増えることで11.035%の損失を被るため、シングルデッキゲームでは純利益は3.703%となります。
この利益は8デッキゲームではわずか3.270%です。総合的に考えると、12~16で戦略的にスタンディングすることの利益は、8デッキゲームよりもシングルデッキゲームの方が0.433%高くなります。
1 デッキの場合と 8 デッキの場合で、戦略的なスタンドのほうが価値が高いのはなぜでしょうか。その答えは、シングルデッキ ゲームでディーラーの位置的優位性がより重要である理由と似ています。シングルデッキ ゲームではバーストが多く発生します。バーストの多さは双方にメリットをもたらしますが、両方がブレークするとプレイヤーが負けるため、プレイヤーにとってより不利になります。プレイヤーがスタンドするときの合計が 12 から 16 の場合、大きいカードよりも小さいカードの方が多い可能性があります。そのため、デッキにはプレイヤーをバストさせる可能性のある高いカードが多く残ります。プレイヤーがハンドを強くするために必要なこれらの低いカードを除去することによる影響は、8 デッキの場合よりもシングルデッキ ゲームの方が大きくなります。言い換えると、シングルデッキ ゲームではスティフをヒットすることはより危険です。シングルデッキ ゲームではスタンドする方がより有利です。
各ルール変更のコスト/メリットの最新表は次のとおりです。
ルールの効果
| ルール | シングルデッキ特典 |
|---|---|
| ディーラーの位置的優位性 | -0.079% |
| ブラックジャックで勝ったプレイヤーは3対2で配当される | 0.061% |
| プレイヤーはハード12から16でスタンドできる | 0.433% |
| 合計 | 0.415% |
プレイヤーはダブル
次に、ダブルが認められることによるプレイヤーの利益を分析してみましょう。効果を検証するために、デッキ数に応じた適切なダブル戦略(この記事の後半で紹介)をシミュレーションに採用しました。この戦略をシミュレーションに追加すると、プレイヤーの期待リターンは以下のようになります。
- 1デッキ = -0.556%
- 8デッキ = -1.245%
このシミュレーション結果テーブルには、このルールを追加するための行が含まれています。
ルール変更による期待値
| ルール | 1つのデッキ | 8つのデッキ | 違い |
|---|---|---|---|
| ディーラーの位置的優位性 | -8.237% | -8.157% | -0.079% |
| ブラックジャックで勝ったプレイヤーは3対2で配当される | -5.912% | -5.894% | -0.018% |
| プレイヤーはハード12から16でスタンドできる | -2.209% | -2.625% | 0.415% |
| プレイヤーはダブルできる | -0.556% | -1.245% | 0.689% |
3 行目と 4 行目の違いは、次のように、プレイヤーが倍増する自由意志を持っていることによる影響を示しています。
- 1デッキ = 1.653%
- 8デッキ = 1.380%
- 差 = 0.273%
これら2つの数字の差をとると、このルール変更の影響は、シングルデッキのゲームでは8デッキのゲームよりもプレイヤーにとって0.273%高いことがわかります。これは、シングルデッキのゲームが8デッキのゲームよりもプレイヤーにとって0.563%高い価値を持つ理由のもう1つの重要な部分を説明しています。
なぜシングルデッキのゲームではダブルがより価値があるのでしょうか?プレイヤーがダブルを行う場合、ほとんどの場合、9~11点のハード合計点の時です。ダブルは2枚のカードで行うため、9~11点の低い合計点数にするには、平均よりも小さい2枚のカードが必要になります。シングルデッキのカードから小さいカードを2枚取り除くと、次のカードが10になる確率は32.00%になります。これは、ハード合計点でダブルを行う際に明らかに有利です。一方、8デッキのシューから小さいカードを2枚取り除くと、取り除く効果はそれほど強くなく、次のカードが10になる確率は30.92%に低下します。
各ルール変更のコストとベネフィットの最新表を以下に示します。ベネフィット合計0.689%が最終的なハウスエッジの差を上回っていることに注意してください。これは、スプリットの影響をまだ考慮していないためです。
ルールの効果
| ルール | シングルデッキ特典 |
|---|---|
| ディーラーの位置的優位性 | -0.079% |
| ブラックジャックで勝ったプレイヤーは3対2で配当される | 0.061% |
| プレイヤーはハード12から16でスタンドできる | 0.433% |
| プレイヤーはダブルできる | 0.273% |
| 合計 | 0.689% |
プレイヤーは分割可能
次に、スプリットが認められることによるプレイヤーの利益を分析しました。効果を検証するために、シミュレーションでは、デッキ数に応じた適切なスプリット戦略を実行しました。この戦略については、この記事の後半で説明します。この戦略を追加することで、完全な基本戦略が完成します。スプリットを追加した後は、プレイヤーとディーラーの間に検討すべきルールの違いは他にありません。完全な基本戦略におけるプレイヤーの期待収益は以下のとおりです。
- 1デッキ = -0.012%
- 8デッキ = -0.575%
このルールを追加するための行を含むシミュレーション結果テーブルは次のとおりです。
ルール変更による期待値
| ルール | 1つのデッキ | 8つのデッキ | 違い |
|---|---|---|---|
| ディーラーの位置的優位性 | -8.237% | -8.157% | -0.079% |
| ブラックジャックで勝ったプレイヤーは3対2で配当される | -5.912% | -5.894% | -0.018% |
| プレイヤーはハード12から16でスタンドできる | -2.209% | -2.625% | 0.415% |
| プレイヤーはダブルできる | -0.556% | -1.245% | 0.689% |
| プレイヤーは分割できる | -0.012% | -0.575% | 0.563% |
4 行目と 5 行目の違いは、プレイヤーが自由に分割できるという効果を示しています。
- 1デッキ = 0.544%
- 8デッキ = 0.669%
- 差 = -0.125%
これら 2 つの数字の差をとると、このルール変更の影響は、8 つのデッキのゲームと比較して、1 つのデッキのゲームのプレイヤーにとって 0.125% 少なくなることがわかります。
8デッキのゲームでは、1デッキのゲームよりもスプリットが有利な理由は、最初の2枚のカードでペアが出る確率が高くなるためです。具体的には、Excelの用語で言えば、8デッキの場合、確率は13*combin(4*8,2)/combin(52*8,2) = 7.470%です。1デッキの場合、確率は13*combin(4*1,2)/combin(52*1,2) = 5.882%です。
基本ゲームのルールでは、最大3回または4ハンドまで再スプリットが認められていることも覚えておいてください。1つのデッキから同じランクのカードが2枚取り除かれた場合、次のカードで同じランクのカードが出る確率は2/50 = 4.000%です。一方、8デッキのシューの場合、この確率は30/414 = 7.246%です。シングルデッキのゲームではスプリットと再スプリットの回数が少なくなるため、スプリットの価値は全体的に低くなります。これが、8デッキから1デッキにスプリットするメリットが減少する理由です。
シングルデッキ ゲームに分割のマイナス効果を加えると、8 つのデッキと比較したシングルデッキ ゲームの利点に対するさまざまなルールの影響を示す表が完成します。
ルール シングルデッキ メリット ディーラーのポジションアドバンテージ -0.079% 勝ったプレイヤーのブラックジャック配当は3対2 0.061% ハード12~16でスタンド可能 0.433% ダブル可能 0.273% スプリット可能 -0.125% 合計 0.563%右下のセルの合計値0.563%は、記事の冒頭で引用したハウスエッジ計算ツールで得られた差と一致していることに注目してください。同じ表を影響順に並べたものが以下です。
ルールの効果
| ルール | シングルデッキ特典 |
|---|---|
| ディーラーの位置的優位性 | -0.079% |
| ブラックジャックで勝ったプレイヤーは3対2で配当される | 0.061% |
| プレイヤーはハード12から16でスタンドできる | 0.433% |
| プレイヤーはダブルできる | 0.273% |
| プレイヤーは分割できる | -0.125% |
| 合計 | 0.563% |
基本戦略表
次の表は、与えられたルールと 1 つのデッキに適した基本戦略を示しています。
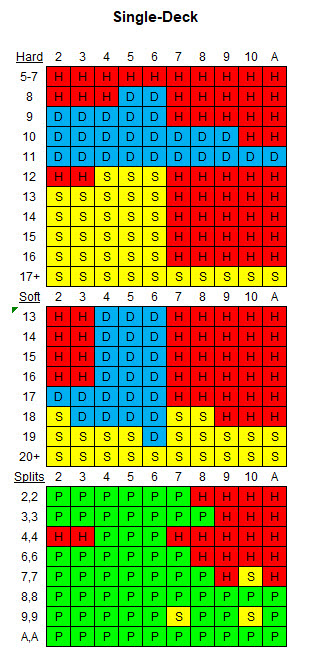
次の表は、与えられたルールと 8 つのデッキに適した基本戦略を示しています。
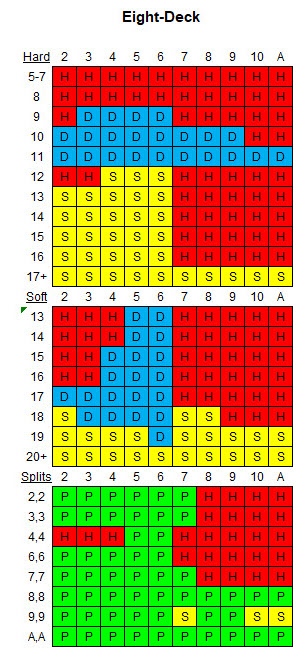
期待値表
以下の表は、シングルデッキゲームにおける各初期ハンドの期待値を示しています。一番上の行はディーラーのアップカードを示しています。期待値はディーラーがブラックジャックを確認する前に測定されています。合計列は、各行の期待値を、そのハンドを受け取る確率に基づいて加重平均したものです。右下のセルは、ゲーム全体の期待値を示しています。
シングルデッキゲームの期待値
1デッキでのプレイヤーの手札とディーラーのアップカードによる期待値
| プレーヤー | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | エース | 合計 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1278 | -0.0968 | -0.0379 | 0.0227 | 0.0403 | -0.1191 | -0.1805 | -0.2624 | -0.3654 | -0.5443 | -0.2169 |
| 6 | -0.1477 | -0.1037 | -0.0519 | 0.0104 | 0.0371 | -0.1640 | -0.2343 | -0.3046 | -0.4015 | -0.5713 | -0.2469 |
| 7 | -0.1120 | -0.0701 | -0.0119 | 0.0528 | 0.0683 | -0.0690 | -0.2232 | -0.2948 | -0.3863 | -0.5765 | -0.2211 |
| 8 | -0.0174 | 0.0199 | 0.0826 | 0.1407 | 0.1498 | 0.0921 | -0.0565 | -0.2135 | -0.3136 | -0.5144 | -0.1286 |
| 9 | 0.1124 | 0.1923 | 0.2837 | 0.3753 | 0.3799 | 0.1951 | 0.1111 | -0.0519 | -0.2165 | -0.4146 | 0.0151 |
| 10 | 0.4262 | 0.4908 | 0.5494 | 0.6276 | 0.6241 | 0.4458 | 0.3145 | 0.1644 | -0.0528 | -0.2991 | 0.2316 |
| 11 | 0.5428 | 0.5922 | 0.6516 | 0.7176 | 0.7198 | 0.4785 | 0.3417 | 0.2240 | 0.0670 | -0.1848 | 0.3268 |
| 12 | -0.2518 | -0.2255 | -0.1915 | -0.1364 | -0.1194 | -0.2273 | -0.2925 | -0.3639 | -0.4175 | -0.5824 | -0.3131 |
| 13 | -0.2879 | -0.2411 | -0.1816 | -0.1344 | -0.1208 | -0.2861 | -0.3461 | -0.3764 | -0.4590 | -0.6106 | -0.3415 |
| 14 | -0.2900 | -0.2391 | -0.1835 | -0.1342 | -0.1209 | -0.3442 | -0.3612 | -0.4192 | -0.4957 | -0.6356 | -0.3644 |
| 15 | -0.2803 | -0.2379 | -0.1837 | -0.1388 | -0.1266 | -0.3590 | -0.4133 | -0.4703 | -0.5397 | -0.6677 | -0。3893 |
| 16 | -0.2863 | -0.2446 | -0.1872 | -0.1435 | -0.1450 | -0.3760 | -0.4254 | -0.4797 | -0.5482 | -0.6739 | -0.3978 |
| 17 | -0.1568 | -0.1216 | -0.0712 | -0.0445 | -0.0306 | -0.1217 | -0.3976 | -0.4154 | -0.4562 | -0.6560 | -0.2947 |
| 18 | 0.1072 | 0.1359 | 0.1538 | 0.1983 | 0.2031 | 0.3887 | 0.0956 | -0.1961 | -0.2242 | -0.4527 | -0.0185 |
| 19 | 0.3763 | 0.3774 | 0.3965 | 0.4449 | 0.4364 | 0.6101 | 0.5769 | 0.2642 | 0.0125 | -0.1586 | 0.2644 |
| A,2 | 0.0402 | 0.0711 | 0.1174 | 0.2130 | 0.2455 | 0.1074 | 0.0392 | -0.0141 | -0.1454 | -0.3991 | -0.0057 |
| A,3 | 0.0184 | 0.0447 | 0.1127 | 0.2042 | 0.2391 | 0.0605 | 0.0349 | -0.0602 | -0.1781 | -0.4205 | -0.0308 |
| A,4 | -0.0103 | 0.0237 | 0.0892 | 0.1753 | 0.2191 | 0.0339 | -0.0354 | -0.1136 | -0.2226 | -0.4533 | -0.0697 |
| A,5 | -0.0298 | -0.0019 | 0.0667 | 0.1490 | 0.2327 | -0.0239 | -0.0842 | -0.1666 | -0.2760 | -0.4900 | -0.1094 |
| A,6 | 0.0142 | 0.0743 | 0.1549 | 0.2805 | 0.2630 | 0.0597 | -0.0646 | -0.1348 | -0.2383 | -0.4810 | -0.0586 |
| A,7 | 0.1279 | 0.1867 | 0.3091 | 0.3482 | 0.3623 | 0.4118 | 0.1209 | -0.0873 | -0.1926 | -0.4433 | 0.0459 |
| A,8 | 0.3953 | 0.4157 | 0.4100 | 0.4593 | 0.4666 | 0.6146 | 0.6078 | 0.2882 | -0.0009 | -0.1938 | 0.2686 |
| A,9 | 0.6525 | 0.6415 | 0.6507 | 0.6810 | 0.6730 | 0.7732 | 0.7848 | 0.7656 | 0.4594 | 0.0943 | 0.5871 |
| A,10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.4081 | 1.0409 | 1.4449 |
| あ、あ | 0.6384 | 0.6863 | 0.7417 | 0.8075 | 0.8289 | 0.6277 | 0.4865 | 0.3605 | 0.2080 | -0.1580 | 0.4744 |
| 2,2 | -0.0349 | 0.0396 | 0.1235 | 0.3014 | 0.3378 | 0.0137 | -0.1412 | -0.2224 | -0.3355 | -0.5246 | -0.1145 |
| 3,3 | -0.1082 | -0.0209 | 0.1607 | 0.3049 | 0.3395 | -0.0448 | -0.2232 | -0.3100 | -0.3986 | -0.5715 | -0.1646 |
| 4,4 | -0.0136 | 0.0268 | 0.1354 | 0.2680 | 0.2980 | 0.1104 | -0.0549 | -0.2063 | -0.3069 | -0.5065 | -0.0991 |
| 5.5 | 0.4441 | 0.5075 | 0.5870 | 0.6933 | 0.7084 | 0.4663 | 0.3227 | 0。1738 | -0.0510 | -0.2978 | 0.2444 |
| 6,6 | -0.0963 | 0.0132 | 0.1456 | 0.2786 | 0.1992 | -0.1933 | -0.3222 | -0.3862 | -0.4366 | -0.5989 | -0.2245 |
| 7,7 | -0.0546 | 0.0494 | 0.1879 | 0.2244 | 0.2396 | -0.0524 | -0.3804 | -0.4744 | -0.5556 | -0.6790 | -0.2508 |
| 8,8 | 0.1165 | 0.1873 | 0.2245 | 0.3287 | 0.3508 | 0.3040 | -0.0599 | -0.4017 | -0.4929 | -0.6389 | -0.1224 |
| 9,9 | 0.2052 | 0.2156 | 0.3070 | 0.4064 | 0.4080 | 0.4011 | 0.2067 | -0.0986 | -0.2041 | -0.4520 | 0.0666 |
| 10,10 | 0.6220 | 0.6323 | 0.6402 | 0.6718 | 0.6683 | 0.7647 | 0.7832 | 0.7440 | 0.4539 | 0.1383 | 0.5803 |
| 合計 | 0.1021 | 0.1388 | 0.1860 | 0.2391 | 0.2471 | 0.1473 | 0.0551 | -0.0435 | -0.1712 | -0.3891 | -0.0001 |
8デッキゲームの期待値
8デッキのプレイヤーの手札とディーラーのアップカードの期待値
| プレーヤー | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | エース | 合計 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.1258 | -0.0929 | -0.0562 | -0.0175 | 0.018 | -0.1196 | -0.1871 | -0.266 | -0.3663 | -0.5291 | -0.2191 |
| 6 | -0.1389 | -0.1042 | -0.0677 | -0.0287 | 0.0085 | -0.1534 | -0.2192 | -0.2941 | -0.3902 | -0.5469 | -0.2395 |
| 7 | -0.1094 | -0.0760 | -0.0391 | -0.0004 | 0.0349 | -0.0689 | -0.2121 | -0.2866 | -0.3731 | -0.5526 | -0.2164 |
| 8 | -0.0234 | 0.0076 | 0.0427 | 0.0774 | 0.1079 | 0.0831 | -0.0595 | -0.2104 | -0.3079 | -0.4931 | -0.1316 |
| 9 | 0.0743 | 0.1277 | 0.1921 | 0.2580 | 0.3141 | 0.1745 | 0.0998 | -0.0522 | -0.2180 | -0.3962 | -0.0071 |
| 10 | 0.3653 | 0.4176 | 0.4704 | 0.5253 | 0.5723 | 0.3990 | 0.2895 | 0.1469 | -0.0535 | -0.2865 | 0.2056 |
| 11 | 0.4786 | 0.5264 | 0.5759 | 0.6271 | 0.6718 | 0.4653 | 0.3496 | 0.2271 | 0.0864 | -0.2297 | 0.3097 |
| 12 | -0.2535 | -0.2331 | -0.2041 | -0.1613 | -0.1208 | -0.2146 | -0.2741 | -0.3430 | -0.4273 | -0.5746 | -0.3146 |
| 13 | -0.2867 | -0.2461 | -0.2030 | -0.1611 | -0.1210 | -0.2713 | -0.3264 | -0.3858 | -0.4682 | -0.6049 | -0.3447 |
| 14 | -0.2870 | -0.2456 | -0.2034 | -0.1612 | -0.1211 | -0.3240 | -0.3707 | -0.4295 | -0.5059 | -0.6328 | -0.3694 |
| 15 | -0.2858 | -0.2456 | -0.2033 | -0.1616 | -0.1217 | -0.3683 | -0.4162 | -0.4715 | -0.5422 | -0.6597 | -0.3927 |
| 16 | -0.2866 | -0.2463 | -0.2038 | -0.1622 | -0.1236 | -0.4103 | -0.4547 | -0.5057 | -0.5721 | -0.6820 | -0.4128 |
| 17 | -0.1565 | -0.1205 | -0.0819 | -0.0461 | -0.0090 | -0.1085 | -0.3842 | -0.4223 | -0.4633 | -0.6636 | -0.2958 |
| 18 | 0.1098 | 0.1379 | 0.1648 | 0.1953 | 0.2211 | 0.3982 | 0.1045 | -0.1847 | -0.2394 | -0.4626 | -0.0208 |
| 19 | 0.3780 | 0.3949 | 0.4138 | 0。4372 | 0.4513 | 0.6153 | 0.5918 | 0.2848 | -0.0149 | -0.1753 | 0.2569 |
| A,2 | 0.0458 | 0.0737 | 0.1041 | 0.1376 | 0.2024 | 0.1207 | 0.0523 | -0.0350 | -0.1703 | -0.3789 | -0.0269 |
| A,3 | 0.0224 | 0.0507 | 0.0827 | 0.1366 | 0.2010 | 0.0769 | 0.0155 | -0.0733 | -0.2024 | -0.4031 | -0.0533 |
| A,4 | -0.0006 | 0.0294 | 0.0641 | 0.1328 | 0.1986 | 0.0368 | -0.0282 | -0.1123 | -0.2357 | -0.4281 | -0.0803 |
| A,5 | -0.0211 | 0.0088 | 0.0611 | 0.1301 | 0.2004 | -0.0070 | -0.0689 | -0.1507 | -0.2691 | -0.4532 | -0.1057 |
| A,6 | -0.0006 | 0.0558 | 0.1220 | 0.1933 | 0.2513 | 0.0545 | -0.0721 | -0.1479 | -0.2563 | -0.4626 | -0.0792 |
| A,7 | 0.1160 | 0.1749 | 0.2418 | 0.3000 | 0.3560 | 0.4014 | 0.1074 | -0.0990 | -0.2075 | -0.4205 | 0.0270 |
| A,8 | 0.3800 | 0.3993 | 0.4157 | 0.4389 | 0.4621 | 0.6159 | 0.5953 | 0.2878 | -0.0164 | -0.1795 | 0.2579 |
| A,9 | 0.6371 | 0.6455 | 0.6562 | 0.6699 | 0.6778 | 0.7732 | 0.7909 | 0.7591 | 0.4379 | 0.1070 | 0.5752 |
| A,10 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.5000 | 1.3874 | 1.0388 | 1.4309 |
| あ、あ | 0.6072 | 0.6561 | 0.7062 | 0.7588 | 0.8058 | 0.6277 | 0.5001 | 0.3629 | 0.2059 | -0.1511 | 0.4411 |
| 2,2 | -0.0797 | -0.0089 | 0.0697 | 0.1700 | 0.2643 | 0.0087 | -0.1576 | -0.2385 | -0.3430 | -0.5115 | -0.1430 |
| 3,3 | -0.1305 | -0.0482 | 0.0500 | 0.1502 | 0.2425 | -0.0518 | -0.2189 | -0.2946 | -0.3899 | -0.5465 | -0.1859 |
| 4,4 | -0.0225 | 0.0080 | 0.0441 | 0.1066 | 0.2027 | 0.0857 | -0.0595 | -0.2096 | -0.3070 | -0.4921 | -0.1212 |
| 5.5 | 0.3676 | 0.4201 | 0.4748 | 0.5324 | 0.5814 | 0.4012 | 0.2910 | 0.1477 | -0.0534 | -0.2863 | 0.2074 |
| 6,6 | -0.1947 | -0.0972 | 0.0043 | 0.1075 | 0.1900 | -0.2189 | -0.2775 | -0.3453 | -0.4295 | -0.5767 | -0.2426 |
| 7,7 | -0.1233 | -0.0335 | 0.0669 | 0.1569 | 0.2508 | -0.0485 | -0.3765 | -0.4361 | -0.5129 | -0.6382 | -0.2497 |
| 8,8 | 0.0720 | 0.1452 | 0.2171 | 0.3005 | 0.3753 | 0.3195 | -0.0276 | -0.3893 | -0.5170 | -0.6660 | -0.1329 |
| 9,9 | 0。1943 | 0.2506 | 0.3196 | 0.3925 | 0.4551 | 0.3996 | 0.2308 | -0.0801 | -0.2369 | -0.4624 | 0.0585 |
| 10,10 | 0.6334 | 0.6442 | 0.6549 | 0.6688 | 0.6770 | 0.7723 | 0.7907 | 0.7566 | 0.4373 | 0.1124 | 0.5745 |
| 合計 | 0.0927 | 0.1262 | 0.1628 | 0.2025 | 0.2390 | 0.1453 | 0.0585 | -0.0403 | -0.1727 | -0.3712 | -0.0058 |
期待値の差(%)
次の表は、シングルデッキ ゲームの期待値から 8 デッキ ゲームの期待値をパーセントで示しています。
プレイヤーの手札とディーラーのアップカードによる期待値の変化(×100)
| プレーヤー | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | エース | 合計 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0.196 | -0.383 | 1.834 | 4.02 | 2.229 | 0.05 | 0.664 | 0.361 | 0.087 | -1.52 | 0.22 |
| 6 | -0.8770 | 0.0480 | 1.5840 | 3.9030 | 2.8630 | -1.0640 | -1.5170 | -1.0490 | -1.1320 | -2.4330 | -0.7380 |
| 7 | -0.2560 | 0.5920 | 2.7210 | 5.3240 | 3.3400 | -0.0070 | -1.1090 | -0.8160 | -1.3150 | -2.3840 | -0.4720 |
| 8 | 0.6060 | 1.2300 | 3.9870 | 6.3300 | 4.1900 | 0.9040 | 0.3020 | -0.3070 | -0.5740 | -2.1370 | 0.2910 |
| 9 | 3.8080 | 6.4600 | 9.1610 | 11.7320 | 6.5770 | 2.0670 | 1.1320 | 0.0300 | 0.1480 | -1.8380 | 2.2220 |
| 10 | 6.0970 | 7.3170 | 7.8980 | 10.2270 | 5.1830 | 4.6820 | 2.4980 | 1.7530 | 0.0720 | -1.2510 | 2.6040 |
| 11 | 6.4200 | 6.5830 | 7.5650 | 9.0560 | 4.8030 | 1.3220 | -0.7900 | -0.3170 | -1.9460 | 4.4940 | 1.7050 |
| 12 | 0.1670 | 0.7540 | 1.2640 | 2.4890 | 0.1350 | -1.2760 | -1.8390 | -2.0880 | 0.9840 | -0.7830 | 0.1460 |
| 13 | -0.1260 | 0.5070 | 2.1460 | 2.6670 | 0.0210 | -1.4780 | -1.9700 | 0.9410 | 0.9190 | -0.5660 | 0.3180 |
| 14 | -0.2970 | 0.6510 | 1.9930 | 2.6980 | 0.0150 | -2.0210 | 0.9460 | 1.0330 | 1.0240 | -0.2860 | 0.5000 |
| 15 | 0.5560 | 0.7690 | 1.9570 | 2.2820 | -0.4950 | 0.9270 | 0.2900 | 0.1190 | 0.2470 | -0.7990 | 0.3400 |
| 16 | 0.0300 | 0.1700 | 1.6680 | 1.8640 | -2.1330 | 3.4380 | 2.9220 | 2.6000 | 2.3870 | 0.8060 | 1.4950 |
| 17 | -0.0300 | -0.1100 | 1.0720 | 0.1630 | -2.1630 | -1.3190 | -1.3380 | 0.6910 | 0.7130 | 0.7580 | 0.1060 |
| 18 | -0.2560 | -0.2000 | -1.0990 | 0.2950 | -1.7950 | -0.9490 | -0.8890 | -1.1420 | 1.5210 | 0.9900 | 0.2340 |
| 19 | -0。1730 | -1.7470 | -1.7360 | 0.7660 | -1.4910 | -0.5200 | -1.4980 | -2.0590 | 2.7370 | 1.6770 | 0.7460 |
| A,2 | -0.5660 | -0.2590 | 1.3280 | 7.5340 | 4.3080 | -1.3290 | -1.3120 | 2.0900 | 2.4910 | -2.0210 | 2.1220 |
| A,3 | -0.4090 | -0.6000 | 3.0040 | 6.7580 | 3.8040 | -1.6410 | 1.9440 | 1.3040 | 2.4300 | -1.7440 | 2.2470 |
| A,4 | -0.9750 | -0.5720 | 2.5100 | 4.2580 | 2.0490 | -0.2980 | -0.7230 | -0.1290 | 1.3080 | -2.5210 | 1.0610 |
| A,5 | -0.8730 | -1.0720 | 0.5650 | 1.8950 | 3.2330 | -1.6930 | -1.5280 | -1.5890 | -0.6930 | -3.6740 | -0.3690 |
| A,6 | 1.4820 | 1.8480 | 3.2870 | 8.7240 | 1.1650 | 0.5180 | 0.7480 | 1.3090 | 1.7920 | -1.8340 | 2.0600 |
| A,7 | 1.1920 | 1.1830 | 6.7250 | 4.8180 | 0.6310 | 1.0410 | 1.3420 | 1.1640 | 1.4890 | -2.2860 | 1.8940 |
| A,8 | 1.5370 | 1.6390 | -0.5690 | 2.0370 | 0.4540 | -0.1320 | 1.2540 | 0.0390 | 1.5550 | -1.4310 | 1.0640 |
| A,9 | 1.5370 | -0.3990 | -0.5560 | 1.1160 | -0.4780 | 0.0020 | -0.6060 | 0.6480 | 2.1530 | -1.2700 | 1.1970 |
| A,10 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.0730 | 0.2070 | 1.3970 |
| あ、あ | 3.1200 | 3.0230 | 3.5450 | 4.8720 | 2.3070 | 0.0000 | -1.3620 | -0.2430 | 0.2140 | -0.6920 | 3.3340 |
| 2,2 | 4.4790 | 4.8510 | 5.3790 | 13.1380 | 7.3480 | 0.4980 | 1.6370 | 1.6100 | 0.7540 | -1.3140 | 2.8470 |
| 3,3 | 2.2320 | 2.7290 | 11.0750 | 15.4710 | 9.7010 | 0.7020 | -0.4300 | -1.5380 | -0.8700 | -2.4920 | 2.1250 |
| 4,4 | 0.8840 | 1.8800 | 9.1320 | 16.1400 | 9.5290 | 2.4760 | 0.4550 | 0.3380 | 0.0090 | -1.4460 | 2.2100 |
| 5.5 | 7.6550 | 8.7410 | 11.2230 | 16.0940 | 12.6990 | 6.5150 | 3.1720 | 2.6130 | 0.2380 | -1.1510 | 3.7020 |
| 6,6 | 9.8410 | 11.0360 | 14.1250 | 17.1060 | 0.9170 | 2.5610 | -4.4720 | -4.0910 | -0.7110 | -2.2180 | 1.8060 |
| 7,7 | 6.8730 | 8.2850 | 12.1030 | 6.7540 | -1.1240 | -0.3840 | -0.3830 | -3.8370 | -4.2660 | -4.0800 | -0.1170 |
| 8,8 | 4.4530 | 4.2080 | 0.7370 | 2.8160 | -2.4470 | -1.5490 | -3.2240 | -1.2460 | 2.4110 | 2.7050 | 1.0500 |
| 9,9 | 1.0910 | -3.5070 | -1.2560 | 1.3820 | -4.7120 | 0.1480 | -2.4060 | -1.8530 | 3.2860 | 1.0450 | 0.8060 |
| 10,10 | -1.1490 | -1.1970 | -1.4750 | 0.2960 | -0.8740 | -0.7630 | -0.7510 | -1.2620 | 1.6580 | 2.5910 | 0.5780 |
| 合計 | 0.9370 | 1.2510 | 2.3110 | 3.6590 | 0.8050 | 0.1970 | -0.3390 | -0.3210 | 0.1480 | -1.7900 | 0.5620 |
さらに読む
ピーター・グリフィン著『ブラックジャックの理論』は、この記事のテーマを私が知る限り最も的確に扱っています。彼は第8章「多くのデッキと異なるルール」でこのテーマを取り上げており、異なる基本ルールセットを用いて、1つのデッキと無限のデッキの違いを計算しています。彼は常に正確な数値を示しているわけではありませんが、自身の仮定に基づく0.69%の差の内訳を以下のように言い換えています。
- 倍増:0.69%のほぼ半分
- プレイヤーのブラックジャック: 0.07%
- スプリット:ブラックジャックの利益を相殺する以上のもの
- 12 から 16 について: 「おそらく残りの矛盾です。」
グリフィンは、1 つのデッキと無限のデッキの両方におけるさまざまなルール変更の利点を列挙しています。
謝辞
この記事の分析と校正に関して賢明な助言をくださったドン・シュレシンジャー氏に感謝申し上げます。


