このページ
各ベットのハウスエッジの算出方法
概要
導入
クラップスの付録へようこそ。ここでは、クラップスにおける主要なベット全てにおけるプレイヤーエッジを導き出します。この付録以外では、通常ハウスエッジについて言及します。これはプレイヤーエッジに-1を掛けたものです。すべてのベットに-1を掛けるのを避けるため、ここでは全てをプレイヤーエッジで説明します。フリーオッズを除く全てのベットにおいて、ハウスエッジは最終的にマイナスになるため、プレイヤーエッジはマイナスになることが予想されます。しばらくお時間を取って、いくつかのベットを実際に試してみて下さい。オッズへの理解が深まるだけでなく、数学スキルを復習したり、向上させたりするきっかけになれば幸いです。
先に進む前に、各合計が1回で出る確率を理解しておく必要があります。これは、私のサイコロの確率の基礎ページで詳しく説明しています。6が出る確率が5/36であることを知らなかったり、理解できなかったりする場合は、このページを読む前に、そのページをご覧ください。
賭けの期待収益の一般的な公式は次のとおりです。
すべての可能な結果にわたる∑ (イベント i の確率) × (イベント i の収益)。
プレイヤーのエッジは、期待収益を初期ベット額で割ったものです。例えば、スポーツイベントでラインに逆らって賭ける場合、10ドルを獲得するには11ドルを賭ける必要があります。勝率が50%だとすると、期待収益は0.5×(10) + 0.5×(-11) = -0.5となります。プレイヤーのエッジは-0.5/11 = -1/22 ≈ -4.545%となります。
ハウスエッジのルールの例外は、タイが発生する可能性がある場合です。一般的に、ハウスエッジの計算ではタイは無視されます。タイが発生する可能性がある場合、この影響を考慮するには、期待リターンを解決された平均ベット額で割ります。「解決された平均ベット額」とは、最初の賭け金とベットが解決された確率の積です。クラップスでは、タイが発生するベットはドントパスとドントカムのみです。
クラップスの賭けの多くは、ある特定のイベントが別のイベントよりも先に起こった場合に勝ちます。これらの賭けは、結果が出るまでに複数回のロール、あるいはそれ以上の回数を要することがあります。賭けが確率pで勝ち、確率qで負け、確率1-pqで有効のままだとすると、最終的に勝つ確率は次のようになります。
∑ p×(1-pq) i (i=0から無限大) =
p × (1/(1-(1-pq))) = p × (1/(p+q)) = p/(p+q)。
このページでは、p/(p+q) という形式の式を多数目にします。スペースを節約するため、式は既に上で導出済みなので、毎回導出することはしません。
パス/カム
カムアウトロールで勝つ確率はpr(7)+pr(11) = 6/36 + 2/36 = 8/36です。
ポイントを獲得して勝利する確率は、pr(4)×pr(4 before 7) + pr(5)×pr(5 before 7) + pr(6)×pr(6 before 7) + pr(8)×pr(8 before 7) + pr(9)×pr(9 before 7) + pr(10)×pr(10 before 7) =
(3/36)×(3/9) + (4/36)×(4/10) + (5/36)×(5/11) + (5/36)×(5/11) + (4/36)×(4/10) + (3/36)×(3/9) =
(2/36) × (9/9 + 16/10 + 25/11) =
(2/36) × (990/990 + 1584/990 + 2250/990) =
(2/36) × (4824/990) = 9648/35640
全体の当選確率は8/36 + 9648/35640 = 17568/35640 = 244/495
負ける確率は明らかに1-(244/495) = 251/495である。
したがって、プレイヤーの優位性は (244/495)×(+1) + (251/495)×(-1) = -7/495 ≈ -1.414% となります。
通らない/来ない
カムアウトロールで勝つ確率はpr(2)+pr(3) = 1/36 + 2/36 = 3/36です。
カムアウトロールでプッシュする確率はpr(12) = 1/36です。
ポイントを獲得して勝利する確率は、pr(4)×pr(7 before 4) + pr(5)×pr(7 before 5) + pr(6)×pr(7 before 6) + pr(8)×pr(7 before 8) + pr(9)×pr(7 before 9) + pr(10)×pr(7 before 10) =
(3/36)×(6/9) + (4/36)×(6/10) + (5/36)×(6/11) + (5/36)×(6/11) + (4/36)×(6/10) + (3/36)×(6/9) =
(2/36) × (18/9 + 24/10 + 30/11) =
(2/36) × (1980/990 + 2376/990 + 2700/990) =
(2/36) × (7056/990) = 14112/35640
勝利の確率は3/36 + 14112/35640 = 17082/35640 = 2847/5940です。
負ける確率は1-(2847/5940 + 1/36) = 1-(3012/5940) = 2928/5940
期待収益率は2847/5940×(+1) + 2928/5940×(-1) = -81/5940 = -3/220 ≈ 1.364%
クラップスに関する他の多くの情報源では、ドントパスベットのハウスエッジは1.403%であると主張しています。この食い違いの原因は、タイをカウントするかどうかにあります。私はタイをマネーベットとしてカウントすることを好みますが、そうでない人もいます。どちらが正しいとか間違っているとか言っているのではなく、私はタイをカウントすることを好んでいるというだけです。引き分けを賭け金としてカウントしない場合は、上記の数字を、賭けが勝ちまたは負けになる確率(35/36)で割る必要があります。つまり、1.364%/(35/36) ≈ -1.403%となります。これは、プレイヤーがカムアウトロールで12を出さないと仮定した場合のハウスエッジです。
勝つために賭ける
6か8に賭ける: [(5/11)×7 + (6/11)×(-6)]/6 = (-1/11)/6 = -1/66 ≈ -1.515%
5か9に賭ける: [(4/10)×7 + (6/10)×(-5)]/5 = (-2/10)/5 = -1/25 = -4.000%
4または10に賭ける:[(3/9)×9 + (6/9)×(-5)]/5 = (-3/9)/5 = -1/15 ≈ -6.667%
負けるために賭ける
6か8で負ける賭け:[(6/11)×4 + (5/11)×(-5)]/5 = (-1/11)/5 = -1/55 ≈ -1.818%
5か9で負ける賭け:[(6/10)×5 + (4/10)×(-8)]/8 = (-2/10)/8 = -1/40 = -2.500%
4または10で負ける賭け:[(6/9)×5 + (3/9)×(-11)]/11 = (-3/9)/11 = -1/33 ≈ -3.030%
注:これらの賭けは実際のカジノでは許可されていません。一部のインターネットカジノでのみ利用可能です。
買う
6または8に賭ける場合:[(5/11)×23 + (6/11)×(-21)]/21 = (-11/11)/21 = -1/21 ≈ -4.762%
5または9に賭ける場合:[(4/10)×29 + (6/10)×(-21)]/21 = (-10/10)/21 = -1/21 = -4.762%
4または10に賭ける場合:[(3/9)×39 + (6/9)×(-21)]/21 = (-9/9)/21 = -1/21 ≈ -4.762%
横たわる
6または8で負けるレイベット:[(6/11)×19 + (5/11)×(-25)]/25 = (-11/11)/25 = -1/25 ≈ -4.000%
5または9で負けるレイベット:[(6/10)×19 + (4/10)×(-31)]/31 = (-10/10)/31 = -1/31 = -3.226%
4または10で負けるレイベット:[(6/9)×19 + (3/9)×(-41)]/41 = (-9/9)/41 = -1/41 ≈ -2.439%
ビッグ6/ビッグ8
[(5/11)×1 + (6/11)×(-1)]/1 = -1/11 ≈ 9.091%
ハード4/ハード10
注:ハード 4 とハード 10 は 7対1、つまり 8対1 で支払われます。クラップスでは、上記のグラフを含め、布のオッズは 1 対 1 ベースでリストされています。
任意のロールでハード 4 が出る確率は 1/36 です。
任意のロールで 7 が出る確率は 6/36 です。
任意のロールでソフト 4 が出る確率は 2/36 (1+3 と 3+1) です。
どのロールでも勝つ確率は 1/36 です。
任意のロールで負ける確率は、6/36 + 2/36 = 8/36 です。
賭けに勝つ確率はp/(p+q)(上記参照)=(1/36)/(9/36)=1/9である。
期待収益は(1/9)×7 + (8/9)×(-1) = -1/9 ≈ 11.111%です。
賭け金が 1 ユニットなので、プレイヤーのエッジも -1/9 になります。
ハード 10 でも確率は同じです。
ハード6/ハード8
注:ハード 4 とハード 10 は 9対1、つまり 10対1 で支払われます。クラップスでは、上記のグラフを含め、布のオッズは 1 対 1 ベースでリストされています。
任意のロールでハード 6 が出る確率は 1/36 です。
任意のロールで 7 が出る確率は 6/36 です。
任意のロールでソフト 6 が出る確率は 4/36 (1+5、2+3、3+2、および 5+1) です。
どのロールでも勝つ確率は 1/36 です。
任意のロールで負ける確率は、6/36 + 4/36 = 10/36 です。
賭けに勝つ確率はp/(p+q)(上記参照)=(1/36)/(11/36)=1/11である。
期待収益は(1/11)×9 + (10/11)×(-1) = -1/11 ≈ 9.091%です。
賭け金が 1 ユニットなので、プレイヤーのエッジも -1/11 になります。
ハード 8 でも確率は同じです。
クラップス 2/クラップス 12
[(1/36)×30 + (35/36)×(-1)]/1 = -5/36 ≈ -13.889%
クラップス 3/クラップス 11
[(2/36)×15 + (34/36)×(-1)]/1 = -4/36 ≈ -11.111%
クラップス
[(4/36)×7 + (32/36)×(-1)]/1 = -4/36 ≈ -11.111%
どれでも7
[(6/36)×4 + (30/36)×(-1)]/1 = -6/36 ≈ -16.667%
ホーン
2 または 12 が出る確率は 1/36 + 1/36 = 2/36 です。
3 または 11 が出る確率は 2/36 + 2/36 = 4/36 です。
それ以外の目が出る確率は、1-2/36-4/36 = 30/36 です。
ホーンベットはクラップスの4つのベットを1つにまとめたものなので覚えておいてください。1つ勝ったとしても、他の3つは負けます。ハウスエッジは以下のとおりです。
[(2/36)×27 + (4/36)×12 + (30/36)×(-4)]/4 = (-18/36)/4 = 12.500%
分野
12 が 2:1 で支払われる場合、期待される収益は次のようになります。
2×(pr(2)+pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
2×(1/36 + 1/36) + 1×(2/36 + 3/36+ 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36+ 4/36) =
2×(2/36) + 1×(14/36) + -1×(20/36) = -2/36 = -1/18 ≈ 5.556%。
12 が 3:1 で支払われる場合、期待される収益は次のようになります。
3×pr(2) + 2×pr(12)) + 1×(pr(3)+pr(4)+pr(5)+pr(10)+pr(11)) + -1×(pr(6)+pr(7)+pr(8)+pr(9)) =
3×(1/36) + 2×(1/36) + 1×(2/36 + 3/36+ 4/36 + 3/36 + 2/36) + -1×(5/36 + 6/36 + 5/36+ 4/36) =
3×(1/36) + 2×(1/36) + 1×(14/36) + -1×(20/36) = -1/36 ≈ 2.778%。
購入オッズ
4と10: [(3/9)×2 + (6/9)×(-1)]/1 = 0.000%
5と9: [(4/10)×3 + (6/10)×(-2)]/2 = 0.000%
6と8: [(5/11)×6 + (6/11)×(-5)]/5 = 0.000%
オッズを賭ける
4と10: [(6/9)×1 + (3/9)×(-2)]/1 = 0.000%
5と9: [(6/10)×2 + (4/10)×(-3)]/2 = 0.000%
6と8: [(6/11)×5 + (5/11)×(-6)]/5 = 0.000%
パスと購入のオッズの組み合わせ
パスラインとバイイングオッズを組み合わせた場合のプレイヤーエッジは、平均的なプレイヤーのゲインを平均的なプレイヤーのベットで割ったものです。パスラインのゲインは常に-7/495、オッズのゲインは常に0です。期待されるベット額は、許容されるオッズの倍数によって異なります。フルダブルオッズ、つまりパスラインのベット額が2ドル、4、5、9、10のオッズが4ドル、6または8のオッズが5ドルだと仮定しましょう。
平均ゲインは -2×(7/495) = -14/495 です。
平均賭け金は2 + (3/36)×4 + (4/36)×4 + (5/36)×5 + (5/36)×5 + (4/36)×4 + (3/36)×4] =
2 + 106/36 = 178/36
プレイヤーの優位性は (-14/495)/(178/36) = -0.572% です。
6と8にx倍のオッズ、5と9にy倍のオッズ、4と10にz倍のオッズを取ることができる場合の一般的な公式は、(-7 / 495) / [ 1 + ((5x + 4y + 3z) / 18) ]です。
ドントパスとレイディングオッズの組み合わせ
ドントパスとレイドオッズを組み合わせた場合のプレイヤーエッジは、平均的なプレイヤーのゲインを平均的なプレイヤーのベットで割ったものです。ドントパスのゲインは常に-3/220、オッズのゲインは常に0です。期待されるベット額は、許容されるオッズの倍数によって異なります。例えば、ダブルオッズでドントパスに10ドルを賭けるとします。この場合、プレイヤーは4と10で20ドルの勝利を得るために40ドルのオッズを、5と9で20ドルの勝利を得るために30ドルのオッズを、6と8で20ドルの勝利を得るために24ドルのオッズを賭けることができます。平均的なゲインは-10×(3/220) = -30/220です。
平均賭け金は10 + 2×[(3/36)×40 + (4/36)×30 + (5/36)×24] = 30です。
プレイヤーの優位性は (-30/220)/30 = -0.455% です。
一般的な公式では、x 倍のオッズを購入できる場合、ドント パスとレイイング オッズを組み合わせたハウス エッジは (3/220)/(1+x) になります。
セッションあたりの純利益/損失
下のチャートは、100回の試行、つまりカムアウトロールで予想される純利益または純損失を示しています。このチャートを作成するにあたり、プレイヤーはパスラインに1ドルを賭け、ダブルオッズをフルベットします。
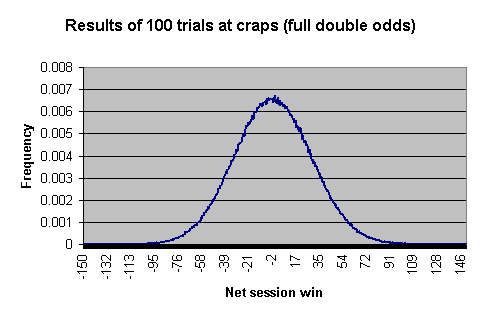
さまざまな間隔に該当する確率を示す実際の数値を以下に示します。
セッションの勝敗
| 間隔 | 確率 |
|---|---|
| 100ドル以上の損失 | 0.0422% |
| 76~100ドルの損失 | 0.6499% |
| 51ドルから75ドルの損失 | 4.6414% |
| 26~50ドルの損失 | 16.3560% |
| 1~25ドルの損失 | 30.0583% |
| とんとん | 0.6743% |
| 1ドルから25ドルの勝利 | 28.6368% |
| 26ドルから50ドルの勝利 | 14.4257% |
| 51ドルから75ドルの勝利 | 3.9097% |
| 76ドルから100ドルの勝利 | 0.5639% |
| 100ドル以上の勝利 | 0.0418% |
グラフと表は、100 回の試行またはカムアウト ロールを 1,000,000 回シミュレートし、各セッションの結果を表にして作成されました。
内部リンク
- 各ベットのハウスエッジがどのように算出されるかを簡単に説明します。
- 全ての主要な賭けのハウスエッジは、賭けごととロールごとの両方で計算されます。
- サイコロ制御実験。巧みなサイコロ投げに関する2つの実験の結果。
- ダイスコントロールの優位性。プレイヤーがダイスを操作できると仮定した場合の優位性。
- クラップスのバリエーション。ファイアーベット、クラップレスクラップス、カードクラップスなどの代替ルールと賭け方。
- カリフォルニア・クラップス。トランプを使ってカリフォルニアでクラップスをプレイする方法。
- クラップスをプレイしましょう。サンディエゴのビエハス カジノでカードを使ったクラップス ゲームをプレイしましょう。
- ロール回数表。シューターが7アウトになるまでに1~200ロール続ける確率。
- ウィザードに質問。私が回答したクラップスに関する質問をご覧ください。
- シンプルなクラップスゲーム。Javaで作ったシンプルなクラップスゲーム。


