スポーツ - よくある質問
バルガス対クォーティのボクシング試合の現在のオッズは、バルガスが-240、クォーティが+190です。バルガスに100ドル、またはクォーティに100ドル賭けた場合、どうなりますか?
バルガスに240ドルの賭けをすると100ドルが得られます。クァーティーに100ドルの賭けをすると190ドルが得られます。もちろん、任意の金額を賭けることができますが、利益は同じ比率になります。例えば、バルガスに100ドル賭けた場合、100 × (100/240) = 41.67ドルが得られます。
スプレッドに賭けるスポーツベッティングでは、負けた人ではなく勝った人が10%の手数料を支払うように思います。何か見落としている点はありますか?
どちらの見方もできます。例えば、あるゲームで11ドルを賭けて10ドルを獲得したとします。
負けた方が支払う:これはイーブンマネーベットとも言えますが、勝った場合は1ドルの手数料が返金されます。つまり、手数料を支払うのは負けた人だけです。
勝者への配当:公平なイーブンマネーベットであれば、11ドルの賭け金で11ドルの配当が得られます。しかし、賭けが勝った場合、勝者は10ドルしか得られません。この1ドルは手数料または料金とみなすことができます。
私個人としては、勝率が 50% だと仮定すると、どちらも 4.54% のハウス エッジの形で支払われると考えています。
ネバダ州以外に、野球やフットボールなどのプロスポーツに賭けることが合法な州はありますか?
ネバダ州以外でスポーツ賭博が合法化されているのはデラウェア州だけです。デラウェア州では宝くじで運営されているため、当選確率はかなり低いです。
最近、開催されていたフットボールプールを見ていました。これは、100個のマス目があり、X軸とY軸に沿って0から9までの数字が並び、スコアの最後の数字に対応するタイプのものでした。私はフットボールファンではないので、このプールには賭けませんでしたが、ギャンブラーなので、それほど魅力的な賭けではないと思っています。
私が言及しているプールの種類をご存知だと仮定しています。各ボックスの価格は5ドルで、配当は四半期ごとに支払われます。ボックスが当たれば125ドルの賞金がもらえますが、最後の数字が同じであれば4四半期すべて当選して500ドルを獲得し、配当は100対1になる可能性があります。
賭けを勧誘した人は、500ドルの当選確率は100対1だと言っていましたが、私は同意しません。まず、0と7のボックスは2と9のボックスよりも当選確率がはるかに高いです。しかし、ゲーム全体を通して最後の2つの数字が0と7のままになる確率は高いはずです。もしボックスがランダムに選ばれるとしたら、500ドルの賞金が当たる確率はどれくらいでしょうか?
グリッド内のセルがランダムに選択されると仮定すると、いずれかの四半期で勝利する確率は1/100になります。各四半期が独立したイベントであると仮定すると(実際にはそうではありませんが)、4つの四半期すべてで勝利する確率は(1/100) 4 = 1億分の1になります。
最新の「魔法使いに聞く」セクションを読みました。スポーツベッティングは生計を立てる手段の一つだとおっしゃっていましたね。もう少し詳しく説明していただけますか?ブラックジャックでカードカウンティングを駆使してカジノに勝つのと同じような優位性がブックメーカーにあるのか?ありがとうございます。
残念ながら、あまり詳しくお話しできません。スポーツベッティングは得意ではありませんが、時間があればもっと勉強するつもりです。スポーツベッティングの収益性をカードカウンティングと比較するのは難しいと言わざるを得ません。カードカウンティングは非常に技術的で、決まりきったことです。スポーツベッティングで儲けるには、より多くの判断力と、より個人的な意見が反映される必要があります。スポーツベッティングで儲けるには、様々な戦略があります。例えば、異なるカジノで異なるポイントスプレッドで両サイドに賭けるアービトラージゲーム、珍しいプロポジションベット、相関性のあるパーレーを狙うなどです。スポーツベッティングで勝つためのより詳しい情報については、スタンフォード・ウォン著『Sharp Sports Betting』をお勧めします。
NFLのハンディキャッパーが、自分の予想の勝率を自慢しているのを何度も見てきました。ランダムに選んだ人が、1シーズン、3シーズン、5シーズンで50%、55%、60%の勝率を出す確率はどれくらいでしょうか?
以下の表は、1シーズンから5シーズンまでの各シーズン数ごとに、50%から60%までの各パーセンテージを1%ずつ増加させて達成する確率を示しています。これは259試合のシーズンに基づいています。また、全体のパーセンテージは切り捨てられていると仮定しています。例えば、ハンディキャッパーが259試合中132試合を予想し、パーセンテージが50.97%だった場合、実際には51%には達していないため、50%を予想したとしか評価されません。これらの自慢げなハンディキャッパーが、自分に有利なように切り捨てているとしても不思議ではありません。
NFLにおけるハンディキャップ率の確率
| 比率 | 1シーズン | 2シーズン | 3シーズン | 4つの季節 | 5つの季節 |
| 0.5 | 0.5 | 0.517523 | 0.5 | 0.512393 | 0.5 |
| 0.51 | 0.354641 | 0.314437 | 0.282985 | 0.257059 | 0.234993 |
| 0.52 | 0.267178 | 0.178085 | 0.125486 | 0.101366 | 0.074229 |
| 0.53 | 0.160065 | 0.086589 | 0.049447 | 0.025155 | 0.015098 |
| 0.54 | 0.106982 | 0.035817 | 0.013066 | 0.004959 | 0.001926 |
| 0.55 | 0.053095 | 0.012519 | 0.002569 | 0.000687 | 0.000152 |
| 0.56 | 0.023385 | 0.00282 | 0.000373 | 0.000051 | 0.000007 |
| 0.57 | 0.012645 | 0.00067 | 0.000053 | 0.000003 | 0 |
| 0.58 | 0.00453 | 0.000133 | 0.000004 | 0 | 0 |
| 0.59 | 0.00213 | 0.000022 | 0 | 0 | 0 |
| 0.6 | 0.000617 | 0.000003 | 0 | 0 | 0 |
NFLプールについてご意見をお聞かせください。チケットは1枚25ドルで、ランダムに選ばれた3チームが所定の順番で選出されます。毎週、正しい順番で上位3チームを選んだチケット所有者に1,000ドルが贈られます。各チケットの実際の価値はいくらですか?
NFLシーズンは17週、32チームで構成されています。ある週の優勝確率は、32×31×30 = 29760分の1です。チケット1枚の期待値は、1000ドル×17/29760 = 57.12セントです。つまり、期待リターンは2.28%、ハウスエッジは97.72%となります。
ウェブページにも書いてあるように、ご迷惑をおかけして申し訳ありませんが、数学の才能を使ってスポーツ賭博のオッズの異常値を見つけたり、その情報に基づいて保証された利益を得る方法を計算したりしたことがありますか?
ここ数年、私は他のギャンブルよりもずっと多くの時間をスポーツベッティングに費やしてきました。異なるラインで2つのスポーツブックを対戦させない限り(これは非常に稀なケースですが)、スポーツベッティングで確実に儲ける方法はありません。秘密を明かすのは時期尚早ですが、私はプレイヤーに有利と思われる賭けを探し、賭けをするようにしています。最近私が作成したスポーツベッティングに関する付録2もぜひご覧ください。
ある大学のフットボール チームが第 1 試合に勝つ確率が 10%、第 2 試合に勝つ確率が 30%、両方の試合に負ける確率が 65% の場合、正確に 1 回勝つ確率はどれくらいでしょうか。
両試合が独立していると仮定した場合、両試合に負ける確率は90%×70%=63%となります。しかし、両試合に負ける確率は実際には65%(63%よりも高い)だとおっしゃっているので、両試合は相関関係にあることになります。両試合に負ける確率が65%で、第2試合に負ける確率が70%だとすると、第1試合に勝ち、第2試合に負ける確率は5%になります。同じ論理で、第1試合に負け、第2試合に勝つ確率は25%になります。つまり、両試合に勝つ確率は5%しか残らないということです。つまり、両試合に勝つ確率は25%+5%=30%となります。
今夜のマンデーナイトフットボール(ダラス対ワシントン)について質問させてください。ワシントンでは数時間前から雨が降っています。この雨は試合中だけでなく翌日も続くでしょう。雨はNFLのオーバー/アンダーベットにどのような影響を与えますか?何か傾向やアドバイスはありますか?
雨がトータルにどのような影響を与えるかは分かりません。しかし、鋭いハンディキャッパーは天候を非常に重視し、気温、降水量、風速などを考慮してラインを移動させることは知っています。
こんにちは、ウィズ。例えば、1,000ドルの賭けで年間80,000ドルの利益を得られるスポーツベッティングシステムを思いついたとします。この利益を出すには、年間約250~300回の賭けが必要です。カジノがカードカウンターを締め出すのと同じように、スポーツブックも私を締め出すのでしょうか?公然とスポーツベッターとして成功できるのでしょうか?それとも、カードカウンターのようにこっそりと活動する必要があるのでしょうか?
まず、1,000ドルの賭け金で、資金がわずか250~300ドルで8万ドルも稼げる人がいるとは思えません。それに、「システム」という言葉については、もう触れないでおきます。あなたの質問に答えると、最高のスポーツベッターは大抵、公然と賭けをしています。たとえスポーツブックがプロの賭けを禁止したり、施設から締め出したりしたとしても、誰かに賭けをさせるのは簡単です。とはいえ、以前、プロギャンブラーのフェジックがスーパーボウルで行ったプロポジションベットのセミナーに行ったのですが、彼はハロウィーンのマスクをかぶってプレゼンテーションをしていました。
スーパーボウルのプールで最後の数字を選ぶためのアドバイスはありますか?
私が見たオフィスプールでは、各行と各列にランダムな数字を割り当てることで表をランダム化していました。しかし、実際に末尾の数字を選択できる場合は、次の表は1983年から2003年までのNFLの全試合に基づいて、両チームの最終スコアにおける各末尾の数字の出現頻度を示しています。
NFL 片側ターミナル数字
桁 | 頻度 | 確率 |
0 | 1887 | 17.75% |
1 | 1097 | 10.32% |
2 | 348 | 3.27% |
3 | 1382 | 13.00% |
4 | 1608 | 15.13% |
5 | 396 | 3.73% |
6 | 848 | 7.98% |
7 | 1945 | 18.30% |
8 | 631 | 5.94% |
9 | 488 | 4.59% |
合計 | 10630 | 100% |
したがって、この表では 7 が最適な選択であり、次に 0、4、3 が続くことがわかります。
いくつかは特に気に入っています。私のモデルは、各試合で公平なスプレッドを推定し、その差が一定以上の試合をリストアップしています。個人的には、差が大きい試合に賭けることが多いです。しかし、私の予想が本当に正しいと証明されるまでは、自信の度合いを公表するのはおこがましいと思っています。
NFL のピックに関しては、すべて同じ重み付けになっていますか? つまり、モデルによれば、ピックのうちのどれかが他のピックよりも強いのでしょうか?
いくつかは特に気に入っています。私のモデルは、各試合で公平なスプレッドを推定し、その差が一定以上の試合をリストアップしています。個人的には、差が大きい試合に賭けることが多いです。しかし、私の予想が本当に正しいと証明されるまでは、自信の度合いを公表するのはおこがましいと思っています。
あなたは心からパッカーズファンですか? ええ、そうです。あなたは心で賭けているようですが、パッカーズはあなたの素晴らしいNFL予想を台無しにしていますね。パッカーズが期待に応えられなかったとしても、素晴らしい確率ですね。この意見があなたにも気に入ってもらえるかと思いました。
理由はチームへの忠誠心とは全く関係ありません。私のプログラムでは、2004年シーズン終了時点で彼らを5番目に優れたチームと評価し、そのパワー評価を2005年シーズンにも引き継いでいます。しかし、最近の状況に反応するには遅すぎるのかもしれません。これは私にとっても考えるべき点です。
100試合以上でスプレッドに対して57%のオッズを持つプレイヤーに対して、2-1のオッズを提示している人を見ました。57%という数字は厳しいと思いますが、サンプル数が少ないことを考えると、良い賭けになるかもしれません。質問なのですが、もしベッターが生涯オッズ50%のオッズを持つプレイヤーで、ヴィグとタイ(つまりコイントスの状況)を無視した場合、これは良い賭けになるでしょうか?もしそうでない場合、オッズ全体のオッズがどの程度であれば、オッズをオッズするプレイヤーにとって良い取引になるでしょうか?
2対1のベットの場合、このベットが有効な最大サンプル数は14試合です。ランダムに選んだ場合、57%以上の的中率、つまり8回以上的中する確率は39.5264%です。有効なベットとなるには、33.3333%以上の確率が必要です。21回は妥当な数字ですが、確率は33.1812%とやや低すぎます。必要な選択数が多いほど、必要な割合は低くする必要があります。例えば、1000回の選択が必要な場合、勝率が1/3を超えるために必要な最大数は507です。1000回の選択で507回以上的中する確率は34.05%です。
私は長年のサッカーファンであり、ギャンブラーでもあります。あなたのサッカーの数値モデルにとても興味があり、自分の知識だけではサッカー賭博で勝てないことは既に分かっているので(試してみたのですが)、独自のモデルを作ろうとしています。そこで、統計的なアプローチを試してみようと思い立ちました。統計プログラムはSPSSを使用しています。質問なのですが、あなたのモデルではどのような変数を使用していますか?
モデルに入力するのはスコアとホームフィールドアドバンテージだけです。第6週のベン・ロスリスバーガーの負傷や、ニューオーリンズがサンアントニオでホームゲームを行うなど、大きな怪我については外部の意見を求めることもあります。
ウィザードさん、おかえりなさい。あなたはもはやオッズのウィザードであるだけでなく、そのパフォーマンスから判断すると、 NFLピックのウィザードでもあると言えるでしょう。カジノプールでの私の予想はたったの51.7%です。お願いがあります。もしお時間をかけずによろしければ、毎週全試合の予想をリストアップしていただけますか?
ありがとうございます。おそらく4週目になる前に送っていただいたのでしょう。4週目は私にとっては良くない週でした。5週間経った今、私の成績は17勝13敗で平均勝率は56.7%です。まあまあ良い方ですが、最高とは言えません。ニュースレターの読者への特典として、全試合の感想をお伝えしようと思います。
まず、この賭けを受け入れた者は誰であれ、原則としてそれを守るべきです。紳士は借金、特にギャンブルの借金を返済します。次に、私はまだ研究していませんが、クォーター間の相関関係は実際には逆相関しているのではないかと考えています。例えば、第1クォーターの合計得点が低い場合、どちらのチームも第2クォーター開始時に有利なフィールドポジションを確保し、第2クォーターで高得点を獲得する可能性が高くなるでしょう。逆もまた同様です。
ウィザードさん、 NFLの予想における私の「本当の」勝率について質問があります。私は友人たちに、過去5年間負けシーズンは一度もなかった(これは本当です)と言っています。3週目から16週目まで、毎週平均2~3回賭けています。私の強みは、試合の感覚が鋭く、オッズが自分に有利だと思う試合には、かなり多く賭けることです。例えば、今年は9回賭けて、そのうち4回は55ドルで、そのうち3回は的中しました。110ドルの賭けも3回して、そのうち1回は勝ちました。しかし、330ドルと600ドル(イーブンライン)を賭けた2試合は、どちらも勝ちました。確かに、9回中6回は66%の勝率ですが、より確信を持って予想した試合で的中しているので、実際には約80%の勝率(金額的には)ということになります。この説明は納得できますか?過去5年間の計算で、大体この通りでした(予想では60~70%ですが、賭けた金額を考慮すると約80%です)。賭け金を考慮する簡単な方法と、私の仮定が正しいかどうかを教えてください。どうもありがとうございます。
最近、このことについてよく考えます。勝率は試合ごとに均等に配分されるべきだと私は考えています。また、全体的な投資収益率についても別途統計を取るべきですが、どのような統計も、サイド、日付、ラインソース、ポイントスプレッド、そしてオッズ(通常は-110)のリストで裏付けられるべきです。あなたが触れていないもう一つの問題は、3ポイントまたは7ポイントスプレッドで-120のオッズを賭けなければならない場合の対処法です。そのような賭けをピックに多く含めれば、高い勝率を達成しやすくなります。ですから、フラットベッティングの場合でも、投資収益率は維持すべきだと私は考えています。他のハンディキャッパーについて私が気になっているもう一つの点は、どこにも見当たらないラインを引用することです。多少は比較検討するのは構わないと思いますが、引用されているラインを見つけるのは難しくないはずです。私自身、今シーズンはこれらのことをいくつか行っていないことを認めます。なぜなら、始めた頃にはこれらのことを考えていなかったからです。来年、これをもう一度やるなら、投資としての結果も記録しておきます。
賭けをする理由に関係なく、一般的には、マネーラインではアンダードッグに賭け、スプレッドではフェイバリットに賭ける方が良いでしょう。
NFLのハンディキャッピングを自分でやってみたいとずっと思っていましたが、チーム別の過去のデータをダウンロードできるサイト(できれば無料)がなかなか見つかりません。何か良いアイデアはありますか?ウェブページから切り取って貼り付けるのは現実的ではないので、ダウンロード可能なファイルがあれば嬉しいですが、必要であればそうしても構いません。また、天候や芝の状態などの情報も教えていただけると大変助かります。
個人的には、 Mr. NFLのNFL Accessデータベースを使っています。これは99ドルです。これより安くて同等の機能を持つものがあるかどうかは、私には分かりません。
歴史的に見て、アンダードッグの方がより良い賭けと言えるでしょう。1983年シーズン開幕から2005年シーズン第10週までの全試合の結果はこちらです。
スプレッドに対するフェイバリットの勝利数: 2554試合
アンダードッグがスプレッドに勝利:2724試合
ゲームはスプレッドで終了:150ゲーム
つまり、決着がついた賭けでは、アンダードッグが51.61%の確率で勝利していることになります。また、スクエアベッターはフェイバリットに賭けることを好むため、アンダードッグにバリューが生まれることもよく知られています。
今年、私たちの「フットボールベットテイカー」はオーバー/アンダーベットのジュースを10%から20%に引き上げ、パーレイの10%ジュースを廃止しました。そのため、今年はオーバー/アンダーベットを2つ別々に行う代わりに、2つのベットを2.5対1の配当でパーレイしています。これは良い戦略でしょうか?
ストレートベットの期待リターンは(0.5*1 + 0.5*(-1.2))/1.2 = -8.33%です。パーレーベットの期待リターンは0.25*2.5 + 0.75*-1 = -12.5%です。しかし、もし2試合だけ賭けて、勝つか負けるかのどちらかだけを狙うなら、パーレーベットを選びます。さらに重要なのは、このブックメーカーは原則としてボイコットするということです。なぜなら、ストレートベットで-120のオッズを賭けなければならないなんて聞いたことがないからです。
貴サイトの2つのセクションで、マネーラインでは一般的にフェイバリットよりもアンダードッグに賭ける方が良いと述べられています。しかし、スポーツベッティングの付録3で指摘されているように、フェイバリットに賭けた場合、マネーラインのハウスエッジは低くなります。これは矛盾ではないでしょうか?どんな賭けでも、ハウスエッジが最も低いものを目指すべきではないでしょうか?
いい指摘ですね。よく考えた結果、スポーツベッティングに関する付録3を削除することにしました。この付録は、フェアラインは2つのマネーラインのちょうど中間にあるという仮定に基づいていました。例えば、前回のスーパーボウルでは、マネーラインは概ねシアトルが+160、ピッツバーグが-180でした。私の付録は、フェアラインは+/- 170になるという非現実的な仮定に基づいていました。実際には、マネーラインは市場によって決まります。マネーラインのスクエアアクションはフェイバリットに有利に働く傾向があり、アンダードッグにバリューを生み出します。ピッツバーグが4ポイントのフェイバリットだと仮定すると、過去のデータによると、4ポイントのフェイバリットが勝つ確率は約61%です。そうすると、フェアラインはシアトルで+156、ピッツバーグで-156になります。ちなみに、ほとんどのカジノのマネーラインは+160/-180でした。もちろん、今回はピッツバーグが勝利しましたが、歴史的に見れば、マネーラインで優勝候補より劣勢チームに賭けたほうが得策であることは間違いありません。
NFLスクエアプールに参加しているのですが、とても良い数字を引きました。ピッツバーグが7対4、シアトルが4対0です。今年私が勝つ確率はどれくらいでしょうか?
質問を理解できない読者のために説明すると、スーパーボウルのプールには 10 x 10 のグリッドがあります。プレーヤーはそれぞれ一定額のマスを購入し、各マスに購入者の名前を書きます。100 個のマスがすべて購入されたら、行と列に 0 から 9 までの見出しがランダムに付けられます。10 x 10 の掛け算表のようなものですが、行と列の見出しがランダムにシャッフルされます。その後、各チームのスコアの最後の数字を使用して勝者を決定します。シャッフルする理由は、以下に示すように、一部の最後の数字が他の数字よりも可能性が非常に高いためです。たとえば、シアトル 0、ピッツバーグ 1 のマスを手に入れたチームがプールの勝者になります。最終スコアはシアトル 10、ピッツバーグ 21 だったからです。
以下の表は、1983年から2005年シーズンのNFL全試合における各組み合わせの出現頻度を示しています。2ポイントコンバージョンルールは1998年頃に導入されたため、分布がやや平滑化されている点に留意してください。
NFLの終値 - アウェイとホームの合計
| アウェイチーム | ホームチーム | 合計 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 126 | 104 | 34 | 160 | 138 | 37 | 99 | 237 | 64 | 32 | 1031 |
| 1 | 73 | 40 | 17 | 41 | 103 | 21 | 36 | 117 | 67 | 31 | 546 |
| 2 | 25 | 15 | 1 | 20 | 30 | 9 | 13 | 33 | 9 | 12 | 167 |
| 3 | 194 | 69 | 33 | 66 | 102 | 40 | 102 | 132 | 43 | 40 | 821 |
| 4 | 122 | 133 | 27 | 78 | 108 | 27 | 48 | 215 | 59 | 35 | 852 |
| 5 | 32 | 12 | 12 | 21 | 21 | 9 | 13 | 36 | 22 | 5 | 183 |
| 6 | 91 | 47 | 17 | 75 | 57 | 7 | 28 | 57 | 25 | 39 | 443 |
| 7 | 217 | 115 | 35 | 135 | 195 | 47 | 65 | 125 | 69 | 47 | 1050 |
| 8 | 43 | 59 | 12 | 24 | 41 | 23 | 20 | 38 | 15 | 7 | 282 |
| 9 | 48 | 28 | 17 | 33 | 40 | 14 | 29 | 33 | 14 | 7 | 263 |
| 合計 | 971 | 622 | 205 | 653 | 835 | 234 | 453 | 1023 | 387 | 255 | 5638 |
次の表は、上の表の合計に基づいた各組み合わせの確率を示しています。
NFLのターミナルディジット - アウェイバイホームの確率
| アウェイチーム | ホームチーム | 合計 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0 | 0.0223 | 0.0184 | 0.006 | 0.0284 | 0.0245 | 0.0066 | 0.0176 | 0.042 | 0.0114 | 0.0057 | 0.1829 |
| 1 | 0.0129 | 0.0071 | 0.003 | 0.0073 | 0.0183 | 0.0037 | 0.0064 | 0.0208 | 0.0119 | 0.0055 | 0.0968 |
| 2 | 0.0044 | 0.0027 | 0.0002 | 0.0035 | 0.0053 | 0.0016 | 0.0023 | 0.0059 | 0.0016 | 0.0021 | 0.0296 |
| 3 | 0.0344 | 0.0122 | 0.0059 | 0.0117 | 0.0181 | 0.0071 | 0.0181 | 0.0234 | 0.0076 | 0.0071 | 0.1456 |
| 4 | 0.0216 | 0.0236 | 0.0048 | 0.0138 | 0.0192 | 0.0048 | 0.0085 | 0.0381 | 0.0105 | 0.0062 | 0.1511 |
| 5 | 0.0057 | 0.0021 | 0.0021 | 0.0037 | 0.0037 | 0.0016 | 0.0023 | 0.0064 | 0.0039 | 0.0009 | 0.0325 |
| 6 | 0.0161 | 0.0083 | 0.003 | 0.0133 | 0.0101 | 0.0012 | 0.005 | 0.0101 | 0.0044 | 0.0069 | 0.0786 |
| 7 | 0.0385 | 0.0204 | 0.0062 | 0.0239 | 0.0346 | 0.0083 | 0.0115 | 0.0222 | 0.0122 | 0.0083 | 0.1862 |
| 8 | 0.0076 | 0.0105 | 0.0021 | 0.0043 | 0.0073 | 0.0041 | 0.0035 | 0.0067 | 0.0027 | 0.0012 | 0.05 |
| 9 | 0.0085 | 0.005 | 0.003 | 0.0059 | 0.0071 | 0.0025 | 0.0051 | 0.0059 | 0.0025 | 0.0012 | 0.0466 |
| 合計 | 0.1722 | 0.1103 | 0.0364 | 0.1158 | 0.1481 | 0.0415 | 0.0803 | 0.1814 | 0.0686 | 0.0452 | 1 |
スーパーボウルにはセレモニーホームチームがありますが、これは無視して構わないと思います。両チームに関するすべての情報も無視し、上記の過去の平均値のみに基づいて考えてみましょう。最後に、スーパーボウルは引き分けにならないという事実も無視しましょう。引き分けの場合、4/4のような試合の勝率は少し低くなります。そこで、末尾の数字が異なる場合の平均を取りましょう。例えば、ピッツバーグ7、シアトル4のマスの確率は、アウェイ7、ホーム4とアウェイ4、ホーム7の平均になります。こうすることで、各マスの確率は次のようになります。
ピッツ 7、シー 4: (0.0346+0.0381)/2 = 0.0364
ピッツ 7、シー 0: (0.0385+0.0420)/2 = 0.0403
ピッツ 4、シー 4: 0.0192
ピッツ 4、シー 0: (0.0216+0.0245)/2 = 0.0231
つまり、これらのうち1つに当たる確率は合計で11.90%です。ただし、うまくできたマス目はわずか4%しかカバーできていないことを考慮すると、この確率は高くなります。
特にご質問はございませんでしたが、各末尾の数字の出現頻度は以下のとおりです。全体的に見て、最も頻繁な順序は7043168952です。
NFLの終値 — アウェイとホームの合計
| ターミナル 桁 | アウェイチーム | ホームチーム | 合計 |
|---|---|---|---|
| 0 | 1031 | 971 | 2002 |
| 1 | 546 | 622 | 1168 |
| 2 | 167 | 205 | 372 |
| 3 | 821 | 653 | 1474 |
| 4 | 852 | 835 | 1687 |
| 5 | 183 | 234 | 417 |
| 6 | 443 | 453 | 896 |
| 7 | 1050 | 1023 | 2073 |
| 8 | 282 | 387 | 669 |
| 9 | 263 | 255 | 518 |
最後に、各末尾の数字の確率を示します。
NFLの終値 — アウェイとホームの確率
| ターミナル 桁 | アウェイチーム | ホームチーム | 合計 |
|---|---|---|---|
| 0 | 0.1829 | 0.1722 | 0.1775 |
| 1 | 0.0968 | 0.1103 | 0.1036 |
| 2 | 0.0296 | 0.0364 | 0.033 |
| 3 | 0.1456 | 0.1158 | 0.1307 |
| 4 | 0.1511 | 0.1481 | 0.1496 |
| 5 | 0.0325 | 0.0415 | 0.037 |
| 6 | 0.0786 | 0.0803 | 0.0795 |
| 7 | 0.1862 | 0.1814 | 0.1838 |
| 8 | 0.05 | 0.0686 | 0.0593 |
| 9 | 0.0466 | 0.0452 | 0.0459 |
このトピックの詳細については、 「Football Squares の数学的および統計的戦略」をご覧ください。
ラスベガスのスポーツベッティングの上限額は非常に高いという誤解をされている方がいらっしゃいますが、私の経験では、これはフットボールにのみ当てはまり、必ずしもそうとは限りません。ラスベガスのスポーツブックにおける主要4スポーツの上限額はどれくらいでしょうか?お時間をいただき、ありがとうございます。
ホッケーは試合数が少ないので、メジャースポーツとは考えていません。海岸沿いのカジノは賭け金の上限が最も高いと聞いています。私の知る限り、上限額は決まっていませんが、ケースバイケースで高額の賭けを受け付けています。平均的な試合では、おそらくこのくらいの金額が適用されると思います。
NFL側:5万ドル
NFL総額:5000ドル
MLBマネーライン:1万ドル
MLB合計:2000ドル
NBA側:1万ドル
NBA合計:2,000ドル
多くのオンラインブックメーカーがハーフタイムベッティングを提供していますが、「ダッチング」についてあなたの意見をぜひお聞かせください。当たり前のことかもしれませんが、ハーフタイムに試合の賭け金の反対に賭けることを検討するのは、どの時点でしょうか?また、有利な状況になった場合、どの程度の金額を検討しますか?
「ダッチング」とはヘッジのことでしょうか。私のギャンブルにおける十戒の6番目は「汝、賭けをヘッジするなかれ」です。例外を設けるのは、ヘッジベット自体の期待値がプラスの場合、あるいは人生を変えるほどの金額が賭けられている場合だけです。
ラスベガスのカジノで大学フットボールの賭けをした場合、チケットを換金する際に個人情報を提供せずに、最高いくらまで勝ち取ることができるでしょうか? 質問なしで現金を受け取れる金額(賭け金1回あたり)を知りたいです。
10,000ドル。スポーツ賭博に限らず、10,000ドルを超える現金取引にはCTR(現金取引報告書)が必要です。チップでの支払いを依頼することもできますが、換金した場合でも同じCTRが発生します。
無料サイト以外で、月額料金または勝率でプロのスポーツハンディキャップを取得できるサイトをお勧めいただけますか。
いいえ。私はいかなる客引きも支持しません。
NFLのアンダードッグへの賭けについてお話いただきましたが、毎回ホームチームのアンダードッグに賭けていたのですか?それとももっと複雑な賭け方だったのですか?そして最も重要なのは、ホームチームのアンダードッグかどうかはどのラインで決まるのでしょうか?試合開始前のラインですか?それとも試合直前のラインですか?ありがとうございます。
今シーズン、ラスベガスのダウンタウンにあるプラザ・ホテルでは、たとえ-105ドルしか賭けられなかったとしても、私は盲目的にアンダードッグに賭けることはありません。スポーツベットでわずかなアドバンテージしか感じられなければ、賭けません。スポーツでは、常にある程度の誤差を前提としています。なぜなら、最終的には統計ではなく、人間が試合をするからです。しかし、市場よりも良いオッズを見つけたり、信頼できるハンディキャッパーの推奨があれば、喜んで賭けます。
素晴らしいウェブサイトをありがとうございます!父とヘッジベットについて言い争いになっていて、本当に助けていただきたいです!具体的な状況はスーパーボウルの賭けです。シーズン開幕前(父はシーズン開始年を覚えていません)、叔父はニューイングランドがスーパーボウルで優勝すると賭けました。配当は60倍でした。スーパーボウル(ニューイングランドが出場)の直前、叔父はヘッジベット(父は詳細を覚えていません)を行い、6,000ドルの賞金を諦めて代わりに3,000ドルの賞金を確保しました。私はこれが愚かな賭けだったと確信していますが、父は私の言うことを聞きません。このヘッジベットは期待値を放棄することになり、賢い賭け手は決してそんなことはしない、と主張しています。父は、金額が絡んでいることと、この賭けはめったに起こらないこと、まさに家の保険をかけるのと同じことだから、期待値を放棄しても問題ないと主張しています。もちろん、住宅所有とスポーツ賭博は本質的に異なると私は考えています。前者は避けられますが、後者は避けられないからです。皆さんはどうお考えですか?この件の解決にご協力ください!
私のギャンブル十戒の7番目は「賭けをヘッジするなかれ」です。しかし、私はその発言の中で、「人生を変えるほどの金額を保険でカバーする場合は例外を認める」と付け加えています。ですから、もし3,000ドルの解約返戻金が彼にとって人生を変えるほどの金額であり、当選確率が50%をわずかに上回る程度であれば、私は彼の決断を咎めるつもりはありません。しかし、これが2002年でない限り、ニューイングランドの優勝確率は50%をはるかに上回っていました。彼らがスーパーボウルに出場した他の2年間、2004年と2005年には、7ポイントの優勢でした。どちらの年も優勝確率は約71%と推定されます。妥当な解約返戻金は、0.71 × 6,100ドル(彼の当初の賭け金を含む)=4,331ドルだったでしょう。このオファーのハウスエッジは、相手チームに賭けるのと同額で、29%-71% = 42%でした。つまり、もし私がその年の予想を正しければ、彼は非常に誤った判断をしたことになります。マネーラインで相手チームに賭ければ、オープンマーケットでずっと良いオッズを得ることができたはずです。たった3,000ドルしかオファーしなかった人は、このスポーツについて全く無知だったか、不当に有利な立場にいたかのどちらかです。興味深いことに、ニューイングランドは最近のスーパーボウル3回全てで3点差で勝利しています。
NFL の試合が引き分けで終わる確率はどれくらいでしょうか?
1983年から2007年のシーズンでは、レギュラーシーズン5,901試合中、引き分けは10回ありました。ポストシーズンでは引き分けにならないことがルールで定められています。したがって、過去の試合に基づくと、引き分けの確率は0.17%、つまり約590試合に1試合となります。
NFL の試合における 2 つのチームの最終的な得点差とその試合のポイントスプレッドの差の標準偏差はどれくらいでしょうか?
他の読者のために、前回のスーパーボウルの例で、あなたの質問の意味を説明しましょう。ペイトリオッツは12点の優勢でしたが、3点差で敗れました。つまり、試合は得失点差から15点差で終了しました。質問を正しく理解していれば、この差の標準偏差についてお尋ねだと思います。調査した各リーグの平均差はほぼゼロでした。標準偏差は以下のとおりです。
NFL 13.31(2000年から2007年のシーズンに基づく)
カレッジフットボール 15.72(1993年から2007年のシーズンに基づく)
NBA 11.39(1987年から2003年のシーズンに基づく)
つまり、2008年のスーパーボウルは、予想から15/13.31 = 1.13標準偏差離れた結果となりました。ここでは、できるだけ単純化するために離散分布の調整係数は無視しています。予想から1.13標準偏差以上離れる確率は、どちらの方向でも25.85%です。これはExcelで、2 × normsdist(-1.13)という式を使って計算できます。
スポーツベッターとして、アンダードッグに賭けるのが好きで、ラインをあれこれ検討するのが好きなので、少しでも多くのハーフポイントを獲得することの価値を知っています。NFLやNBAの試合で、あなたにとってハーフポイントはどれくらいの価値がありますか?フェアラインで-110のギャンブラーが損益分岐点に達するには、52.4%の的中率が必要だと知っています。ラインは市場によって決まることは知っていますが、ハーフポイントの本当の価値はどれくらいだと思いますか?賭ける試合ごとにフェアラインでハーフポイントを追加で獲得できたとしたら、損益分岐点は本当に50%になるのでしょうか?計算方法はありますか?ありがとうございます。
質問ではないのですが、120をレイする場合、ほとんどのスポーツブックではハーフポイントを購入できます。もしスプレッドに賭けるつもりなら、追加のハーフポイントはお得でしょうか?110をレイする場合、ランダムピッカーのハウスエッジはタイを含めて4.45%です。120をレイする場合、ハーフポイントのハウスエッジは4.50%です。つまり、ハーフポイントを購入するのは、価格に見合う価値がほとんどないということです。
フットボールでハーフポイントを購入する価値は、ポイントスプレッドに大きく左右されます。なぜなら、勝利の確率は、あるポイントスプレッドと他のポイントスプレッドで大きく異なるからです。NFLでハーフポイントを購入する価値があるのは、ポイントスプレッドが3の場合のみです。残念ながら、スポーツブックもこのことを知っており、ほとんどの場合、3の場合はハーフポイントの購入を許可しません。
チーム A は平均して 1 試合あたり 1.5 ゴール、チーム B は平均して 1 試合あたり 1.2 ゴールを獲得するとします。A と B の間の試合で次の可能性はどれくらいでしょうか。
1) AはBよりも高い得点を獲得する
2) BはAよりも高い得点をあげる
3) ゲームは引き分けで終了します。
提供された情報は、それぞれの結果の確率を計算するのに十分ですか?
ただし、個々の得点は多少負の相関関係にあるはずであり、各チームが失う平均得点は平均得点と同じくらい重要であるという点を考慮していません。攻撃と守備の両方を考慮し、試合で期待される得点数を1.5点と1.2点と仮定し、相関係数を無視すれば、3つの確率をある程度推定できます。このようなスーパーボウルのプロップは数多くありますが、タッチダウン、フィールドゴール、インターセプトなどを誰がより多く決めるかに基づいています。
最初のステップは、ポアソン分布を用いて各チームのゴール数ごとの確率を推定することです。一般的な公式は、チームが平均mのゴール数gを獲得する確率は、e -m × m g /g!です。Excelでは、poisson(g,m,0)という式を使用できます。次の表は、この式を用いて両チームのゴール数が0から10までの確率を示しています。
各チームの0~8ゴールの確率
| 目標 | チームA | チームB |
| 0 | 0.223130 | 0.301194 |
| 1 | 0.334695 | 0.361433 |
| 2 | 0.251021 | 0.216860 |
| 3 | 0.125511 | 0.086744 |
| 4 | 0.047067 | 0.026023 |
| 5 | 0.014120 | 0.006246 |
| 6 | 0.003530 | 0.001249 |
| 7 | 0.000756 | 0.000214 |
| 8 | 0.000142 | 0.000032 |
次のステップはやや地味ですが、各チームの0から8までのスコアの81通りの組み合わせ全てをマトリックスにまとめる必要があります。これは、上の表にあるチームAのスコアxとチームBのスコアyの確率を掛け合わせることで行います。次の表は、0-0から8-8までのすべてのスコアの組み合わせの確率を示しています。
次の表は、ゴールの組み合わせごとに勝者を示しています。T は引き分けを表します。
両チームの勝利の組み合わせ
| ゴールチームA | ゴールチームB | ||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | T | B | B | B | B | B | B | B | B |
| 1 | あ | T | B | B | B | B | B | B | B |
| 2 | あ | あ | T | B | B | B | B | B | B |
| 3 | あ | あ | あ | T | B | B | B | B | B |
| 4 | あ | あ | あ | あ | T | B | B | B | B |
| 5 | あ | あ | あ | あ | あ | T | B | B | B |
| 6 | あ | あ | あ | あ | あ | あ | T | B | B |
| 7 | あ | あ | あ | あ | あ | あ | あ | T | B |
| 8 | あ | あ | あ | あ | あ | あ | あ | あ | T |
最後に、Excelのsumif関数を使って、賭けの3つの可能な結果すべてに対応するセルを合計します。この場合の確率は次のとおりです。
Aが勝つ = 44.14%
Bの勝利 = 30.37%
同点 = 25.48%
スタンフォード・ウォン著『シャープ・スポーツ・ベッティング』の付録Cには、このような賭けにおける勝敗や引き分けの確率が示されています。このケースでは、44%、30%、25%とされています。このような問題を解く簡単な公式をご存知の方がいらっしゃいましたら、ぜひ教えてください。
追記:数学のこととなるといつも私を刺激してくれるボブ・Pさんからメールをいただきました。内容は以下のとおりです。
2つの無相関ポアソン分布の差の分布を調べました。これはスケラム(私にとっては新しい)です。いずれにせよ、質問は P(Z=0)、P(Z>0)、および P(Z<0) として提示されます。ここで、Z はパラメータ 1.5 と 1.2 を持つ Skellam です。
まだやっていないなら、知っておくと喜ばれるでしょう
P(同点) = P(Z=0) = .254817
P(AがBに勝つ) = P(Z>0) = .441465
P(BがAに勝つ) = P(Z<0) = 1 - .254817 - .441465 = .303718
ほぼあなたの答え通りです。
スケラムのWikipediaの項目にはベッセル関数について触れられていましたが、微積分学ではそのあたりでこれ以上先に進むのが怖くなってしまいました。なので、今回はボブの言葉を信じることにします。
5連敗しているチームに賭けても、5連勝しているチームに賭けても、良い結果が出てきました。サイコロやルーレットのように、サイコロやボールに記憶力がないと言われるのとは異なり、プロスポーツのチームは永遠に勝ち続けたり負けたりはしない、というのが私の考えです。5連勝を選んだのは、いつチームが入れ替わるかを分析したからです。試合の開催場所や先発投手、怪我の状況などは、私にとっては関係ありません。私の考えは正しいと思いますか?
これらは良い賭けだと思いますが、あなたが挙げた理由とは違います。スポーツチームは理論上、延々と負け続ける可能性があります。そもそもこれらが良い賭けである理由の一つは、ほとんどの場合、大方の予想を覆すアンダードッグに賭けられることであり、アンダードッグは一般的にフェイバリットよりも有利な賭けです。もう一つの理由は、スクエアベッターはこのような状況では逆の方向に賭ける傾向があり、あなたの主張する方向に価値を生み出しているからです。
NFLのハンディキャップコンテストに参加している6人のうちの1人です。私たちはそれぞれ、シーズンを通して70試合を、大手インターネットスポーツブックの20セントラインのラインを基準に予想しなければなりません。他の参加者の1人は、シーズン終了時の最高スコアにオーバー/アンダーのプロップベットを提供しました。彼のラインは8.5ユニットの利益でした。シーズンはまだ始まっておらず、参加者は経験豊富なスポーツベッターだと仮定しましょう。あなたはそのラインについてどう思いますか?また、どのように分析しますか?
このようなプロップで自問自答すべき大きな疑問は、特定のピックが勝ち、負け、またはプッシュで終わる確率はどれくらいかということです。私のNFL ベッティングのセクションから、2.8% の試合がラインぎりぎりで終わることがわかります。簡単にするために 3% としましょう。賭けが決着した場合の勝利の確率を p としましょう。完全にランダムに選ぶ場合、p は明らかに 50% になります。アンダードッグだけを選ぶことで、この値を簡単に改善できます。前述のページが示すように、25 シーズン以上アンダードッグにフラットベットすると、勝率は 51.5% になります。また、市場全体に対して最も弱いラインを厳選することで、この値をもう少し改善することも簡単です。この 2 つを合わせれば、52% に到達するのは難しくないと思います。ですから、これらの人たちは少なくとも 52% までは到達できると信じて受け入れることにします。
したがって、解決された賭けの 52% が勝つと仮定すると、全体的な確率は次のようになります。
勝率: 50.44%
引き分け: 3.00%
損失: 46.56%
基本的な統計を用いると、-110のレイイングで1ピックあたりの期待勝利額は-0.0078であることが容易に分かります。1ピックあたりの標準偏差は1.0333です。70ピックでの期待勝利額は-0.5432で、標準偏差は70 1/2 × 1.0333 = 8.6452です。8.5ユニットの勝利は期待値より9.0432ユニット高く、ガウス曲線上で期待値の右側に9.0432/8.6452=1.0460標準偏差あります。プッシュや-110/-110ではない試合もあるため、離散分布の調整は無視できると思います。0.05ユニットの係数でかなり滑らかな曲線になるでしょう。
したがって、いずれかの選手が期待値を1.046標準偏差以上上回る確率は14.77%です。この数値はガウス曲線の表、またはExcelの式 =1-normsdist(1.046) で求めることができます。6人の選手全員が1.046標準偏差以下で終了する確率は (1-0.1477) 6 =38.31%です。したがって、少なくとも1人の選手が1.046標準偏差以上で終了する確率は61.69%です。つまり、オーバーは-110の堅実な賭けのように見えます。-161であれば妥当な賭けだと示します。
以下の表は、pの様々な値における8.5以上のオッズが勝つ確率を示しています。おそらく、このプロップを設定した人はpの値を51%に近い値と想定していたのでしょう。
NFLハンディキャッププロップ
| おそらく正しい選択 | おそらくオーバー勝利 |
| 50.0% | 41.16% |
| 50.5% | 46.18% |
| 51.0% | 51.33% |
| 51.5% | 56.53% |
| 52.0% | 61.69% |
| 52.5% | 66.72% |
| 53.0% | 71.52% |
ペイトリオッツが自陣28ヤードラインで4thダウン、しかも6点リードしている状況で1stダウンを狙うという判断についてどう思いますか?あの状況で1stダウンを獲得できる確率はどれくらいですか?あなたならどうしますか?
他の読者のために補足すると、これは2009年11月15日の試合のことを指しています。ペイトリオッツはコルツに6点リードしていました。第4クォーター残り1分57秒、フォースダウン、残り約1.5ヤード、ボールはペイトリオッツの28ヤードラインにありました。ペイトリオッツのビル・ベリチック監督は、結果を先送りしてパントするのではなく、フォースダウンショートでファーストダウンを狙うという、今では物議を醸している決断を下しました。
これについて、ラスベガス・レビュー・ジャーナル紙に良いコラムが掲載されています。プロのギャンブラーであり、同じくアクチュアリーでもあるスティーブ・フェジック氏が、ファーストダウンを狙う方がオッズが有利だと述べています。私も全く同感です。一般的に、他のコーチはパントをしすぎ、リスクを取ることを恐れすぎていると思います。私の立場を裏付けるために、数学が得意でスポーツベッターでもあるジョエル・B氏に尋ねました。彼は試合中のフットボールのオッズ分析が私よりはるかに得意です。彼は次のようなオッズを提示しました。
- ペイトリオッツがファーストダウンを獲得する確率:60%
- ペイトリオッツがファーストダウンを獲得した場合の勝利確率:100%
- ペイトリオッツがファーストダウンを逃した場合の勝利確率:50%
- パントした場合のペイトリオッツの勝利確率:75%
つまり、ファーストダウンを狙う場合の勝率は、60%×100% + 40%×50% = 60% + 20% = 80%となります。これはパントした場合の勝率75%よりも高いです。
月曜朝のクォーターバックたちはいくらでもベリチックを非難できるだろうが、私は彼の決断を称賛する。彼は試合の結果ではなく、当時の彼の行動がオッズに有利だったかどうかで判断されるべきだ。私はオッズが有利だったと強く思う。1週間後のレイブンズ対スティーラーズの試合では、レイブンズは4ダウン5ヤードでトライし、そして成功した。状況は違ったが、あの決断を疑問視する声はまだ聞いたことがない。
公平を期すために、私はESPN.comのビル・シモンズによる「ベリチックの4回目の無謀なプレー」というタイトルの反対の視点の記事へのリンクを提供します。
選手が有利だと思うサッカーの試合が2つあるとします。それぞれの勝率が55%で、110を賭けなければならないとします。ストレートアップで賭けるのと、シングルパーレーで賭けるのとでは、どちらが儲かるでしょうか?
いい質問ですね。単純に考えると、賭け金1回あたりのアドバンテージは0.55×(10/11) - 0.45 = 0.05です。パーレーにすると、アドバンテージは(0.55) 2 ×((21/11) 2 -1)-(1-(0.55) 2 ) = 10.25%になります。つまり、アドバンテージを最大化するにはパーレーが最適な方法と言えるでしょう。
しかし、パーレーの場合、分散は大きくなります。ケリー基準に従う場合は、パーレーのために資金を守るために、より少ない賭け金で資金を守る必要があります。この例では、ストレートアップでの最適なケリーベットは、2つのゲームが重複する場合は資金の5.48%、最初のゲームが2番目のゲームに賭ける前に終了する場合は5.50%、パーレーの場合は3.88%です。賭け金にアドバンテージを掛けると、ストレートアップでは0.00275(5.50%のアドバンテージに基づく)、パーレーでは0.00397となります。したがって、パーレーの方が利益が大きくなります。
この種の質問に対する一般的なケースとして、3チーム、4チームのパーレー、そしてマネーラインベットも検討しました。すべてのベットに若干のアドバンテージがあると仮定すると、経験則として、各イベントの勝率が33%未満であれば、ストレートアップに賭けるべきです。各確率が33%から52%の間であれば、2チームパーレーに賭けるべきです。各確率が52%から64%の間であれば、3チームパーレーに賭けるべきです。各確率が64%を超える場合は、4チームパーレーに賭けるべきです。ストレートアップに賭ける場合、2チームパーレーでも3チームパーレーでも、どちらもほぼ同じくらいの利益が得られます。ただし、これも最初からアドバンテージがあるという前提です。
娯楽としてギャンブラーとしてハウス エッジに対抗する場合 (どのスポーツ ベッターがそれを認めるでしょうか?)、ストレートアップで賭けるとハウス アドバンテージが最小限に抑えられることを強調しておきます。
NFL で 2 ポイント コンバージョンを達成する確率はどれくらいですか?
2000年から2009年のNFLシーズン(2009年のポストシーズンを除く)では、2ポイントコンバージョンの失敗は567回、成功は318回でした。これに基づくと、成功確率は318/(567+318) = 35.9%となります。

この写真は、小規模で保守的なスポーツブックであるLeroy'sのフランチャイズで撮影されました。彼らは通常、最初にスプレッドを発表し、その後にトータルラインとマネーラインを発表します。
また、イースタンミシガン大学対セントラルミシガン大学の試合のように、23ポイントのスプレッドがある試合では、マネーラインを設定することは稀です。このような試合では正確なマネーラインを設定することが難しく、不均衡な展開になるリスクが高くなります。スプレッドの大きい試合でマネーラインに賭けるのに最適なカジノは、ヒルトンです。最後に、ポイントスプレッドが1または1.5のように非常に小さい場合、ほとんどのスポーツブックはマネーラインを一切設定しません。スプレッドに逆らって賭けても、おそらく同じ結果になるからです。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
スーパーボウルのスコアを正確に予想して、サイン入り著書をプレゼントするチャンスをいただき、ありがとうございます。しかし、期待値はかなり低いのではないでしょうか?当選確率は300分の1くらいだと思います。
確かな知識に基づいた推測をすれば、オッズはそれよりも高くなると思います。NFLの試合の正確な結果を予想するための私の基本戦略をご紹介します。
- 合計とスプレッドを使って、各チームの合計得点を推定します。例えば、スーパーボウルの合計得点を57、スプレッドを-5とすると、c=コルツの得点、s=セインツの得点となります。
(1)c+s=57
(2)c-5=s
式(2)を式(1)に代入すると、
c+(c-5)=57
2c-5=57
2c=62
c=31
s=31-5=26
ここで止まってしまうと、単一のチームでは到底獲得できないような得点が出てくることがあります。例えば、単一チームの合計得点が24点になる確率は6.5%ですが、25点になる確率はわずか0.9%です。下の表は、2000年から2009年のシーズンに基づく、単一チームの合計得点の確率を示しています。そこで、フィールドゴールとタッチダウンの現実的な組み合わせに基づいて、各チームの合計得点を推定してみましょう。 - 優勝候補が2つのフィールドゴールを蹴ると仮定します。
- 劣勢のチームがフィールドゴールを 1 回蹴ると仮定します。
- それぞれのフィールドゴールポイントを差し引きます。スーパーボウルの例では、コルツは25タッチダウン、セインツは23タッチダウンとなります。
- タッチダウンポイントを7で割ると、推定タッチダウン数が得られます。c=3.57 TD、s=3.29 TD
- 推定タッチダウン数を最も近い整数に丸めます。c=4、s=3。
- この方法に従うと、合計ポイントはc=(4×7)+(2×3)=34、s=(3×7)+(1×3)=24となります。
この方法を1983年から2009年シーズンの全6,707試合に適用すると、69試合で的中し、成功率は1.03%となります。最後に的中したのは、2009年第13週のタイタンズ対コルツ戦です。この試合のスプレッドはコルツが-6.5、トータルは46でした。スコアはタイタンズ17、コルツ27でした。
ある批評家は、両チームとも最も近い有意なチーム合計を選ぶ方が、より良いシンプルな戦略だと考えました。しかし、この方法では勝利数はわずか51で、勝率は0.76%でした。私としては、フィールドゴール2と1を強いチームと弱いチームに分けることが重要だと考えています。NFL2000-2009シーズンのチーム別総得点
| ワンチーム合計 | サンプルの合計 | 確率 |
| 0 | 93 | 1.75% |
| 1 | 0 | 0.00% |
| 2 | 0 | 0.00% |
| 3 | 148 | 2.79% |
| 4 | 0 | 0.00% |
| 5 | 2 | 0.04% |
| 6 | 114 | 2.15% |
| 7 | 210 | 3.96% |
| 8 | 9 | 0.17% |
| 9 | 76 | 1.43% |
| 10 | 316 | 5.96% |
| 11 | 9 | 0.17% |
| 12 | 49 | 0.92% |
| 13 | 289 | 5.45% |
| 14 | 238 | 4.49% |
| 15 | 55 | 1.04% |
| 16 | 170 | 3.21% |
| 17 | 373 | 7.03% |
| 18 | 33 | 0.62% |
| 19 | 92 | 1.73% |
| 20 | 368 | 6.94% |
| 21 | 234 | 4.41% |
| 22 | 64 | 1.21% |
| 23 | 218 | 4.11% |
| 24 | 347 | 6.54% |
| 25 | 47 | 0.89% |
| 26 | 103 | 1.94% |
| 27 | 282 | 5.32% |
| 28 | 159 | 3.00% |
| 29 | 52 | 0.98% |
| 30 | 127 | 2.39% |
| 31 | 242 | 4.56% |
| 32 | 23 | 0.43% |
| 33 | 57 | 1.07% |
| 34 | 164 | 3.09% |
| 35 | 76 | 1.43% |
| 36 | 27 | 0.51% |
| 37 | 68 | 1.28% |
| 38 | 108 | 2.04% |
| 39 | 11 | 0.21% |
| 40 | 21 | 0.40% |
| 41 | 62 | 1.17% |
| 42 | 31 | 0.58% |
| 43 | 6 | 0.11% |
| 44 | 24 | 0.45% |
| 45 | 33 | 0.62% |
| 46 | 1 | 0.02% |
| 47 | 7 | 0。13% |
| 48 | 28 | 0.53% |
| 49 | 15 | 0.28% |
| 50 | 1 | 0.02% |
| 51 | 5 | 0.09% |
| 52 | 7 | 0.13% |
| 53 | 0 | 0.00% |
| 54 | 2 | 0.04% |
| 55 | 1 | 0.02% |
| 56 | 4 | 0.08% |
| 57 | 1 | 0.02% |
| 58 | 1 | 0.02% |
| 59 | 1 | 0.02% |
| 合計 | 5304 | 100.00% |
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
NFLで第4クォーター前にオンサイドキックが成功する確率はどれくらいでしょうか?スーパーボウルでの動きは本当に素晴らしかったですが、セインツのヘッドコーチは彼の判断を裏付ける統計データを持っていたのでしょうか?それともただの勘だったのでしょうか?
advancedfootballanalytics.com の素晴らしい記事によると、オンサイドキックの成功率は歴史的に26%だそうです。しかし、ほとんどのオンサイドキックは相手チームがそれを予期しているため、成功率は低くなります。一方、サプライズオンサイドキックの場合は、成功率は60%にもなります!この記事の主旨は、サプライズオンサイドキックをもっと頻繁に行うのが賢明な戦略だということです。私も同感です。セインツの見事な動きでした。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
シーズンが進み、天候が悪化し、チームの最近のパフォーマンスに関する情報が増えるにつれて、フットボールのトータルベッティングにはどのような力学が影響するのでしょうか?ラインのエラーを見つけるのはどれくらい簡単(または難しい)でしょうか?
この質問に答えるために、私は 1983 年から 2009 年までの各シーズンに基づいて、NFL の週番号別に獲得した平均ポイントをグラフ化しました。次のグラフは結果を示しています。
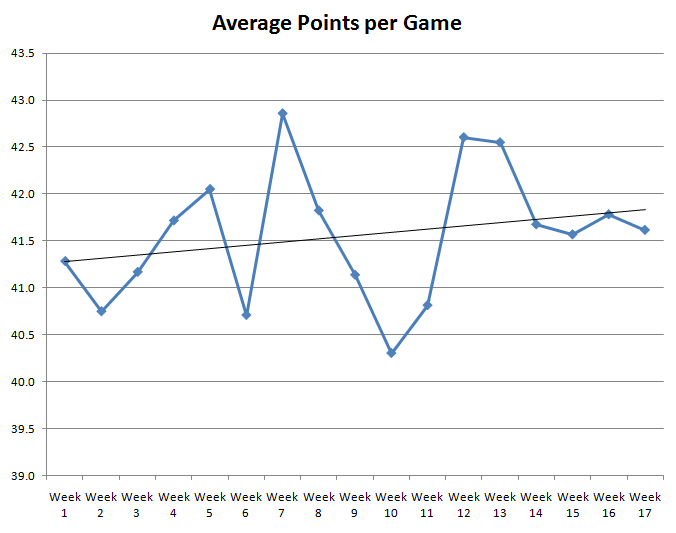
ご覧の通り、線は大きく上下しています。細い黒線は最小二乗法による最適近似線で、全体的に上昇傾向を示しています。季節が進み気温が下がると、平均得点はわずかに上昇しますが、これはランダムな変動である可能性も十分にあります。
私の理解できる範囲はこれくらいです。天候がスポーツベッティング全般にどのような影響を与えるかについて、一般的な意見を伺うため、この分野の専門家である友人のジェイソン・ビーンに話を聞きました。彼の意見は次のとおりです。
ほとんどの場合、試合に最も影響を与える天候の要素は風ですが、風だけが要因ではありません。野球やその他の屋外スポーツでは、特にシーズン序盤および終盤の午後の野球の試合では、影も同様に影響を与えることがあります。雨や雪は、フットボールでは多くの人が考えるほど大きな要因ではありません。一般的に、攻撃と守備の両方に等しく影響を与えるからです。一例として、ディフェンスバックとワイドレシーバーが挙げられます。雨と雪はどちらも同様にスピードを低下させるため、どちらの側にも優位性を与えません。フットボールでは、風によってパスゲームとキックゲームが簡単に消滅することがあります。パスチームが強い横風のためにほぼすべてのプレーでランを強いられた試合を見たことがあります。めったに起こりませんが、風が試合の最終的な勝敗を分けることもあります。この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
NFL では、平均して、得点後に他のチームが次に得点する確率はどれくらいですか?
2000~2009 年の NFL シーズンに基づくと、答えは 57% です。
NFLチームが前回の試合で大敗した場合、次の試合でそのチームに賭ける方が良いでしょうか、それとも賭けない方が良いでしょうか?大勝したチームでも同じことが言えます。大敗したチームは「何か証明したいことがある」と感じ、大勝したチームは自信過剰で怠惰になっているとよく聞きますが、本当でしょうか?
21点以上の差で負けた場合、チームは51.66%の確率でスプレッドをカバーすると示しました。しかし、これは誤差の範囲内です。次の表は、前回の試合における同じチームの勝敗に基づいて、前回の試合のスプレッドに対する結果を示しています。結果は50%から大きく外れることはなく、常に標準偏差の範囲内です。基本的に、スプレッドに対する勝敗と、前回の試合までのチームの勝ち点数または負け点数の間には統計的な相関関係は見られません。
前回の試合の勝利または敗北の差に応じてスプレッドに対して勝利、敗北、または引き分け
| 前回の試合結果 | スプレッドに勝つ | スプレッドに対する損失 | タイ・アゲインスト・スプレッド | 勝率 | 標準偏差 |
| 21点以上で勝つ | 233 | 247 | 17 | 48.54% | 2.28% |
| 14対20で勝利 | 235 | 219 | 11 | 51.76% | 2.35% |
| 10対13で勝利 | 188 | 180 | 8 | 51.09% | 2.61% |
| 7対9で勝利 | 198 | 181 | 12 | 52.24% | 2.57% |
| 4対6で勝利 | 164 | 170 | 12 | 49.10% | 2.74% |
| 3点差で勝利 | 202 | 212 | 14 | 48.79% | 2.46% |
| 2点差で負けて2点差で勝つ | 184 | 188 | 14 | 49.46% | 2.59% |
| 3点差で負け | 209 | 207 | 12 | 50.24% | 2.45% |
| 4対6で敗北 | 174 | 163 | 9 | 51.63% | 2.72% |
| 7対9で敗北 | 187 | 195 | 9 | 48.95% | 2.56% |
| 10対13で敗北 | 173 | 189 | 14 | 47.79% | 2.63% |
| 14対20で敗北 | 220 | 232 | 15 | 48.67% | 2.35% |
| 21点以上の負け | 249 | 233 | 15 | 51.66% | 2.28% |
2000 年シーズンの第 1 週から 2010 年シーズンの第 4 週までのすべての NFL ゲームに基づいた表。
Pinnacleスポーツブックがオッズを小数点形式で掲載するようになりました。スポーツブックのオッズを小数点形式からアメリカ式に変換するにはどうすればいいですか?
2010年10月25日のマンデーナイトフットボールの試合を例に考えてみましょう。ヨーロッパのオッズは次のように掲載されています。
ニューヨーク・ジャイアンツ 2.750
ダラス・カウボーイズ 1.513
どちらの数字も、賭けた1ユニットに対して、勝った場合に戻ってくる金額を表しています。これには元の賭け金も含まれます。小数オッズが2以上の場合、変換は簡単です。1を引いてから100を掛けます。オッズが2未満の場合は、(1) 1を引いて、(2) 逆数を取り、(3) -100を掛けます。
計算式を好む方のために、小数オッズが x を支払う場合、同等のアメリカン オッズの計算は次のとおりです。
x>=2の場合: 100*(x-1)
x<2の場合: -100/(x-1)
上記の例では、アメリカ形式の行は次のようになります。
ニューヨーク・ジャイアンツ:100*(2.750-1) = +175
ダラス・カウボーイズ: -100/(1.513-1) = -195
Pinnacle の Web サイトの左上、ロゴの上にあるプルダウン メニューで「American Odds」を選択すると、すべてのラインを自動的に変換することもできます。
以前ブックメーカーをやっていた友人と、今シーズンのNFLレギュラーシーズン全試合の50%以上の試合でスプレッドを上回れるという賭けをしました。私が勝てば1000ドル、彼が勝てば500ドルを支払います。2010年10月31日(日)までに19試合のリードがあり、彼は取引を持ちかけています。ここで、どんなオファーを受けるのが良いでしょうか?
素晴らしい賭けだ。まるで赤ちゃんからキャンディーを奪うみたいだ。コイン投げで2対1の配当を得るようなものだ。引き分けなら勝ちだから、なおさら良い。
本稿執筆時点で、レギュラーシーズンは256試合中95試合が終了しています。二項分布を用いると、あなたの勝利確率は99.87%となります。妥当な決済価格は998.02ドルです。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
ラスベガスのスポーツブックが、大学フットボールの合計オッズが明らかに間違っていました。マーケットのオッズは43でしたが、ブックメーカーは53で提示していました。そこで、注目を集めたり、オッズが変動したりしないように、少額ずつアンダーに20回ほど賭けました。予想通り、勝ちました。賭け金を支払いに出すのが不安です。カジノ側が支払いを拒否するのは正当なのでしょうか?
10対1で賭けてもいいと思いますが、事前に少し説明があるかもしれません。私が少し疑問に思うのは、スポーツブックはゲーミング・コントロール・ボード(GAB)の許可を得て、明らかに誤って行われた賭けを取り消すことができるからです。
「ブックメーカーは、会長の事前の書面による承認なしに、一方的に賭けを取り消すことはできない。」――ネバダ州規則22.115
この権利は存在しますが、逸話的な証拠に基づくと、実際に行使されることはほとんどありません。どうなるか教えてください。
追伸:質問者から、特に問題なく支払われたと後で知らされました。
スーパーボウルで、最初にタッチダウンを決めた選手の名字のスクラブルポイント数を賭ける賭けがあります。オッズはオーバーとアンダーの両方で10.5倍、-115倍です。どちらが良い賭けでしょうか?
このような独創的な賭け方が好きです。ボイドカジノだけでなく、パームス、エル・コルテス、サウスポイントなどでも見かけます。この疑問に答えるために、特定の選手が最初のタッチダウンを決めるという賭け方をいくつか見てみました。そのオッズは下の表の2列目に示されています。分かりやすくするために、フィールドゴールが5対1、タッチダウンが1回も決まらないオッズは100対1で考慮していません。次に、これらの勝利を3列目の「公正な確率」に変換しました。これは、賭けが完全に公正であるために必要な勝利の確率です。これらの確率は、各勝利の配当を低く抑えているために高く設定されており、合計は166%となっています。4列目の「調整された確率」は、公正なオッズを1.660842で割った値で、合計確率は100%です。5列目は、各プレイヤーの名前のスクラブルポイント数を示しています。6列目の「期待スクラブルポイント」は、確率とスクラブルポイントの積です。右下のセルは、平均スクラブルポイントが14.18521であることを示しています。
平均的に見ると、オーバーが正解のようです。プレイヤーごとにスクラブルの得点を11点以上取る確率は0.641894で、これは-179というフェアラインに換算されます。つまり、-115のオーバーは素晴らしい賭けと言えるでしょう。115を賭けると、プレイヤーはオーバーに対して20%のアドバンテージを得ます。
残念ながら、私が賭けようとした時には、ラインは -180 に移動していました。
スクラブル、スーパーボウルで初のタッチダウンを決めた選手にポイント
| 名前 | 掲載オッズ | 公平な確率 | 調整確率 | スクラブルポイント合計 | 予想スクラブルポイント |
|---|---|---|---|---|---|
| メンデンホール | 4 | 0.200000 | 0.120421 | 20 | 2.408416 |
| ジェニングス | 4.5 | 0.181818 | 0.109473 | 22 | 2.408416 |
| スタークス | 5 | 0.166667 | 0.100351 | 10 | 1.003507 |
| ウォレス | 7 | 0.125000 | 0.075263 | 15 | 1.128945 |
| 区 | 8 | 0.111111 | 0.066900 | 8 | 0.535204 |
| ロジャース | 8 | 0.111111 | 0.066900 | 10 | 0.669005 |
| ネルソン | 8 | 0.111111 | 0.066900 | 9 | 0.602104 |
| ミラー | 10 | 0.090909 | 0.054737 | 11 | 0.602104 |
| ドライバ | 10 | 0.090909 | 0.054737 | 11 | 0.602104 |
| ジョーンズ | 12 | 0.076923 | 0.046316 | 15 | 0.694735 |
| ロスリスバーガー | 12 | 0.076923 | 0.046316 | 22 | 1.018945 |
| サンダース | 15 | 0.062500 | 0.037632 | 9 | 0.338684 |
| 茶色 | 18 | 0.052632 | 0.031690 | 12 | 0.380276 |
| レッドマン | 18 | 0.052632 | 0.031690 | 11 | 0.348587 |
| クォーレス | 20 | 0.047619 | 0.028672 | 19 | 0.544761 |
| クーン | 25 | 0.038462 | 0.023158 | 12 | 0.277894 |
| ジャクソン | 30 | 0.032258 | 0.019423 | 24 | 0.466145 |
| ムーア | 30 | 0.032258 | 0.019423 | 8 | 0.155382 |
| 合計 | 1.660842 | 1.000000 | 14.185214 | ||
残念ながら、私が賭けるためにカジノに戻ったときには、ラインは -180 に移動していました。
追伸:試合の数時間前に-170で賭けました。残念ながら負けました。最初にタッチダウンを決めた選手はジョーディ・ネルソンでした。ネルソンはスクラブルで9ポイント持っています。
2010-2011 シーズンの NFL で、アンダードッグはスプレッドに対してどのような成績を残しましたか?
267試合のうち、フェイバリットがスプレッドに勝利したのは128回、アンダードッグが勝利したのは133回、プッシュが6試合ありました。成立したベットのうち、アンダードッグの勝率は51.0%でした。
さらに興味深いのは、オーバーとアンダーの勝率です。オーバーは148勝、アンダーは114勝、そして5勝がプッシュとなりました。成立した賭けのうち、オーバーの勝率は56.5%でした。成立した262試合のうち、アンダーが114勝以下で勝つ確率は2.1%です。
2011年11月6日のラムズ対カーディナルスの試合で、ラムズは第3クォーターで2つのセーフティを獲得しました。その確率はどれくらいでしょうか?
過去の経験に基づくと、1 試合あたり少なくとも 1 回のセーフティの確率は 5.77% です。
1試合あたりのセーフティの予想数は -ln(1-0.0577) = 0.0594 となります。
チームあたりの四半期あたりの予想数は 0.0594/8 = 0.0074 になります。
1クォーター中に同じチームが2回セーフティを獲得する確率は、e -0.0074 ×0.0074 2 /fact(2) = 36,505分の1となる。
NFLのシーズンは267試合あり、267×8=2,136チームのクォーター戦があります。つまり、私の推定では、これは平均して36,505÷2,136=17.1年に1回発生することになります。
これはあくまでも大まかな推測として捉えてください。簡潔にするため、ゲームには考慮していない要素がいくつかあります。
ニュージャージー州ポップコーンパーク動物園のラクダ「プリンセス」の話をご存知ですか?NFLのハンディキャップスプレッドで88勝51敗という記録を樹立しています。そのオッズはどれくらいでしょうか?
プッシュを除けば、139回のピックのうち88勝以上を挙げる確率は0.00107355、つまり931分の1です。これはかなり期待外れです。きっと、誰も記事にしていない、もっと悪い成績を収めた動物が930匹もいるでしょう。プリンセスについてもっと知りたい方は、ESPN.comの記事「ニュージャージーのラクダがジャイアンツがペイトリオッツに勝つと予想」をご覧ください。
- ビルズ +3.5 (+3)
- チャージャーズ +7.5 (+7)
- カージナルス -2.5 (-3)
- ドルフィンズ -2.5 (-3)
- ベアーズ +2.5 (0)
この賭けにおける私の有利性は何ですか?
私はオッズが 25 対 1 であると仮定します。これは、ゴールデン ナゲット、サウス ポイント、ウィリアム ヒルのスポーツ ブック ファミリーのハーフ ポイント カードで利用可能です。
下の表は、取得したラインと市場価格ラインを示しています。
まず、アンダードッグがスプレッドを上回る確率は51.6%です。これは、アンダードッグのフェアラインが-106.6に相当します。つまり、アンダードッグでは6.6ベーシスポイントの利益を得ているのに対し、フェイバリットではその利益を失うことになります。
次に、 NFLでハーフポイントを購入する際の私の表は、ハーフポイントごとに支払うべき適正価格を示しています。例えば、3ポイントでハーフポイントを獲得するには、-121.4、つまり21.4ベーシスポイントを支払う価値があります。
表は、あなたが何ベーシスポイントを得るかの内訳を示しています。ベアーズの場合、1と2のベーシスポイントを2倍にしました。これらの数値を超えると損失が利益に変わるからです。
この表は、合計ベーシスポイントを当選確率に変換します。式はp = (100+b)/(200+b)です。ここで、pは当選確率、bはベーシスポイント数です。
一番下の行は、各レグの勝敗数を掛け合わせたもので、パーレーの勝率は0.046751です。オッズが25対1の場合、この賭けの期待リターンは0.046751×25-1=0.168783となります。つまり、16.9%のアドバンテージです。おめでとうございます!
ルードボイ・パーレイカード
| チーム | パーレイ カード | 公平 | アンダードッグ 基礎 ポイント | 合計 余分な ポイント | 合計 | 確率 |
|---|---|---|---|---|---|---|
| 請求書 | 3.5 | 3 | 6.6 | 20.8 | 27.4 | 0.560246 |
| チャージャーズ | 7.5 | 7 | 6.6 | 11.9 | 18.5 | 0.542334 |
| カージナルス | -2.5 | -3 | -6.6 | 20.8 | 14.2 | 0.533147 |
| イルカ | -2.5 | -3 | -6.6 | 20.8 | 14.2 | 0.533147 |
| クマ | 2.5 | 0 | 0 | 18.0 | 18.0 | 0.541321 |
| 製品 | 0.046751 | |||||
シアトルの自動車販売店が、シーホークスがジャイアンツを完封したせいで42万ドルを支払わなければならなかったという話を聞きましたか? 保険に7,000ドル支払わなければならなかったと読んだのですが、妥当な保険料はいくらだったのでしょうか?
1983年から2012年までのNFLの全試合を振り返ると、どの試合でも特定のチームがシャットアウトされています。しかし、7点差のアンダードッグとして、平均的なオーバー/アンダーの試合でジャイアンツがシャットアウトされる確率は平均よりも高かったと私は考えます。この試合のオーバー/アンダーは41でした。少し代数を使って、ジャイアンツの予想得点数を計算してみましょう。
させて:
s=シーホークスの得点
g=ジャイアンツポイント
ポイントスプレッドとオーバー/アンダー合計に基づくと、s+g=41、s=g+7 であることがわかります。
2 番目の方程式を 1 番目の方程式に代入します。
(g+7)+g = 41
2g + 7 = 41
2g = 34
グラム = 17
次に、1983年から2012年のシーズンに基づいて、各チームの推定得点数から完封確率を見てみましょう。サンプル数が0の行は省略しました。
完封確率
| 推定 ポイント | サンプルサイズ | 完封 | 比率 |
|---|---|---|---|
| 5.25 | 1 | 0 | 0.0% |
| 6.50 | 1 | 0 | 0.0% |
| 7.75 | 1 | 0 | 0.0% |
| 8.00 | 1 | 0 | 0.0% |
| 8.25 | 3 | 0 | 0.0% |
| 8.50 | 2 | 0 | 0.0% |
| 8.75 | 2 | 0 | 0.0% |
| 9.00 | 2 | 0 | 0.0% |
| 9.50 | 4 | 0 | 0.0% |
| 9.75 | 6 | 1 | 16.7% |
| 10.00 | 10 | 1 | 10.0% |
| 10.25 | 7 | 0 | 0.0% |
| 10.50 | 14 | 2 | 14.3% |
| 10.75 | 7 | 1 | 14.3% |
| 11時00分 | 13 | 1 | 7.7% |
| 11.25 | 21 | 1 | 4.8% |
| 11.50 | 22 | 3 | 13.6% |
| 11.75 | 23 | 1 | 4.3% |
| 12時 | 34 | 2 | 5.9% |
| 12.25 | 36 | 7 | 19.4% |
| 12.50 | 41 | 3 | 7.3% |
| 12.75 | 39 | 4 | 10.3% |
| 13.00 | 55 | 1 | 1.8% |
| 13.25 | 58 | 5 | 8.6% |
| 13.50 | 78 | 1 | 1.3% |
| 13.75 | 89 | 5 | 5.6% |
| 14.00 | 92 | 4 | 4.3% |
| 14.25 | 108 | 7 | 6.5% |
| 14.50 | 117 | 8 | 6.8% |
| 14.75 | 141 | 7 | 5.0% |
| 15.00 | 160 | 7 | 4.4% |
| 15.25 | 160 | 7 | 4.4% |
| 15.50 | 213 | 7 | 3.3% |
| 15.75 | 198 | 11 | 5.6% |
| 16時 | 206 | 6 | 2.9% |
| 16.25 | 221 | 12 | 5.4% |
| 16.50 | 241 | 10 | 4.1% |
| 16.75 | 273 | 7 | 2.6% |
| 17.00 | 306 | 8 | 2.6% |
| 17.25 | 305 | 8 | 2.6% |
| 17.50 | 306 | 10 | 3.3% |
| 17.75 | 323 | 4 | 1.2% |
| 18時 | 299 | 8 | 2.7% |
| 18.25 | 332 | 8 | 2.4% |
| 18.50 | 309 | 9 | 2.9% |
| 18.75 | 307 | 7 | 2.3% |
| 19.00 | 356 | 8 | 2.2% |
| 19.25 | 389 | 5 | 1.3% |
| 19.50 | 361 | 5 | 1.4% |
| 19.75 | 343 | 6 | 1.7% |
| 20.00 | 402 | 8 | 2.0% |
| 20.25 | 379 | 6 | 1.6% |
| 20.50 | 359 | 3 | 0.8% |
| 20.75 | 353 | 5 | 1.4% |
| 21時 | 344 | 1 | 0.3% |
| 21.25 | 317 | 3 | 0.9% |
| 21.50 | 341 | 2 | 0.6% |
| 21.75 | 331 | 1 | 0.3% |
| 22.00 | 369 | 1 | 0.3% |
| 22.25 | 336 | 0 | 0.0% |
| 22.50 | 316 | 2 | 0.6% |
| 22.75 | 280 | 3 | 1.1% |
| 23.00 | 311 | 1 | 0.3% |
| 23.25 | 290 | 3 | 1.0% |
| 23.50 | 279 | 1 | 0.4% |
| 23.75 | 255 | 1 | 0.4% |
| 24.00 | 246 | 1 | 0.4% |
| 24.25 | 219 | 0 | 0.0% |
| 24.50 | 230 | 2 | 0.9% |
| 24.75 | 230 | 1 | 0.4% |
| 25.00 | 212 | 2 | 0.9% |
| 25.25 | 207 | 0 | 0.0% |
| 25.50 | 176 | 1 | 0.6% |
| 25.75 | 154 | 0 | 0.0% |
| 26.00 | 154 | 1 | 0.6% |
| 26.25 | 113 | 0 | 0.0% |
| 26.50 | 137 | 0 | 0.0% |
| 26.75 | 122 | 0 | 0.0% |
| 27.00 | 95 | 0 | 0.0% |
| 27.25 | 98 | 0 | 0.0% |
| 27.50 | 83 | 0 | 0.0% |
| 27.75 | 81 | 0 | 0.0% |
| 28.00 | 82 | 0 | 0.0% |
| 28.25 | 55 | 1 | 1.8% |
| 28.50 | 56 | 0 | 0.0% |
| 28.75 | 51 | 0 | 0.0% |
| 29.00 | 48 | 0 | 0.0% |
| 29.25 | 34 | 0 | 0.0% |
| 29.50 | 24 | 0 | 0.0% |
| 29.75 | 25 | 0 | 0.0% |
| 30.00 | 24 | 0 | 0.0% |
| 30.25 | 21 | 0 | 0.0% |
| 30.50 | 18 | 0 | 0.0% |
| 30.75 | 23 | 0 | 0.0% |
| 31.00 | 16 | 0 | 0.0% |
| 31.25 | 15 | 0 | 0.0% |
| 31.50 | 8 | 0 | 0.0% |
| 31.75 | 3 | 0 | 0.0% |
| 32.00 | 6 | 0 | 0.0% |
| 32.25 | 7 | 0 | 0.0% |
| 32.50 | 6 | 0 | 0.0% |
| 32.75 | 3 | 0 | 0.0% |
| 33.00 | 4 | 0 | 0.0% |
| 33.25 | 6 | 0 | 0.0% |
| 33.50 | 5 | 0 | 0.0% |
| 34.75 | 4 | 0 | 0.0% |
| 35.00 | 2 | 0 | 0.0% |
| 35.50 | 1 | 0 | 0.0% |
| 36.00 | 2 | 0 | 0.0% |
| 36.25 | 1 | 0 | 0.0% |
| 36.50 | 1 | 0 | 0.0% |
| 37.25 | 1 | 0 | 0.0% |
| 37.75 | 2 | 0 | 0.0% |
| 42.25 | 1 | 0 | 0.0% |
次のステップはここで説明するには複雑すぎるが、推定ポイント数に基づいて完封の確率を計算する式を開発しました。
p = 推定ポイント。
x = 1.562545 -0.302485 * p
完封確率 = e x /(1+e x )
次のグラフは、14 ~ 22 ポイントでの完封の実際および推定確率を示しています。
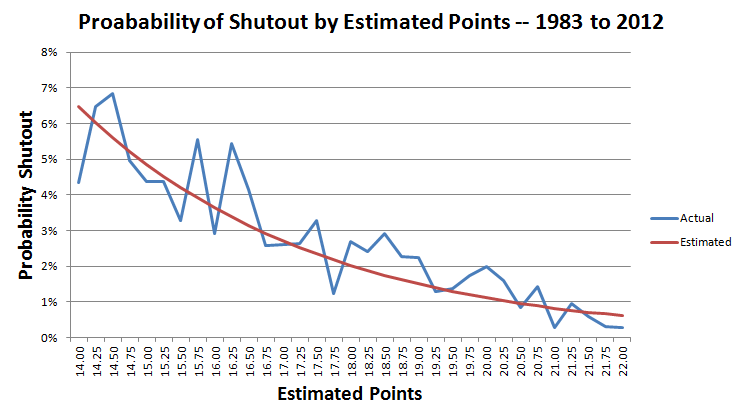
問題の試合ではジャイアンツは17点を獲得すると予想していた。
表の上の式を使用します。
x = 1.562545 -0.302485 * 17 = -3.579706
完封確率 = exp(-3.579706)/( exp(-3.579706)+1) = 2.71%。正確には0.0271275。
ジャイアンツが完封負けした場合、ディーラーは42万ドルを支払わなければならなかったことを考えると、保険料は42万ドル × 0.0271275 = 11,394ドルとなるはずです。通常、このような異例のプロモーションを実施する保険会社は、保険料を2倍に引き上げるので、保険料は22,788ドルになるはずでした。つまり、ディーラーが支払った7,000ドルという保険料は、まさに破格の値段だったのです。仮に社長が計算を見直したとしても、7,000ドルという保険料を計算した人の立場にはなりたくないですね。
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されました。
ラスベガスで最高の先物オッズを提供しているのは誰ですか?
2015 年のスーパーボウルの先物賭けによると、ラスベガスのさまざまなスポーツブック グループの平均ハウス エッジは次のとおりです。
スポーツ先物取引におけるハウスエッジ
| スポーツブック | ハウスエッジ |
|---|---|
| CGテクノロジー | 21.90% |
| ウィリアムヒル | 26.63% |
| ウィン | 27.96% |
| シーザーズ | 35.49% |
| 駅/エル・コルテス | 38.33% |
| ゴールデンナゲット | 39.75% |
| MGM | 40.88% |
| ボイド/コースト | 49.35% |
| TI | 57.93% |
あらゆる先物ベットの平均ハウスエッジを計算するには、私のスポーツ先物計算機を使用してください。
ジェリーズ・ナゲットがNFLティーザーの魅力的なオッズを提供しなくなったと聞きました。本当ですか?
残念ながら、そうなのです。ジェリーズ・ナゲットは、2レグ6ポイントのNFLティーザーで-110、3レグで+180、4レグで+300という寛大なオッズを提供していた最後の店でした。ウォン・ティーザー(3ポイントと7ポイントの勝利点差を越える)を利用することで、これは確実に有利な賭けとなりました。
ラスベガスの現在のパーレーとティーザーのオッズはすべて、Wizard of Vegas.com の私のスポーツブック調査でご覧いただけます。
フットボールのティーザー全般の詳細については、私のNFL のティーザーベットのページをご覧ください。
NFL では、あるスポーツブックでは 50 以上に賭け、別のスポーツブックでは 52.5 以下に賭けるのは良い賭けですか?
このような質問には、 NFLにおける私の代替トータルベットが使えます。これにより、トータルベットで追加ポイントを獲得する確率と公平なラインが分かります。
適正なオーバー/アンダーラインが51だと仮定しましょう。最初の表は、52.5以下の賭けで勝つ確率が、引き分けがないと仮定した場合54.4%であることを示しています。3番目の表は、オーバーの賭けで勝つ確率が53.5%であることを示しています。
10%のジュースに勝つには、11/21 = 52.38%の勝率が必要です。この2つの賭けの平均は53.95%なので、真ん中の賭けを選びましょう。あなたのアドバンテージは3.0%です。
NFLレギュラーシーズン終了直後、この質問を書いている時点で、Bovadaはカロライナ・パンサーズのNFC優勝オッズを18対1としています。彼らはアリゾナとの初戦で既に6ポイントの優位に立っています。あと2ポイント差です。
カロライナがNFCで優勝することに賭けて、その途中でヘッジして、カロライナが誰と対戦するかにマネーラインを賭けて、勝利を確実にできると思いませんか?
いいえ!先物取引とマネーラインでのフェイバリットへの賭けは、サッカーの賭けにおいて最悪の賭け方です。これは、マイナスの賭けを積み重ねて合計がプラスになることを期待する、まるでベッティングシステムのように聞こえます。しかし、おそらく納得してもらうにはそれ以上の情報が必要でしょうから、数字を見てみましょう。
まず第一に、パンサーズがプレーオフに出場できたのは、NFC南地区というひどい地区の中で、最も悪くないチームだからだ。彼らの成績は7勝8敗で、シーズンを通しての得点よりも35点多く失点している。
そんなにひどいなら、なぜアリゾナ・カーディナルズに対して6ポイントの優位性があるのだろう?と疑問に思う人もいるかもしれない。アリゾナがプレーオフに進出できたのは、最初の6試合でカーソン・パーマーの活躍が大きかった。彼は6試合目で負傷したが、それでも辛うじてプレーオフ進出を果たした。しかも、カロライナはホームフィールドアドバンテージを享受している。
カロライナがアリゾナに対して 6 ポイント有利であることを考えると、カロライナがその試合に勝つ確率は 70.3% であると示します。
仮に勝ったとしても、NFC優勝にはグリーンベイとシアトルの両方に勝たなければならない可能性が高いでしょう。この2チームに勝つ確率はどれくらいでしょうか? プレーオフのルール上、両試合ともビジターチームとなることを覚えておいてください。
どの試合でも、ポイントスプレッドの大まかな概算を簡単に得る方法があります。ホームチームのポイントスプレッドを計算するウィザード式は以下の通りです。
(アウェイチームの1試合あたりの純得点) - (ホームチームの1試合あたりの純得点) - 2.67。
アリゾナとグリーンベイの仮想対戦を見てみましょう。
2014年シーズン、カロライナはシーズンを通してネットポイントが-35です。グリーンベイは+138です。シーズン中に16試合が行われるため、両方の数字を16で割ると、1試合あたりの平均勝利差は次のようになります。
カロライナ: -2.1875
グリーンベイ:+8.6250
私の計算式を使用すると、ホームチームのグリーンベイのスプレッドは -2.1875 - 8.6250 - 2.67 = -13.4825 になるはずです。
つまり、グリーンベイはカロライナに対して約13.5ポイントの優位性を持つことになります。このステップでは計算は省略しますが、カロライナが13.5ポイントの劣勢で勝利する確率は14.3%です。
シアトルはグリーンベイとほぼ同等の好成績を収めており、シーズン通算ネットポイントは140ポイントです。そのため、カロライナがこの試合に勝利する確率も約14.3%となります。
カロライナが3試合すべて勝利するオッズは、70.3% × 14.3% × 14.3% = 1.44%です。つまり、この確率での公平な先物賭けは68.6対1です!
確かに、デトロイトかダラスが運が良ければカンファレンス・チャンピオンシップに進出する可能性があると主張することもできます。また、カロライナがグリーンベイとシアトルに勝つオッズには正の相関関係があると主張することもできます。しかし、私の大まかなフェアラインが68.6倍で、あなたが得るのはわずか18倍であるという事実に比べれば、それらは取るに足らない考慮事項です。
マネーラインでフェイバリットに賭ける際のコストも考慮する必要があります。これは一般的に最悪の賭け方です。堅実なベッターはマネーラインで大フェイバリットに賭けるのが好きで、逆方向にバリューを生み出します。マネーラインで7ポイント以上のアンダードッグに賭けるのは、ほぼ公平な賭けと言えるでしょう。つまり、フェイバリットに賭けるベッターがすべての利益を負担することになります。
少し寛大に、アリゾナに+250のオッズを付け、続く2試合で5対1のレイズを取れると仮定しましょう。また、カロライナに18対1のオッズで100ドル賭けたとしましょう。
まず、ヘッジとしてアリゾナに+250の40ドルを賭けます。アリゾナが勝てば、その賭けで100ドルの利益、先物で100ドルの損失で、損益はゼロになります。
カロライナがアリゾナに勝った場合、シアトルに700ドル賭けて140ドルの利益を得られます。シアトルが勝てば(当然勝つはずです)、140ドルの利益が出ます。これでアリゾナと先物で失った損失を取り戻せるので、元本はゼロになります。
カロライナが番狂わせを起こした場合、アリゾナ、シアトル、そして先物に賭けて失った840ドルを取り戻すには、4,200ドルを賭けなければなりません。カロライナが負ければ、損失はゼロになります。勝てば、40ドル+700ドル+4,200ドル=4,940ドルの損失になります。先物で勝った1,800ドルでは、その損失を取り戻すには十分ではありません。
最後に、カロライナが NFC で優勝し、その途中でリスクを負うという考えは、非常に無謀です。
自殺プールについてのアドバイスは何ですか?
ご存知ない方のために説明すると、自殺プールとは、最後の1人になるまで生き残るためのコンテストです。一般的にはNFLをモデルにしていますが、どのスポーツリーグでも構いません。基本的なルールは以下のとおりです。
- すべてのプレイヤーはプレイするために同じ金額を支払います。
- 毎週、各プレイヤーはその週の1試合の勝者を予想する必要があります。すべての試合はスプレッドではなく、ストレートアップで採点されます。
- プレイヤーが間違った場合は、直ちにコンテストから排除されます。
- プレイヤーは同じチームを複数回選択することはできません。
- 最後に残った人が賞金を獲得します。
プールを運営している人が分け前を得る、参加者が数人に減ったら相互の合意がある場合に限りポットを分割する、などの追加ルールがある場合があります。
先に進む前に、 officefootballpool.comの昨シーズンの結果を紹介します。
オフィスフットボールプール — 2014年シーズン
| 週 | チーム | 広める | おすすめ |
|---|---|---|---|
| 1 | フィル | -10.5 | 54 |
| 1 | シック | -7 | 29 |
| 1 | ピット | -6.5 | 14 |
| 1 | デット | -6 | 6 |
| 1 | ケンブリッジ | -3 | 5 |
| 1 | NYJ | -5.5 | 5 |
| 1 | 北東 | -4 | 1 |
| 1 | SF | -4.5 | 1 |
| 1 | セントルイス | -3.5 | 1 |
| 2 | デン | -12.5 | 38 |
| 2 | イギリス | -8 | 23 |
| 2 | いいえ | -6.5 | 7 |
| 2 | SF | -7 | 5 |
| 2 | 結核 | -5.5 | 3 |
| 2 | 洗う | -6 | 2 |
| 2 | シン | -5.5 | 1 |
| 2 | 北東 | -5.5 | 1 |
| 3 | 北東 | -14 | 44 |
| 3 | いいえ | -10 | 16 |
| 3 | アトル | -6.5 | 3 |
| 3 | シン | -6.5 | 1 |
| 3 | 工業 | -6 | 1 |
| 4 | SD | -13 | 34 |
| 4 | 工業 | -7.5 | 20 |
| 4 | ピット | -7.5 | 10 |
| 4 | バル | -3 | 1 |
| 5 | いいえ | -10 | 21 |
| 5 | イギリス | -8 | 13 |
| 5 | デン | -7.5 | 6 |
| 5 | デット | -6.5 | 5 |
| 5 | フィル | -6.5 | 3 |
| 5 | ダル | -6.5 | 2 |
| 5 | ピット | -6 | 2 |
| 5 | SD | -6.5 | 1 |
| 5 | 海 | -7 | 1 |
| 5 | SF | -5 | 1 |
| 6 | 海 | -8.5 | 21 |
| 6 | デン | -9.5 | 13 |
| 6 | SD | -7 | 7 |
| 6 | シン | -6.5 | 5 |
| 6 | 10 | -4 | 2 |
| 6 | アトル | -3 | 1 |
| 6 | SF | -3 | 1 |
| 7 | 北東 | -9.5 | 9 |
| 7 | 海 | -6.5 | 9 |
| 7 | イギリス | -6.5 | 3 |
| 7 | バル | -6.5 | 2 |
| 7 | ブフ | -5.5 | 2 |
| 7 | 洗う | -5 | 2 |
| 7 | ダル | -6.5 | 1 |
| 8 | ダル | -9.5 | 12 |
| 8 | ケンブリッジ | -7 | 5 |
| 8 | クレブ | -7 | 1 |
| 8 | ミア | -6 | 1 |
| 9 | SF | -10 | 3 |
| 9 | シン | -10。5 | 2 |
| 9 | 海 | -14.5 | 2 |
| 10 | バル | -9.5 | 2 |
| 10 | シン | -6 | 1 |
| 10 | 海 | -9 | 1 |
| 11 | イギリス | -5.5 | 1 |
| 11 | 私の | -6 | 1 |
| 11 | いいえ | -7 | 1 |
| 12 | 工業 | -14 | 2 |
| 13 | バル | -6.5 | 1 |
| 13 | デット | -7 | 1 |
| 14 | いいえ | -10 | 1 |
「ピック」列は、そのチームを選んだプレイヤーの数を示します。
注目すべきは、誰も一度もアンダードッグを選ばなかったことです。497回の選考で、平均得点差は9.3でした。
なぜ彼らが第 14 週にピックを記録したのかはわかりません。その時点ではプレーヤーが 1 人しか残っていなかったからです。
他のプレイヤーの行動に関するこの研究に基づいて、自殺プールにおける私の基本戦略をご紹介します。これらはあくまで一般的なガイドラインであり、毎週必ず従わなければならない厳格なルールではありません。
- 敵は他の選手たちだということを忘れないで。NFLをハンディキャップすることばかり考えず、競争相手に勝つことに集中しましょう。
- 一番人気の馬を選ばないでください。ほとんどの人がそうするでしょう。その一番人気の馬が負けて、出場馬が大幅に減ることを期待しましょう。一番人気の馬が負けた時は、被害者ではなく生き残りたいものです。
- 同じチームを2度選んではいけないというルールを忘れないでください。とはいえ、常に強いチームを選べるわけではありません。時には、強いチームに楽勝をさせるために、平均的なチームと弱いチームを対戦させるべきでしょう。
- ハンディキャップは気にしないでください。ポイントスプレッドを、特定のピックで勝つ可能性の指標として利用してください。
- ある週に2つの圧倒的な人気チームがある場合、私はどちらも避けるでしょう。勝利の可能性の高い試合を選びつつ、大衆の予想に左右されないようバランスを取ることが重要です。ごく一般的なルールとして、特に最強チームを無駄にしたくない場合は、スプレッドが3番目に高いチームを選ぶのが良いでしょう。
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されています。
タッチダウン後のポイントに関する新しいルールがハーフポイントパーレーカードにどのような影響を与えるかについて、あなたの意見をお聞かせください。
他の読者のために、私の秘策の一つは、ハーフポイント・パーレーカードの3と7のポイントスプレッドから得られるハーフポイントの恩恵を活用することです。これは、非常にボラティリティが高いものの、確実なアドバンテージプレイであることを証明しました。
新ルールでは、エクストラキックの位置が15ヤードラインまで後退します。これにより、キックの成功確率が低下し、2ポイントコンバージョンの試みが増えるはずです。2ポイントコンバージョンの試みが増えれば、成否に関わらず、3点差や7点差で決着がつく試合は少なくなるはずです。つまり、ハーフポイントパーレーカードでこれらの重要な数字から追加のハーフポイントを得る価値は低下するということです。心配すべきでしょうか? 見てみましょう。
まず、心配すべき点ですが、これは当然のことです。他のルール変更によってディフェンスの積極性が損なわれ、得点が増加する試合が増えています。次のグラフは、1994年から2014年までの各シーズンにおける1試合あたりの平均得点を示しています。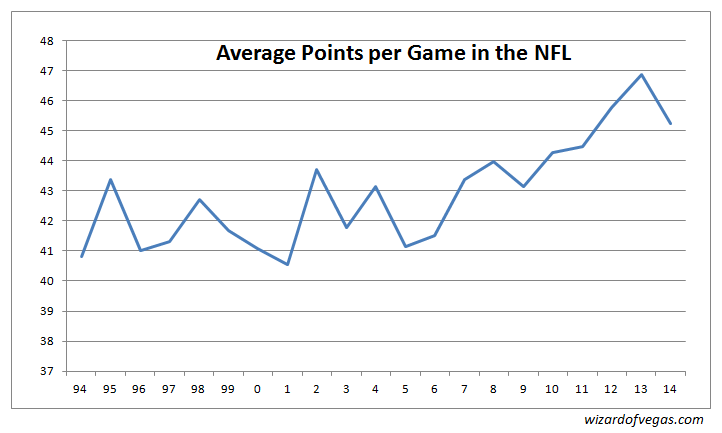
グラフが示すように、1試合あたりの平均得点は2006年までは42点前後で推移していました。しかし、2007年以降、平均得点は年間約0.5点ずつ上昇しています。このことから、平均得点の上昇が、特にマジックナンバーである3点と7点において、勝利点差の分布を平坦化させる傾向があるのではないかという疑問が生じます。次のグラフは、3点差と7点差の勝利点差の確率を年ごとに示しています。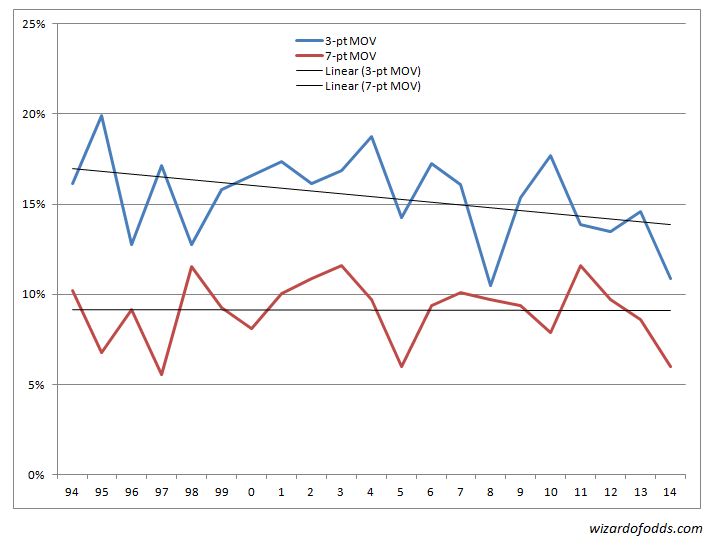
ご覧の通り、7点差で勝利する確率は9.1%で安定しています。一方、3点差で勝利する確率は着実に低下しており、特に2004年以降は顕著です。NFLでは3点差の試合が非常に多いため、これは好ましくない状況です。
3ポイント差での勝利が減った原因が何であれ、ハーフポイント・パーレーカードの価値は低下しています。新しいエクストラポイントルールによって、さらに悪化するのでしょうか?
私の答えは、影響は大きいものの、それほど大きくないということです。ルール変更前は、タッチダウンの約4.8%が2ポイントコンバージョンの試みに続いていました。この記事を書いている時点では、ルール変更後まだ2週間しか試合が行われていません。2015年シーズンの最初の2週間では、167回のタッチダウンのうち15回が2ポイントコンバージョンの試みに続いており、試み率は9.0%でした。
数学的に言えば、2ポイントコンバージョンを狙うのはもっと一般的になるべきだと私は思います。特に、分散を狙う弱いチームにとってはなおさらです。なぜそれがないのか理解できません。それはあなたの質問ではないのですが、どうしても言いたかったのです。
例えば、スプレッドに対して54%の勝率を安定して取れるとします。資金をできるだけ早く増やすには、3チームパーレーに6対1の配当でフラットベットする方が、より有利でしょうか?
いい質問ですね。11対10のレイドベットのアドバンテージは3.09%、パーレーベットのアドバンテージは10.22%です。パーレーベットの優位性は十分にありそうですね。
しかし、アドバンテージのあるプレイで資金を増やすための最適な戦略は、ケリー基準を用いることです。ケリーによれば、最適なベット額とは、ベット後の資金の期待対数値を最大化する額です。結果が2通りしかないベットの場合、最適なベット額は、アドバンテージを「1対1」で支払われる額で割った値となります。
ストレートベットの配当は10対11です。したがって、最適なベット額は0.030909/(10/11) = 0.034000となります。プレイヤーのアドバンテージが3.09%の場合、ストレートベットでは1ゲームあたりバンクロールの0.001051倍の勝利が期待できます。
パーレーの最適なベットサイズは0.102248/6 = 0.017041です。プレイヤーのアドバンテージが0.102248の場合、ストレートベットでは1ゲームあたりバンクロールの0.001742倍の勝利が期待できます。
しかし、ストレートベットの方が3回賭けられるので有利です。フラットベットの1ベットあたりの期待利益を3倍すると、3 × 0.001051 = 0.003153となります。これは、パーレーベットのバンクロール増加率よりも81%高い数値です。
資金が多すぎて最大賭け金の制限に達してしまった場合は、ラインを動かさない傾向のあるパーレーベットを最初に行い、その後ストレートベットを行うのがよいでしょう。
この質問は、 Wizard of Vegasの私のフォーラムで提起され、議論されています。
ご存知の通り、NFLではエクストラポイントは15ヤードラインからトライしなければなりませんが、2ポイントコンバージョンは2ヤードラインからトライする形に変更されました。この変更によって判定の計算は変わると思いますか?言い換えれば、今や正しいプレーとは何でしょうか?
これはギリギリの判定であり、NFLがルール変更の際に目指していたのはまさにこれだったと思います。判断を下す際に考慮すべき点は以下のとおりです。
- キックによる成功確率。
- 2ポイントコンバージョンを狙う場合の成功確率。
- 各チームが勝利する全体的な可能性。
試合終盤では、重要な数字を考慮することも非常に重要です。例えば、試合終盤でタッチダウンを決めて3点リードしている場合は、キックすべきです。キックが成功すれば4点リードとなり、相手チームはタッチダウンを取らなければ勝利できません。一方、2点を狙って失敗すれば、相手チームはフィールドゴールだけで同点に追いつくことができます。そのため、ここでは重要な数字が大きな要素とならない、試合序盤に限って考察することにします。
ご質問にお答えするために、シミュレーションプログラムを作成しました。かなり粗雑ではありますが、フィールドゴール、タッチダウン、ターンオーバーといったNFLの特性をかなり正確に反映できていると思います。
ケビン・ルディ氏による記事「エクストラポイントを15ヤードラインに移動するとどうなるか?」によると、15ヤードラインからエクストラポイントを獲得する確率は94.2%です。私は数値を概算するため、プログラムに94%を組み込んでいます。
2ポイントコンバージョンの成功率については、さらに意見が分かれています。これは、ディフェンスとオフェンスのパターンによって大きく異なることは明らかです。私は、2ポイントコンバージョンの成功率を46%から50%まで、1%ずつのグループに分けてシミュレーションを行いました。
各シミュレーションでは、一方のチームが常にキックし、相手チームが各成功確率でコンバージョンを狙うという設定にしました。また、両チームが常にキックするシミュレーションも実行し、2ポイントコンバージョンの結果を比較できるようにしました。
下の表1は、実力が同等の2チームの結果を示しています。チームAは常にタッチダウン後にキックを行います。表は、チームBがキックするか2ポイントコンバージョン(2PC)を狙うか、そしてその成功確率に応じて、チームBの勝利確率と1試合あたりの平均追加得点を示しています。
表1 — 同等のチーム
| チームB 戦略 | チームB おそらく。 勝つ | 平均 追加 ポイント |
|---|---|---|
| キック | 50.00% | 0.0001 |
| 2PC -- 46% | 49.76% | 0.0491 |
| 2PC -- 47% | 49.90% | 0.0000 |
| 2PC -- 48% | 50.05% | 0.0492 |
| 2PC -- 49% | 50.19% | 0.0980 |
| 2PC -- 50% | 50.33% | 0.1461 |
成功確率が47%の場合、キックであれツーポイントであれ、期待される追加得点は0.94点です。しかし、ツーポイントを狙う場合の勝利確率は0.1%低くなります。これは、もしミスした場合、相手チームが2本のフィールドゴールで同点に追いつくチャンスがあるためだと考えられます。このキーナンバー効果は非常に小さいですが、他の条件が同じであれば、保守的なキックを優先する傾向があることに留意してください。つまり、2チームの実力が同等であれば、ツーポイントコンバージョンの成功確率は少なくとも49%である必要があります。
下の表2は、2つの格差のあるチームの結果を示しています。チームAの方が強いです。チームAは常にタッチダウン後にキックします。上の表1と同じ統計値を示しています。
表2 — チームAが強い
| チームB 戦略 | チームB おそらく。 勝つ | 平均 追加 ポイント |
|---|---|---|
| キック | 28.83% | -7.0039 |
| 2PC -- 46% | 29.01% | -7.0519 |
| 2PC -- 47% | 29.16% | -7.0039 |
| 2PC -- 48% | 29.30% | -6.9568 |
| 2PC -- 49% | 29.45% | -6.9083 |
| 2PC -- 50% | 29.60% | -6.8595 |
表2は、記載されているすべての成功確率において、弱いチームが2ポイントコンバージョンを狙うべきであることを示しています。期待される総得点数が少ない45%の場合でもそうです。なぜそうなるのか疑問に思うかもしれません。それは、どんな試合でも弱いチームは変化を求めるべきであり、強いチームは変化を嫌うからです。
下の表3は、2つの格差のあるチームの結果を示しています。チームBの方が強いです。チームAは常にタッチダウン後にキックします。上記の表1と表2と同じ統計を示しています。表3 — チームBが強い
| チームB 戦略 | チームB おそらく。 勝つ | 平均 追加 ポイント |
|---|---|---|
| キック | 71.17% | 7.0042 |
| 2PC -- 46% | 70.53% | 6.9349 |
| 2PC -- 47% | 70.67% | 7.0030 |
| 2PC -- 48% | 70.82% | 7.0725 |
| 2PC -- 49% | 70.97% | 7.1412 |
| 2PC -- 50% | 71.12% | 7.2109 |
表3では、チームBがキックで勝利する確率が71.17%であることに注目してください。期待得点数は成功確率49%または50%の方が高いにもかかわらず、表に示されているすべての成功確率においてこの確率はそれよりも低い値です。その理由は、弱いチームは変化を求めるべきであり、強いチームはそれを避けるべきだからです。2ポイントコンバージョンの試みは試合にボラティリティをもたらすため、他の条件が同じであれば、弱いチームは強いチームよりも2ポイントコンバージョンを試みる傾向が強くなります。
カロライナ・パンサーズがレギュラーシーズンで16勝0敗するオッズはどれくらいでしょうか?どちらの賭けも得になるでしょうか?
はい +425?
-550はないですか?
大きな怪我、回復、出場停止などがなければ、実際のスプレッドに非常に近い、特定の試合の得点スプレッドを推定する方法があります。特定のチームの予想得点の計算式は次のとおりです。
[(平均攻撃ポイント) + (相手チームの平均失点)]/2 + (ホームでプレイしている場合は 1.5、それ以外の場合は -1.5)。
ポイントスプレッドは、(ビジターチームの予想ポイント)-(ホームチームの予想ポイント)となります。
第13週のセインツ戦を例に考えてみましょう。パンサーズはビジターチームです。パンサーズは今シーズン、平均32.3得点を記録しています。一方、セインツは平均30.8失点しています。私の計算式を用いると、パンサーズは(32.3+30.8)/2 - 1.5 = 30.05得点を獲得すると予想されます。
次に、セインツについても同じことをしてみましょう。セインツは今シーズン、1試合平均23.7得点を挙げています。一方、パンサーズは1試合平均18.6失点しています。私の計算式では、セインツの得点は(23.7 + 18.6)/2 + 1.5 = 22.65点となります。
したがって、パンサーズは30.05 - 22.65 = 7.4ポイントで勝利すると予想されます。次に、私のプロップベット計算機を使って各試合の勝利確率を計算してみましょう。計算機は試合のオーバー/アンダーを尋ねますが、ストレートで勝つチームを決める上で重要なのはスプレッドだけです。合計には、今シーズンのNFL平均である46を入力してください。ポイントスプレッドが7.4の場合、ホームチームの勝利のフェアラインは+271です。つまり、パンサーズのフェアラインは-271です。つまり、勝利確率は271/371 = 73.05%となります。
残りの4つのゲームについても同様に計算し、積を求めます。または、下の表を使用することもできます。
パンサーズ 第13週~第17週
| 週 | 反対 チーム | 位置 | 期待される パンサー ポイント | 期待される 対戦相手 ポイント | パンサーズ 勝利 マージン | パンサーズ 公平 ライン | 確率 勝つ |
|---|---|---|---|---|---|---|---|
| 13 | 聖人 | 離れて | 30.05 | 22.65 | 7.4 | -271 | 0.730458 |
| 14 | ファルコンズ | 家 | 28.3 | 19.6 | 8.7 | -323 | 0.763593 |
| 15 | ジャイアンツ | 離れて | 27.05 | 23.85 | 3.2 | -154 | 0.606299 |
| 16 | ファルコンズ | 離れて | 25.3 | 22.6 | 2.7 | -144 | 0.590164 |
| 17 | バッカニアーズ | 家 | 30.35 | 19.05 | 11.3 | -458 | 0.820789 |
確率の列を積むと、5試合すべてに勝つ確率は0.163813になります。これは+510という妥当なラインに相当します。つまり、あなたが引用したラインはどちらも適切ではありません。
この質問は 、Wizard of Vegasの私のフォーラムで提起され、議論されました。
2015 年シーズン第 13 週のパンサーズ対セインツ戦前半の最後のプレーは何でしたか?
これは「ポイント・アフター・タッチダウン・リターン」と呼ばれるものだと思います。今シーズンから施行されたルール変更により、タッチダウン後のキックが失敗し、相手チームがタッチダウンを決めた場合、得点したチームに2点が加算されます。2015年シーズン以前は、デッドボールでした。これはNFLで初めて、そして今のところ唯一の、このような得点でした。YouTubeで動画をご覧いただけます。
この質問は、Wizard of Vegasの私のフォーラムで提起され、議論されました。
ご存知の通り、NCAAバスケットボール選手権で第16シードのUMBCが第1シードのバージニア大学を破りました。これは、現在の形式でのマーチマッドネスの34年の歴史において、前例のない出来事です。これは、パーフェクトブラケットが完成する確率にどのような影響を与えるのでしょうか。
この試合と2018年シーズンの他の試合全てを対象にモデルを調整した結果、パーフェクトブラケットの確率は42,743,890,552分の1となりました。私の戦略とこの数値に至った経緯については、「パーフェクトブラケットの確率」のページをご覧ください。
スポーツ賭博のオッズをアメリカ式とヨーロッパ式の間で変換するにはどうすればいいですか?
アメリカ式に表現されたオッズを a、ヨーロッパ式に表現されたオッズを e としましょう。
アメリカからヨーロッパへ移動するには:
a>0の場合、e=1+(a/100)となります。
a<0の場合、e=(a-100)/aとなります。
ヨーロッパからアメリカへ移行するには:
e>=2の場合、a=100×(e-1)となります。
e<2の場合、a=100/(1-e)となります。
ウィリアムヒルのスポーツブックで、メジャーリーグの試合でグランドスラムが達成されるかどうかを賭けるプロポジションベットを見ました。試合数に応じて、この賭けの妥当な確率とラインはどれくらいでしょうか?
他の読者のために、 2019年5月11日のグランドスラムの試合結果を掲載します。列の見出しは「ホーム」と「アウェイ」ではなく、「はい」と「いいえ」にしてください。

この疑問に答えるために、2011年から2018年までのMLB全試合を調べました。この8シーズンでは、19,440試合で858のグランドスラムが達成されました。つまり、1試合あたりのグランドスラム達成数の平均は0.0441となります。これは、ある試合でグランドスラムが達成される確率とは異なります。なぜなら、1試合で複数のグランドスラムが達成される可能性があるからです。ポアソン分布を用いると、ある試合で少なくとも1つのグランドスラムが達成される確率は4.3176%です。
この確率があれば、少なくとも 1 つのグランド スラムの確率と公平なラインをゲーム数ごとに示す次の表を簡単に作成できます。
グランドスラムの確率
| ゲーム | 確率 グランドスラム | フェアライン |
|---|---|---|
| 1 | 4.32% | 2216 |
| 2 | 8.45% | 1084 |
| 3 | 12.40% | 706 |
| 4 | 16.18% | 518 |
| 5 | 19.80% | 405 |
| 6 | 23.27% | 330 |
| 7 | 26.58% | 276 |
| 8 | 29.75% | 236 |
| 9 | 32.78% | 205 |
| 10 | 35.68% | 180 |
| 11 | 38.46% | 160 |
| 12 | 41.12% | 143 |
| 13 | 43.66% | 129 |
| 14 | 46.09% | 117 |
| 15 | 48.42% | 107 |
| 16 | 50.65% | -103 |
ただし、私の回答はMLBの平均値に基づいていることを付け加えておきます。特定の日においては、プレイヤーは実際に行われる試合数を考慮する必要があります。特に、オーバー/アンダーのラインが高いほど、グランドスラム達成の可能性が高くなります。
ニュージャージー州のMGMなど、多くのスポーツブックでは、真の無料ベットを提供しています。賭けが負けた場合、現金で返金され、その後出金できます。スロットの100%損失リベートをスポーツベッティングに適用したようなものです。このプロモーションではどのような賭けをすべきでしょうか?
このようなフリーロールでは、大金を狙うべきです。パーレーが許可されている場合は、プロモーションで許可されている金額まで賭け、ラスベガスでは通常約10万ドルの最高配当に達するまで十分なイベントをパーレーしましょう。
1 つのイベントに賭ける必要がある場合は、できるだけ大きな大穴を見つけてください。
この戦略がなぜ最善なのかを示す例として、同じプロモーションをダブルゼロルーレットで100ドル賭けた場合を考えてみましょう。イーブンマネーベットをした場合、期待される払い戻し額は(18/38)×200ドル + (20/38)×100ドル = 147.37ドルです。一方、シングルナンバーベットの場合は、(1/38)×3600ドル + (37/38)×100ドル = 192.11ドルになります。
オンラインスポーツブックで、NFLのマネーラインベットで、選択したチームが17点以上リードしている場合、自動的に勝ちと判定されるというプロモーションを見ました。この特典の価値はいくらですか?
このプロモーションでは、選択したチームが17点以上リードした後に負けた場合、本来なら負けになるはずの賭けが勝ちに変わります。良い例として、第51回スーパーボウルのアトランタ・ファルコンズへの賭けが挙げられます。第3クォーターのある時点で、ファルコンズは28対3と25点リードしていました。しかし、その後28対34で敗れました。
この疑問に答えるために、私は2000年から2015年までのNFLシーズン4,131試合を調査しました。以下の表は、試合中に勝利チームが抱えていた最大の点差を示しています。確率の列は、引き分けに終わった5試合を除外しています。
最大の赤字を克服
| 赤字 | ゲーム | 確率 |
|---|---|---|
| ネクタイ | 5 | 0.000000 |
| 0 | 1804 | 0.437227 |
| 1 | 100 | 0.024237 |
| 2 | 29 | 0.007029 |
| 3 | 560 | 0.135725 |
| 4 | 235 | 0.056956 |
| 5 | 23 | 0.005574 |
| 6 | 131 | 0.031750 |
| 7 | 622 | 0.150751 |
| 8 | 39 | 0.009452 |
| 9 | 34 | 0.008240 |
| 10 | 195 | 0.047261 |
| 11 | 84 | 0.020359 |
| 12 | 14 | 0.003393 |
| 13 | 49 | 0.011876 |
| 14 | 104 | 0.025206 |
| 15 | 10 | 0.002424 |
| 16 | 6 | 0.001454 |
| 17 | 36 | 0.008725 |
| 18 | 14 | 0.003393 |
| 19 | 2 | 0.000485 |
| 20 | 4 | 0.000969 |
| 21 | 22 | 0.005332 |
| 22 | 0 | 0.000000 |
| 23 | 2 | 0.000485 |
| 24 | 5 | 0.001212 |
| 25 | 1 | 0.000242 |
| 26 | 0 | 0.000000 |
| 27 | 0 | 0.000000 |
| 28 | 1 | 0.000242 |
| 合計 | 4131 | 1.000000 |
「引き分け」の行は、16シーズン中5試合が引き分けに終わったことを表すため、カウントしません。「0」の行は、勝利チームが一度も負けていなかった試合の43.7%を表します。
表を見ると、17点差以上で負けた後に勝利した試合が87試合あることがわかります。4126試合(引き分け5試合を除く)を合計すると、この確率は2.11%となります。
これらの状況では負けが勝ちに転じる可能性があるため、この確率を2倍にして4.22%とします。マネーラインベットのハウスエッジはスプレッドベットとほぼ同じ4.76%です。4.22%を差し引くと、このプロモーションではハウスエッジは0.54%と非常に低くなります。
マーチマッドネス 2023 が終了しましたが、完璧なブラケットの確率とシード別の予想勝利数はどのように変化しましたか?
完璧なブラケットを作るための私の戦略は、すべての試合でシード順の高いチーム(つまり、シード番号が低いチーム)を選ぶことです。最終的に1対1のシードになった場合は、ランダムに選びます。これは38シーズンのデータに基づいています。各試合の確率は以下のとおりです。
- 1位対16位 = 99.31%
- 2位対15位 = 93.06%
- 3位対14位 = 84.72%
- 4位対13位 = 78.47%
- 5位対12位 = 64.58%
- 6位対11位 = 62.50%
- 7位対10位シード = 60.42%
- 8位対9位 = 51.39%
1回戦を突破するには、上記の8試合すべてに4回ずつ勝つ必要があります。その確率は1/4354です。
この戦略を使用してここまで進んだ場合、第 2 ラウンドのさまざまな対戦は次のとおりです。
- 1対8シード = 80.00%
- 2位対7位 = 69.51%
- 3対6シード = 60.00%
- 4対5シード = 56.00%
2回戦を突破するには、上記の4つのゲームすべてにそれぞれ4回ずつ勝つ必要があります。その確率は1/811です。
この戦略を使用してここまで進んだ場合、第 3 ラウンドのさまざまな対戦は次のとおりです。
- 1位対4位 = 73.44%
- 2位対3位 = 60.71%
第2ラウンドに進むには、上記の2つのゲームをそれぞれ4回ずつ勝つ必要があります。その確率は1/54です。
第4ラウンドでは、1シード対2シードの対戦が行われます。1シードが勝つ確率は53.73%です。これが4回起こる確率は0.5373÷ 4 = 0.112355です。
第5ラウンドでは、1対1のゲームが2つ行われます。それぞれの勝率は1/2なので、2つ勝つ確率は1/4です。
第6ラウンドでは、1対1のゲームが1回行われます。勝率は1/2です。
これらすべての確率を積算すると、完全な括弧の確率は 13,569,150,522 分の 1 になります。
その他の質問にお答えするために、シード別のチームあたりの平均勝利数を以下に示します。
- 1シード = 平均3.29勝
- 2シード = 平均勝利数 2.32
- 3シード = 平均勝利数 1.85
- 4シード = 平均勝利数 1.55
- 5シード = 平均勝利数 1.16
- 6シード = 平均勝利数 1.07
- 7シード = 平均0.9勝
- 8シード = 平均勝利数 0.74
- 9シード = 平均勝利数 0.59
- 10シード = 平均勝利数 0.61
- 11シード = 平均勝利数 0.63
- 12シード = 平均勝利数 0.51
- 13シード = 平均勝利数 0.25
- 14シード = 平均勝利数 0.16
- 15シード = 平均勝利数 0.11
- 16シード = 平均勝利数0.01


