ビデオポーカー - 一般
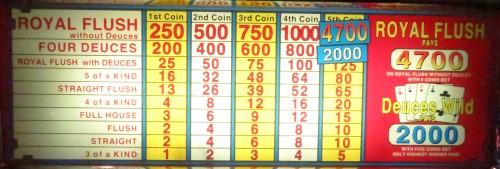
8/5ボーナスマシンをプレイしています。ロイヤルフラッシュで$1,199、8が4枚揃うとダブルボーナスに加え、2、3、4、Aが4枚揃うと通常のボーナススケジュールが適用されます。スロットカードと最大コインが必要です。これは100%以上ですか?
1199ドルという配当は面白い。カジノがIRS(内国歳入庁)に勝利金を報告する義務がある1200ドルの上限をわずかに下回っているのだ。Winpoker 6ソフトウェアは、カスタムデザインされたゲームの分析を可能にする。この場合、リターンは100.0079%となる。
ビデオポーカーは、ジャックまたはベターでも、ワイルドバージョンでも、実際のトランプのデッキのようにプレイできますか? つまり、マシン前面のペイオフスケジュールによって、そのマシンの正確なペイバックが決まるのでしょうか。それとも、コンピュータチップを使って内部をいじくり回し、ペイオフスケジュールを無意味にできるのでしょうか? 私は、Strictly Slots 誌の記事を読んで、それが可能だと知るまでは、これは不正だと考えていました。もしこれが本当なら、異なるハウスエッジを持つ 2 台の同一のビデオポーカー マシンを並べて設置できることになります。カジノではそれが可能であり、通常のスロット マシンでも同様です。もしこれが本当なら、私が長年雑誌、ソフトウェア、書籍で読んできたペイオフスケジュールの VP ペイバック率はすべて無意味になります。
信頼できるビデオポーカーマシンメーカーであれば、公正かつ正確なマシンを製造していると確信しています。不正なマシンやチップが存在する可能性はありますか?もちろんです。ご紹介いただいた記事、ぜひ読んでみたいです。
ギャンブルをする人々に無料でアドバイスを提供するという貴社の活動を、広告主が引き続き支援しているかを確認するため、広告主のウェブサイトを訪問しようと考えています。素晴らしいサイトですね。質問なのですが、ビデオポーカーで捨てられたカードと同じカードを引くことは可能でしょうか?ミシガン州ゲーミング管理委員会は、すべてのイベントは乱数発生器によって決定されるという、半分しか答えていません。次に、VPでペイアウトハンドが成立する確率は、同じく乱数発生器によって制御されるスロットマシンのように、カジノによる操作の影響を受けるのでしょうか?
ご支援ありがとうございます。バナーをクリックしてサイトを応援していただければ幸いです。ご質問にお答えすると、同じカードが戻ってくることはありません。マシンは単一のデッキから公平なディールを提示します。一度カードを捨てたら、そのカードは戻ってきません。2つ目の質問にお答えすると、カジノは各ハンドの確率を変更することはできません。ビデオポーカーマシンは公平なゲームをディールします。各ハンドがどのくらいの頻度で出るかは、カードのランダムなドローとあなたのプレイスキルによって決まります。
ミシシッピ州では、ビデオポーカーの法律はネバダ州と同じで、各ハンドは新しいゲームであるというのですか?
過去のハンドを記憶せずに、毎回新しいデッキから配られるのか、とお尋ねだと思います。ビデオポーカーは本来このようにプレイされるべきで、ミシシッピ州も例外ではないはずです。
インターネット新聞のコラムは6月以来更新されていません。大丈夫ですか?そうであることを願います。ブラックジャックの基本戦略カードを持っていて、とても役立っています。電子ポーカーゲームの基本戦略カードはありますか?お時間をいただきありがとうございました。
どのインターネット新聞のコラムのことを指しているのか分かりませんが、大丈夫です。実は、Custom Strategy Cards で私のビデオポーカー戦略をまとめた便利な戦略カードが手に入ります。ビデオポーカーカードはまだリストに載っていないかもしれませんが、店主が持っているはずなので、お気軽にお尋ねください。
更新: カスタム戦略カード事業はもう存在しません。
ウィザード様、最低払い戻し額に関する法律はビデオポーカーマシンにどのような影響を与えますか?理想的な戦略が不明な場合、カジノはVPマシンを設置できますか?州法で定められているように、ペイアウト率がx%を下回る戦略をとった場合、(ペイアウト率の高いペアやパットロイヤルでさえも捨てるような)非常に愚かなプレイヤーがカジノを訴えることはできますか?最後に、好奇心からお聞きしたいのですが、ロイヤルフラッシュを捨てたり、5枚のガベージハンドのカードをすべてキープしたりした場合など、VPマシンで可能な最低払い戻し額はどれくらいでしょうか?貴重なお時間を割いて読んでいただき、ご返信いただければ幸いです。
ネバダ州ゲーミング管理委員会規則14.040.1(a)では、ゲーミング機器はプレイヤーが最適な戦略をとった場合、少なくとも75%のリターンを返さなければならないと規定されています。2つ目の質問にお答えすると、私はビデオポーカーのプログラムを修正し、常に最悪のプレイをするようにしました。例えば、配当のないハンドの5枚すべてをキープし、パットハンドの一部または全部を捨てるというものです。ジャックス・オア・ベターが9/6の場合、この戦略ではリターンは2.72%、ハウスエッジは97.28%となります。以下は完全なリターン表です。このようなプレイヤーは、プレイが悪かったため、カジノを訴えることはできません。
ジャックス・オア・ベター - 最悪のプレイヤー
| 手 | 精算 | 番号 | 確率 | 戻る |
|---|---|---|---|---|
| ロイヤルフラッシュ | 800 | 48564 | 0.000000 | 0.000002 |
| ストレートフラッシュ | 50 | 2058000 | 0.000000 | 0.000005 |
| 4枚揃い | 25 | 38040380 | 0.000002 | 0.000048 |
| フルハウス | 9 | 292922028 | 0.000015 | 0.000132 |
| フラッシュ | 6 | 336550092 | 0.000017 | 0.000101 |
| 真っ直ぐ | 4 | 6239759724 | 0.000313 | 0.001252 |
| 3つ揃い | 3 | 12510891616 | 0.000628 | 0.001883 |
| 2組 | 2 | 34968642984 | 0.001754 | 0.003509 |
| ジャック以上 | 1 | 334574728656 | 0.016785 | 0.016785 |
| 何もない | 0 | 19544266875156 | 0.980487 | 0.000000 |
| 合計 | 19933230517200 | 1.000000 | 0.023717 |
オンラインで練習するためにビデオポーカー ゲームを 1 つ選ぶとしたら (ラスベガスにいるときにプレイ方法を知るために)、それは何ですか。
必要なものはすべてここにあります!
間違いを犯したときに訂正してくれるビデオポーカー ゲームもあります。
あらゆるハンドをどのようにプレイするかを分析するためのハンド アナライザーがあります。
あらゆるゲームのリターンとペイテーブルを決定するためのゲーム リターン計算機があります。
最後に、あらゆるゲームの戦略を作成するための戦略メーカーがあります。
注: この回答は 2013 年 11 月 13 日に更新されました。
98% の還元率を誇るビデオ ポーカー マシンに 100 ドル札を入れて破産するまでプレイした場合、合計で平均していくら賭けることになりますか?
この答えは簡単な公式で表せます。初期投資額をハウスエッジで割るのです。この場合、答えは100ドル/0.02 = 5000ドルです。しかし、ビデオポーカーのボラティリティが高いため、ほとんどの場合、100ドルはそれほど長くは持ちません。
世界最悪のビデオポーカーマシンを抱えるコネチカット州の人たちに何かアドバイスはありますか?市場が必ずしもそれを求めていないのに、カジノに品揃えを改善するよう圧力をかける、認められた方法はあるのでしょうか?
競争がほとんどない環境では、こういうことが起こります。カジノにもっと良いマシンを求めても無駄です。プレイヤーがひどいペイテーブルでゲームをプレイするなら、一体なぜカジノ側が何かを変える必要があるのでしょうか? 唯一の望みは、コネチカット州の議員に手紙を書いて、州内のギャンブルにおける2つのカジノの独占状態を終わらせ、他のカジノが競争できるようにするよう要請することだけです。
1プレイあたり50ドルでプレイする場合、以下の2つのビデオポーカーゲームのうち、どちらを選びますか?(両方のゲームの支払いスケジュールが同じで、1ハンドあたり最大5コインを賭けると仮定)10ドルのシングルプレイと1ハンドあたり1ドルのテンプレイ。お時間をいただき、ご検討いただきありがとうございます。
数学的には期待リターンは同じです。しかし、私は10プレイを選びます。ボラティリティが低く、より楽しいと思うからです。
無料のオンラインビデオポーカーゲームはたくさんあります。しかし、インターネットに接続せずにプレイできるバージョンを探しています。Jacks or Betterの無料ダウンロード版で、インターネットを使わずにプレイできるものをご存知でしょうか?無料のデモ版もいくつか見つけたのですが、ゲームはローカルでロードされているにもかかわらず、プレイ中にサイトに接続してしまいます。基本的な機能だけで十分で、リアルなバージョンがあれば嬉しいです。よろしくお願いします。
Winpokerの無料デモ版なら、期限切れなしで使えると思います。ダウンロードはwww.zamzone.comから可能です。
ビデオポーカーの歪度係数とは何ですか?
他の読者のために、あらゆる確率変数の歪度係数(歪度)とは、どちらの方向の裾が長いかを示す指標です。負の歪度は、最も起こりやすい結果が分布の上限側にあり、極端な結果が下限側に偏る傾向があることを意味します。正の歪度はその逆で、最も起こりやすい結果は下限側にありますが、極端な結果が上限側に偏る傾向があります。負の歪度では平均値は中央値より小さくなり、正の歪度では平均値は中央値より大きくなります。正確な計算式はWikipediaや多くの統計書籍で見つけることができます。
大まかに言えば、歪度は1回のセッションでどれだけの頻度で勝利を得られるかと相関関係にあります。ジャックス・オア・ベターでは、ロイヤルが出ない限り、数時間で勝利セッションを得ることはまずありません。一方、ダブル・ダブル・ボーナスでは、高額の4倍の配当があるため、数時間プレイすれば勝利する可能性が高くなります。ほとんどの人は認知バイアスの影響を受けやすいため、負けたときの痛みは勝利したときの喜びの2倍です。人々がダブル・ダブル・ボーナスをプレイするのは、その変動性を好むからではなく、勝つ可能性が高くなるからです。次の表は、一般的な4つのビデオポーカーゲームの主要な統計情報を示しています。ジャックス・オア・ベターで歪度が最も大きいのは興味深い点です。
主要なビデオポーカー統計
| 統計 | ジョブB — 9/6 | BP — 8/5 | DDB — 9/6 | DW — NSUD |
|---|---|---|---|---|
| 戻る | 0.995439 | 0.99166 | 0.989808 | 0.997283 |
| 分散 | 19.514676 | 20.904113 | 41.985037 | 25.780267 |
| スキュー | 147.114643 | 134.412152 | 66.495372 | 101.23991 |
| (過剰)尖度 | 26,498 | 23,202 | 6,679 | 14,550 |
JoB — 9/6 =ジャックス・オア・ベターのフルペイ
BP — 8/5 = 標準配当ボーナスポーカー
DDB — 9/6 = 標準配当ダブルダブルボーナスポーカー
DW — NSUD = 「それほど醜いアヒルではない」デュース・ワイルド
これを知ることで、ビデオポーカープレイヤーは実際にどう役立つのでしょうか?おそらく、スキューの大きいゲームは、数時間のセッションで負ける可能性が高くなると言えるでしょう。例えば、ジャックス・オア・ベターでは、ロイヤルが出なければ、ハウスエッジによって最終的に資金が減っていくでしょう。しかし、デュース・ワイルドやダブル・ダブル・ボーナスのようなゲームでは、2番目に高い勝ち金がセッション中に窮地から脱出できる可能性があります。つまり、スキューはロイヤルが出ないときに勝てないようにするのです。スキューを知っても勝率は上がりませんが、何が起こるかを知っておくことは精神的に役立ちます。ですから、次に9/6ジャックスで負けたときは、スキューのせいにしましょう。
この質問にご協力いただいた Jeff B. に感謝します。
アトランティックシティでビデオポーカーをプレイしていたのですが、ドローで捨てたカードと同じカードが出てくることが時々ありました。もしマシンが捨てたカードをデッキに戻していたら、オッズにどのような影響があるのでしょうか?
Cryptologicのインターネットカジノには、ボーナスビデオポーカーと呼ばれるゲームがあり、捨て札をデッキに戻します。このゲームの40-20-9-6ジャックス・オア・ベターの配当表は、リドローボーナス機能(ここでは説明しません)を考慮する前で95.2642%の配当となります。従来のビデオポーカーでは、この配当表は98.2534%の配当となります。つまり、この例では、捨て札をデッキに戻すことでプレイヤーはほぼ3%の損失を被ることになります。しかし、アトランティックシティのマシンで実際にこのようなことが起こったとは到底考えられません。
この質問は、私の関連サイトであるWizard of Vegasのフォーラムで提起され、議論されました。
ロイヤルを獲得するチャンスが最も高いビデオポーカー ゲームはどれですか?
まずは、シンプルなビデオポーカーゲームを見てみましょう。以下の表は、ロイヤルの確率を高い順から低い順に示しています。この表にはワイルドロイヤルは含まれていません。ワイルドロイヤルはナチュラルよりもはるかに配当が低くなります。
ビデオポーカーロイヤルの確率
| ゲーム | 確率 | 逆 |
|---|---|---|
| 17-7 ジョーカーポーカー | 0.0000259892 | 38,478 |
| 8-5ボーナスポーカー | 0.0000248551 | 40,233 |
| 9-6 ジャックス | 0.0000247583 | 40,391 |
| 9-6 ダブルダブルボーナス | 0.0000245102 | 40,799 |
| 9-6 ボーナスポーカー デラックス | 0.0000237661 | 42,077 |
| 「フルペイ」デュースワイルド | 0.0000220839 | 45,282 |
| 10-7 ダブルボーナス | 0.0000208125 | 48,048 |
驚いたことに、ジョーカーポーカーはナチュラルロイヤルになる可能性が最も高いです。これは、ナチュラルロイヤルを作るために使えない余分なカードがあるにもかかわらず、驚きです。
次に、非標準のビデオポーカー ゲームをいくつか見てみましょう。
9-6 ジャックスロイヤルドローでは、オッズは 12,178 分の 1 です。
7-5ジャックス・セカンドチャンスロイヤルのオッズは10,827分の1です。これには200ドルのみ支払われる「セカンドチャンス」ロイヤルも含まれます。
最後に、トリプルダブルボーナスについても触れておきたいと思います。4枚のエースと2~4のキッカーの組み合わせは、ロイヤルフラッシュと同じ1コインあたり800の配当となります。9~7の配当表に基づくと、800の配当は10,823分の1です。さらに魅力的なのがロイヤルエースボーナスポーカーで、ロイヤルフラッシュまたは4枚のエースの組み合わせで800の配当となり、800の配当は3,673分の1の確率です。
しかし、総合的に判断すると、最もナチュラルロイヤルが出るゲームは「チェイス・ザ・ロイヤル」です。9-6ジャックスのペイテーブルに基づくと、ロイヤルフラッシュの確率は9,084分の1です。
ビデオポーカーの合計組み合わせとして、19,933,230,517,200 という数字が頻繁に出てくるのはなぜですか?
他の読者のために、9-6 Jacks or Better のリターン テーブルを以下に示します。
「9-6」ジャックス・オア・ベター
| 手 | 精算 | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| ロイヤルフラッシュ | 800 | 493512264 | 0.00002476 | 0.01980661 |
| ストレートフラッシュ | 50 | 2178883296 | 0.00010931 | 0.00546545 |
| フォー・オブ・ア・カインド | 25 | 47093167764 | 0.00236255 | 0.05906364 |
| フルハウス | 9 | 229475482596 | 0.01151221 | 0.10360987 |
| フラッシュ | 6 | 219554786160 | 0.01101451 | 0.06608707 |
| 真っ直ぐ | 4 | 223837565784 | 0.01122937 | 0.04491747 |
| スリーオブアカインド | 3 | 1484003070324 | 0.07444870 | 0.22334610 |
| 2組 | 2 | 2576946164148 | 0.12927890 | 0.25855780 |
| ジャックス・オア・ベター | 1 | 4277372890968 | 0.21458503 | 0.21458503 |
| 何もない | 0 | 10872274993896 | 0.54543467 | 0 |
| 合計 | 19933230517200 | 1 | 0.99543904 |
私のビデオ ポーカーの 52 枚のカード ゲームのリターン テーブルのほとんどは、19933230517200 という同じ数の組み合わせを持っています。なぜでしょうか?
まず、52 枚の中から 5 枚のカードを選ぶ方法はcombin (52,5) = 2,598,960 通りあります。
次に、プレイヤーが捨てるカードの枚数に応じて、ドローの組み合わせは最大でcombin(47,5) = 1,533,939通りあります。次の表は、2列目に捨てるカードの枚数に応じたドローの組み合わせの数を示しています。
ドローの組み合わせ
| 破棄 | 組み合わせ | 重さ | 製品 |
|---|---|---|---|
| 0 | 1 | 7,669,695 | 7,669,695 |
| 1 | 47 | 163,185 | 7,669,695 |
| 2 | 1,081 | 7,095 | 7,669,695 |
| 3 | 16,215 | 473 | 7,669,695 |
| 4 | 178,365 | 43 | 7,669,695 |
| 5 | 1,533,939 | 5 | 7,669,695 |
2列目の数字の最小公倍数は7,669,695です。この数は5×combin(47,5)と表すことができます。すべてのハンドの組み合わせの総数を一定に保つため、ドローの組み合わせに重み付けを行い、ドローの組み合わせの総数が7,669,695になるようにします。
つまり、19,933,230,517,200 = combin(52,5)×combin(47,5)×5 となります。私が使用している52枚のビデオポーカーテーブルの中には、組み合わせの数が少ないものもあります。これは、最終的なリターンテーブルにおける各ハンドの組み合わせの合計数の最大公約数が1より大きい場合があるためです。このような場合、各合計数を最大公約数で割ることがあります。私のビデオポーカーアナライザーはこれを自動的に行っています。
この質問は私のWizard of Vegasフォーラムで提起され、議論されました。
Dカジノが101.60%ルーズデュースゲームを廃止したというのは本当ですか?確か、あれはラスベガスで最もルーズなビデオポーカーマシンだと言っていたような気がします。もし噂が本当なら、今一番人気なのはどのマシンですか?
はい、そのマシンはもうありません。ご指摘の通り、以前は2位だったゲームが、今では1位に躍り出ています。エル・コルテスのダブルデュースゲームは配当100.92%です。ペイテーブルは940-400-25-16-13-4-3-2-2-1です。カジノの北端にある、古いカソードローマシンが並ぶスロットルームで見つけることができます。私がその横に立っている写真がこちらです。

ご参考までに、Loose Deuces と Double Deuces の違いは、前者は 4 つの 2 に対して 500 が支払われ、後者は 400 が支払われることです。
ビデオポーカーでは、2つのプレイがベストプレイと同じくらい良いハンドがあることは知っています。例えば、フルペイのデュースワイルドでツーペアが成立した場合、プレイヤーは1つのペアだけをキープするべきで、どのペアでも構いません。質問なのですが、3つのプレイがベストプレイと同じくらい良いハンドがある状況はあるのでしょうか?
はい!ジョーカーポーカーでは、ガベージハンドの場合、一般的には、ドローでストレートまたはフラッシュを形成する可能性が最も高いミドルカードを1枚キープするのが最善です。しかし、時にはどのカードを保持するのが最善か、判断が難しい場合や、引き分けになる場合もあります。
例えば、ジョーカー・ツーペアとQh、10d、5d、7c、2cのドローの配当表(97.19%)では、10d、5d、7cのみを保持するのがベストプレイで、3つ全て保持した場合の期待値は0.240703です。これは、私のビデオポーカーハンドアナライザーを使って検証できます。
同じジョーカー ポーカーのペイ テーブルでのその他のプレイは次のとおりです。
- QC 10S 5D 7H 2C
- クイックH 10D 5D 7H 2C
- KH 10D 5D 8C 3C
- KC 10S 5D 8H 3C
- KH 10D 5D 8H 3C
この質問にご協力いただいた Gary Koehler 氏に感謝します。
こんにちは。ビデオポーカーの大ファンなので、このメールを書いています(ただし、ギャンブラーではなく、あくまでシミュレーションで楽しむためにプレイしています)。いくつかシミュレーションを試してみたかったのですが、あなたの「ビデオポーカー分析のための私の方法論」というページが非常に役に立ちました。実際に理解するまでに何度か試行錯誤しましたが、最終的にはゲームを自動プレイする小さなシミュレーターを書くことができました。その結果をあなたの「ビデオポーカーハンドアナライザー」のページと照らし合わせても、同じ答えが得られるようになりました。
しかし、方法論のページは、ワイルドカードを含まない標準的な52枚のカードデッキのみを扱っています。私は独自にアルゴリズムを拡張し、デッキにジョーカーを1枚から4枚追加できるようにしてみましたが、今のところ結果は遅く、不正確です。問題の一つは、私のアルゴリズムではワイルドカードの代わりに52通りの可能性を代入するため、ワイルドカードによって複雑さが増すように見えることです。さらに、アルゴリズムではインデックスの重複は許可されていないと思います。方法論のページを拡張して、標準的なデッキと同様に効率的にワイルドカードの状況に対処するためのヒントを提供できるようにできないかと考えています。
このウェブサイトは大変気に入っています。これまでサポートしていただき、本当に感謝しています。このウェブサイトがなければ、プロジェクトを完了することはできなかったと思います。良い一日をお過ごしください!
温かいお言葉をありがとうございます!
ワイルドカードの使い方を52通りすべて試すのは、特にワイルドカードが複数ある場合は間違いなく時間がかかります。ワイルドカードを使ったハンドのスコアリング方法は以下の通りです。
- ナチュラルロイヤルフラッシュを持っている場合は、そのハンドをそのようにスコアします。
- それ以外の場合は、手札にあるワイルドカードの数を数えます。
- 次に、この数字と他のカードの値に応じてハンドにスコアを付けます。
例えば、ワイルドカードが2枚あるとします。次の擬似コードを使って、残りの3枚のカードに基づいてハンドのスコアを計算することができます。
- 3 枚のカードが同じスーツで、最も低いカードが 10 以上の場合、ワイルド ロイヤルとなります。
- それ以外の場合、3 枚のカードが同じスーツで、最高と最低の差が 4 以下の場合は、ストレート フラッシュになります。
- それ以外の場合、3 枚のカードが同じスーツで、最も高い数字がエースであり、2 番目に高い数字が 5 以下である場合も、ストレート フラッシュ (A2345) となります。
- そうでなければ、ペアがあれば、フォー・オブ・ア・カインドになります。
- そうでなければ、3 枚のカードが同じスーツであれば、フラッシュになります。
- それ以外の場合、最高値と最低値の差が 4 以下の場合は、ストレートになります。
- それ以外の場合、最も高い数字がエースで、2 番目に高い数字が 5 以下の場合も、ストレートになります (A2345)。
- そうでなければ、ペアになります。
ワイルドなしのコードは既にあるため、デュースとジョーカー ワイルドを分析するかどうかに応じて、1 個から 4 個または 5 個のワイルド用の別個のコードを作成する必要があります。
13ランクすべてでフォーカードを達成するとボーナスが支払われるプロモーションを知っています。平均して何ハンドかかりますか?
あなたの質問に答えるために、ビデオポーカーのゴールドスタンダードである「9-6ジャックス オア ベター」を見てみましょう。
最初のステップは、計算機を改造して、13種類のフォー・オブ・ア・カインドすべてに対応する項目を追加することです。改造後のリターン表は以下のとおりです。
修正されたジャックス・オア・ベターのリターンテーブル
| イベント | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| ロイヤルフラッシュ | 800 | 4億9351万2264円 | 0.000025 | 0.019807 |
| ストレートフラッシュ | 50 | 2,178,883,296 | 0.000109 | 0.005465 |
| 4A | 25 | 3,900,253,596 | 0.000196 | 0.004892 |
| 4K | 25 | 3,904,533,816 | 0.000196 | 0.004897 |
| 4つのQ | 25 | 3,898,370,196 | 0.000196 | 0.004889 |
| 4つのJ | 25 | 3,886,872,684 | 0.000195 | 0.004875 |
| 4 10 | 25 | 3,471,687,732 | 0.000174 | 0.004354 |
| 4つの9 | 25 | 3,503,226,684 | 0.000176 | 0.004394 |
| 4つの8 | 25 | 3,504,128,652 | 0.000176 | 0.004395 |
| 4 7 | 25 | 3,504,825,252 | 0.000176 | 0.004396 |
| 4 6 | 25 | 3,504,861,888 | 0.000176 | 0.004396 |
| 4 5 | 25 | 3,504,895,944 | 0.000176 | 0.004396 |
| 4 4 | 25 | 3,504,032,676 | 0.000176 | 0.004395 |
| 4 3 | 25 | 3,503,177,148 | 0.000176 | 0.004394 |
| 4 2 | 25 | 3,502,301,496 | 0.000176 | 0.004393 |
| フルハウス | 9 | 229,475,482,596 | 0.011512 | 0.103610 |
| フラッシュ | 6 | 219,554,786,160 | 0.011015 | 0.066087 |
| 真っ直ぐ | 4 | 223,837,565,784 | 0.011229 | 0.044917 |
| スリーオブアカインド | 3 | 1,484,003,070,324 | 0.074449 | 0.223346 |
| 2組 | 2 | 2,576,946,164,148 | 0.129279 | 0.258558 |
| ジャック以上 | 1 | 4,277,372,890,968 | 0.214585 | 0.214585 |
| 何もない | 0 | 10,872,274,993,896 | 0.545435 | 0.000000 |
| 合計 | 19,933,230,517,200 | 1.000000 | 0.995439 |
フォー・オブ・ア・カインドが出る確率は 0.002363 です。
次に答えなければならないのは、13種類全て揃えるには平均して何回のフォー・オブ・ア・カインドが必要かということです。この質問に答えるために、期待試行回数計算機を作成しました。この計算機を使うには、最初の13個のセルに各フォー・オブ・ア・カインドの組み合わせの数を入力します。計算機は、13種類全て揃えるには平均で41.532646回のフォー・オブ・ア・カインドが必要であると計算します。
したがって、13 枚のフォー・オブ・ア・カインドすべてを獲得するために必要なハンドの予想数は、41.341739/0.002363 = 17,580 です。
8-5ボーナスポーカーを例に考えてみましょう。次の表は、賭けたライン数ごとのリターンを示しています。
- 4行: 99.375%
- 3行: 99.279%
- 2行目: 99.214%
- 1行目: 99.166%
次のリストは、プレイされるライン数に応じて、最大ラインをプレイしない場合のコストを示しています。
- 4行: 0.000%
- 3行目: 0.095%
- 2行目: 0.160%
- 1行目: 0.209%
ドリームカードビデオポーカーでは、ボーナスポーカーで配られる4枚のカードがすべてシングルトン5枚で、最低ランクが4、残りの3枚がすべてジャック未満で、ストレートやフラッシュのチャンスがない場合、正しいドリームカードが出ないことをご存知ですか? 4枚の4がプレミアム勝利となるため、正しいドリームカードは4です。しかし、配られるドリームカードは他のランクのカードになります。プレイヤーが常にこの間違ったドリームカードを受け入れると仮定した場合、そのコストはいくらになるでしょうか?
はい、その点は承知していました。他の読者の方々のために補足すると、ドリームカードでは、ランダムに配られた最初の4枚のカードに基づいて、5枚目に最適なカードが提示されることがあります。ボーナスポーカーでドリームカードが出る確率は46.7%です。プレイヤーは提示されたドリームカードを拒否し、デッキに残っている他のカードに切り替えることができます。ただし、私の知る限り、このアドバイスは常に正しいです。ただし、ボーナスポーカーの場合は例外です。
プレイヤーがドリームカードを引く場合、他の4枚のカードがこの状況になる確率は1.49%です。ドリームカードの確率が46.7%であることを考えると、この状況は0.70%、つまり144ハンドに1回発生します。
私のビデオポーカーハンドアナライザーを使うと、8/5ボーナスポーカーにおける4のペアの期待値は0.855134です。5と10のペアの期待値は0.813506です。つまり、プレイヤーがドリームカードを受け入れると仮定すると、バグが発生するたびに発生するコストは期待値で0.041628になります。
ゲームのリターンにかかる全体的なコストは 0.006955 × 0.041628 = 0.000290、つまり約 0.03% になります。
プレイヤーが常にロイヤルフラッシュを引いた場合、ロイヤルフラッシュが出る確率はどれくらいでしょうか?プレイヤーが常にロイヤルフラッシュになるカードが最も多いスーツを選ぶと仮定します。
次の表は、プレーヤーが常にロイヤルに最も多くのカードがあるスーツを選択することを前提として、ディールでロイヤルに 0 ~ 5 枚のカードがある確率、ロイヤルが完成する確率、および製品を示しています。
ロイヤル・オア・ナッシング・プレイヤー
| ロイヤルカード 取引について | 取引 確率 | 確率 コンプリートロイヤル | 製品 |
|---|---|---|---|
| 0 | 0.61538462 | 0.00000261 | 0.00000160 |
| 1 | 0.35444947 | 0.00003064 | 0.00001086 |
| 2 | 0.02835596 | 0.00070472 | 0.00001998 |
| 3 | 0.00173608 | 0.01057082 | 0.00001835 |
| 4 | 0.00007234 | 0.11627907 | 0.00000841 |
| 5 | 0.00000154 | 1.00000000 | 0.00000154 |
| 合計 | 1.00000000 | 0.00006075 |
右下のセルには、「ロイヤル・オア・ナッシング」のプレイヤーがロイヤル・フラッシュを作る確率が 0.000006075、つまり 16,461 分の 1 であることを示しています。
プレイヤーが次のカードを事前に見ることができる場合、ビデオポーカーでロイヤルフラッシュが出る確率はどれくらいでしょうか?
ゲームがランダムに5枚のカードを選び、プレイヤーが捨てるのを待つキューに並べると仮定しましょう。例えば、プレイヤーが3枚捨てた場合、キュー内の次の3枚を受け取ります。ちなみに、配られたカードに特定のカードが割り当てられていて、それが配られたカードのそれぞれに該当する場合も、答えは同じです。以下の表は、配られたカードで各数字がロイヤルに保持される確率、配られたカードでロイヤルが完成する確率、そしてその積を示しています。右下のセルは、全体の確率が0.00006075、つまり16,461分の1であることを示しています。
ビデオポーカーのパーフェクトピーカー
| ロイヤルカード 取引について | 取引 確率 | 確率 コンプリートロイヤル | 製品 |
|---|---|---|---|
| 0 | 0.61538462 | 0.00000261 | 0.00000160 |
| 1 | 0.35444947 | 0.00003064 | 0.00001086 |
| 2 | 0.02835596 | 0.00070472 | 0.00001998 |
| 3 | 0.00173608 | 0.01057082 | 0.00001835 |
| 4 | 0.00007234 | 0.11627907 | 0.00000841 |
| 5 | 0.00000154 | 1.00000000 | 0.00000154 |
| 合計 | 1.00000000 | 0.00006075 |
聞くところによると、妖精が現れて、ドローの手札を運命づけられたものに変えてしまうらしい。例えば、ディールで2枚の2が手札に残り、ドロー後に4枚の2に増える運命だったとしよう。もし2を捨てれば、ドローで残りの2枚は自然に手札に残るだろう。そして妖精は、捨てた2枚の2を2のジャンクカード2枚に変えるのだそうだ。
ビデオ ポーカーでは、配られた後にプレイヤーがロイヤルに対して 0 から 5 枚のカードを持つ頻度はどのくらいですか?
答えはかなり複雑です。なぜなら、配られた後、複数のスーツにおいて、プレイヤーがロイヤルの可能性を持つ方法はいくつかあるからです。プレイヤーは常にロイヤルの可能性が最も高いスーツのカードを保持し、ロイヤルの可能性が最も高いスーツが2つ以上ある場合は、任意にカードを選ぶと仮定します。さて、ここでいくつかの略語を定義しておきましょう。
- ロイヤルカード = ランク 10 からエースのカード。
- H = ハートのロイヤルカード。
- S = ハートのロイヤルカード。
- C = ハートのロイヤルカード。
- D = ハートのロイヤルカード。
- x = 非ロイヤルカード
以下の表は、あらゆる状況の組み合わせの数を示しています。各行には、数学的に同等なすべてのケースが含まれます。例えば、Hxxxx は、ハートだけでなく、どのスーツでもロイヤルのカードが1枚だけある場合を含みます。
ディール後のロイヤルへの組み合わせ
| 手 | ロイヤルカード | 組み合わせ |
|---|---|---|
| うーん | 5 | 4 |
| HHHHS | 4 | 300 |
| HHHHx | 4 | 640 |
| HHHSS | 3 | 1,200 |
| HHHSC | 3 | 3,000 |
| HHHSx | 3 | 19,200 |
| HHHxx | 3 | 19,840 |
| HHSSC | 2 | 6,000 |
| HHSSx | 2 | 19,200 |
| 保健福祉省 | 2 | 5,000 |
| HHSCx | 2 | 96,000 |
| HHSxx | 2 | 297,600 |
| HHxxx | 2 | 198,400 |
| HSCDx | 1 | 2万 |
| HSCxx | 1 | 24万8000 |
| HSxxx | 1 | 744,000 |
| Hxxxx | 1 | 719,200 |
| xxxxx | 0 | 201,376 |
| 合計 | 2,598,960 |
次の表は、配られた後にロイヤルに 0 ~ 5 枚のカードが渡される全体的な確率を示しています。
カードからロイヤルまでの確率
| ロイヤルカード | 確率 |
|---|---|
| 5 | 0.0002% |
| 4 | 0.0362% |
| 3 | 1.6637% |
| 2 | 23.9403% |
| 1 | 66.6113% |
| 0 | 7.7483% |
| 合計 | 100.0000% |
質問されたわけではありませんが、プレイヤーが「ロイヤルかナッシングか」の戦略に従った場合、1 ハンドあたりのロイヤルの確率は 23,162 分の 1 になります。
ビデオポーカーのプレイに完璧な賭け戦略を使用する場合、ロイヤルフラッシュを獲得するチャンスが最も高いのはどのゲームですか?
比較の基準として、従来のビデオポーカーでロイヤルフラッシュが出る確率は、最適な戦略を前提とした場合、約4万分の1から4万5千分の1程度です。ランダムに選んだいくつかのゲームにおける正確な数値を以下に示します。
- 9-6 ジャック以上: 40,391 分の 1
- 25-15-9-4-4-3(イリノイ)デュース・ワイルド— 43,423分の1
- 9-7トリプルダブルボーナス:45,358分の1
ロイヤルに飢えたプレイヤーにとって、 Chase the Royalでは確率が大幅に上がります。これはビデオポーカーの初期のバリエーションで、プレイヤーはディールで配られた絵札のペアを 3 枚のロイヤル フラッシュに交換できます。交換する価値を高めるために、ゲームでは、切り替えるとストレートとフラッシュの勝ちを引き上げます。ロイヤルの正確な確率は、ベース ゲームとペイ テーブルによって異なります。確率は、トリプル ボーナスのベース ゲームと 8-5 ペイ テーブルで、ロイヤル頻度が 9,151 分の 1 の場合に最大になります。これには、1 枚につき 800 を支払うドローのロイヤル (頻度は 9,282 分の 1) と、1 枚につき 2000 を支払うディール (頻度は 649,773 分の 1) の両方が含まれます。
しかし、フィーチャーを有効にするためにプレイヤーが基本ベット額と同額の手数料を支払う必要があるゲームを考えると、このゲームはさらに魅力的になります。ドリームカード付きドローポーカー(ドリームカードポーカーとは異なります)では、プレイヤーは5枚目のカードとして夢のカード(夢を見ているのは数学者だと仮定)を引くことがよくあります。ドリームカードの確率はジャックス・オア・ベターで最大となり、50.5%に達します。9-6ジャックス・オア・ベターでは、ロイヤルの出現頻度は8,105分の1です。フィーチャーを有効にする手数料を考慮すると、ロイヤルの実質的な勝利は1対400に低下することを覚えておいてください。
ドリームカードポーカー(ドリームカードを使ったドローポーカーとは別のゲーム)について言えば、このゲームにおけるロイヤルの出現頻度はそれほど高くありません。最も高いのは11-8-6ジャックス・オア・ベターで、15,034分の1の確率です。
この回答では、 Movin' On Up Poker は考慮していません。これは古くてあまり知られていないビデオポーカーゲームで、プレイヤーは1回ではなく2回または3回のドローを獲得します。このゲームにおけるロイヤルの出現頻度はわかりませんが、トリプルドローでは、プレイヤーは基本ベット額の5倍の手数料を支払うことで2回のドローを獲得するため、おおよそ4,000分の1程度と推定されます。
結論として、プレイヤーが何らかのギミックを有効にするために追加料金を支払わなければならないゲームを除けば、私の答えは Chase the Royal です。
イリノイ・デュースの「Not so Ugly Ducks」に最適な戦略でプレイした場合、プレイヤーのエラーにかかるコストはどれくらいですか?
ご参考までに、記載されている支払い表は次のとおりです。
それほど醜いアヒルではない: 1-2-3-4-4-10-16-25-200-800。
イリノイ デュース: 1-2-3-4-4-9-15-25-200-800
次に、このゲームの最適戦略に従った「Not so Ugly Ducks」のリターン テーブルを示します。
それほど醜いアヒルではない――正しい戦略
| イベント | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| ナチュラルロイヤルフラッシュ | 800 | 458,696,304 | 0.000023 | 0.018409 |
| 4つのデュース | 200 | 3,721,737,204 | 0.000187 | 0.037342 |
| ワイルドロイヤルフラッシュ | 25 | 38,006,962,464 | 0.001907 | 0.047668 |
| 5枚の同じもの | 16 | 61,961,233,656 | 0.003108 | 0.049735 |
| ストレートフラッシュ | 10 | 102,392,435,976 | 0.005137 | 0.051368 |
| フォー・オブ・ア・カインド | 4 | 1,216,681,289,508 | 0.061038 | 0.244151 |
| フルハウス | 4 | 520,566,943,104 | 0.026116 | 0.104462 |
| フラッシュ | 3 | 413,870,908,056 | 0.020763 | 0.062289 |
| 真っ直ぐ | 2 | 1,142,885,476,800 | 0.057336 | 0.114671 |
| スリーオブアカインド | 1 | 5,325,911,611,716 | 0.267188 | 0.267188 |
| 何もない | 0 | 11,106,773,222,412 | 0.557199 | 0.000000 |
| 合計 | 19,933,230,517,200 | 1.000000 | 0.997283 |
次に、イリノイ・デュースの配当表を示します。この配当表に適した戦略を使用しています。右下のセルには、配当が0.989131と表示されています。
イリノイ・デュース - 正しい戦略
| イベント | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| ナチュラルロイヤルフラッシュ | 800 | 459,049,128 | 0.000023 | 0.018423 |
| 4つのデュース | 200 | 3,727,422,492 | 0.000187 | 0.037399 |
| ワイルドロイヤルフラッシュ | 25 | 38,117,987,136 | 0.001912 | 0.047807 |
| 5枚の同じもの | 15 | 62,201,557,608 | 0.003120 | 0.046807 |
| ストレートフラッシュ | 9 | 98,365,859,016 | 0.004935 | 0.044413 |
| フォー・オブ・ア・カインド | 4 | 1,221,942,888,444 | 0.061302 | 0.245207 |
| フルハウス | 4 | 522,030,131,520 | 0.026189 | 0.104756 |
| フラッシュ | 3 | 407,586,633,720 | 0.020448 | 0.061343 |
| 真っ直ぐ | 2 | 1,145,767,137,120 | 0.057480 | 0.114961 |
| スリーオブアカインド | 1 | 5,342,397,992,292 | 0.268015 | 0.268015 |
| 何もない | 0 | 11,090,633,858,724 | 0.556389 | 0.000000 |
| 合計 | 19,933,230,517,200 | 1.000000 | 0.989131 |
次の表は、Not so Ugly Ducksの組み合わせと確率をIllinois Deucesのペイテーブルに使用したリターン表です。右下のセルには、リターンが0.989131と表示されています。
イリノイ デュース -- NSUD 戦略
| イベント | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| ナチュラルロイヤルフラッシュ | 800 | 458,696,304 | 0.000023 | 0.018409 |
| 4つのデュース | 200 | 3,721,737,204 | 0.000187 | 0.037342 |
| ワイルドロイヤルフラッシュ | 25 | 38,006,962,464 | 0.001907 | 0.047668 |
| 5枚の同じもの | 15 | 61,961,233,656 | 0.003108 | 0.046627 |
| ストレートフラッシュ | 9 | 102,392,435,976 | 0.005137 | 0.046231 |
| フォー・オブ・ア・カインド | 4 | 1,216,681,289,508 | 0.061038 | 0.244151 |
| フルハウス | 4 | 520,566,943,104 | 0.026116 | 0.104462 |
| フラッシュ | 3 | 413,870,908,056 | 0.020763 | 0.062289 |
| 真っ直ぐ | 2 | 1,142,885,476,800 | 0.057336 | 0.114671 |
| スリーオブアカインド | 1 | 5,325,911,611,716 | 0.267188 | 0.267188 |
| 何もない | 0 | 11,106,773,222,412 | 0.557199 | 0.000000 |
| 合計 | 19,933,230,517,200 | 1.000000 | 0.989038 |
エラーのコストは、イリノイ デュースの最適リターン (2 番目の表) から、NSUD 戦略を使用したイリノイ デュースのリターン (3 番目の表) を差し引いた値 = 0.989131 - 0.989038 = 0.000093 です。
Wizard of Vegasの記事で、リバーシブルロイヤルのリターンが105.22%だと読みました。このリターンは、カードの順番を含めた最適な戦略を前提としています。平均的なロイヤル勝利を前提とした場合のリターンはどれくらいでしょうか?また、基本ペイテーブルである通常の6-5ボーナスポーカー戦略を使った場合はどうでしょうか?
戦略の逸脱がないと仮定すると、60回中1回は連続ロイヤルとなります。リバーシブルロイヤルジャックポットは1回につき161,556の配当となります。その他のロイヤルは1回につき800の配当となります。したがって、ロイヤルの平均配当は(1/60)*161,556 + (59/60)*800 + 1回につき17,396となります。
すべてのロイヤルが 17,396 を支払うと仮定し、そのロイヤルの勝利に基づいて最適な戦略を実行すると、リターンは 103.56% に低下します。
基本ペイテーブルである標準的な 6-5 ボーナス ポーカー戦略をプレイすると、リターンはさらに 101.97% に低下します。
ビデオ ポーカーのプログラミングのヒントでは、ビデオ ポーカーでは 52 枚のカードのデッキで 2,598,960 通りのスターティング ハンドが存在するにもかかわらず、分析に必要なハンドのクラスは 134,459 種類だけであると説明しています。
質問なのですが、ジョーカーポーカーにはいくつのクラスがあるのでしょうか?
この問題について、私はビデオポーカーの数学の専門家である尊敬する同僚のゲイリー・ケーラーに尋ねました。ジョーカーの数に応じて、彼の答えは次のとおりです。
- ジョーカー1枚: 150,891
- ジョーカー2枚: 169,078
- ジョーカー3枚: 189,189
- ジョーカー4枚: 211,406
- ジョーカー5枚: 235,925
ビデオポーカーのプログラミングのヒントでは、ビデオポーカーでは52枚のカードデッキで2,598,960通りのスターティングハンドが存在するにもかかわらず、分析に必要なハンドの種類は134,459種類しかないと説明されています。質問なのですが、エースボーナスポーカーやシーケンシャルロイヤルでジャックポットを獲得できるゲームなど、カードの順番が重要なゲームをプレイする場合、分析に必要なハンドの種類はいくつになるのでしょうか?
この問題について、私はビデオポーカーの数学の専門家である尊敬する同僚、ゲイリー・ケーラーに尋ねました。彼の答えは15,019,680です。
ビデオポーカーでドロー後に保持されるカードの平均枚数はどれくらいですか?
以下の表は、10種類のゲームとペイテーブルにおける平均カード枚数を示しています。リストされているゲームの平均は2.05枚です。
ビデオポーカーで保持される平均カード
| ゲーム | ペイテーブル | 戻る | 平均カード保有数 |
|---|---|---|---|
| ボーナスデュース | 10-4-3-3 | 97.36% | 1.845550 |
| デュースワイルド | 25-15-9-5-3 | 100.76% | 1.926010 |
| ホワイトホットエース | 9-5 | 99.57% | 2.055630 |
| スーパーダブルダブルボーナス | 7-5 | 99.17% | 2.057280 |
| ダブルダブルボーナス | 9-5 | 97.87% | 2.058390 |
| トリプルダブルボーナス | 8-5 | 95.97% | 2.072620 |
| ボーナスポーカー | 8-5 | 99.17% | 2.080610 |
| ジャックス・オア・ベター | 9-5 | 98.45% | 2.081030 |
| ボーナスポーカーデラックス | 8-5 | 97.40% | 2.150470 |
| ダブルボーナス | 9-6-5 | 97.81% | 2.173550 |
マシンで1,200ドル以上勝った場合、小切手で支払われるオプションがあることは承知しています。とはいえ、仮に現金をカジノ発行の小切手に換金したいとします。9/6ジャックス・オア・ベターを25ドル(合計125ドル)の額面で完璧にプレイしたと仮定します。小切手に換金した場合、現金のうちどれくらいの損失が見込まれるでしょうか?
9-6ジャック・オア・ベターでは、フォー・オブ・ア・カインド以上のカードが揃うごとに1200ドル以上の勝利金が得られます。フルハウス以下の配当は0.911103です。現金がチェックに変わるか、ハウスエッジで失われるまで、元の資金を1/(1-0.911103) = 11.249016回使い切る必要があります。ハウスエッジは0.004561です。つまり、元の資金の0.004561 × 11.249016 = 0.051306倍の損失を被ると予想されます。
興味深いことに、9-6ダブルダブルボーナスでは、ハウスエッジが高いにもかかわらず、現金をチェックに交換するコストが低くなっています。このゲームでは、4種類のカード全てで勝率が高く、チェックの額も大きくなります。このゲームでは、フルハウス以下のリターンは0.777138です。つまり、チェックに交換するには、資金を1/(1-0.777138) = 4.487076回循環させる必要があります。9-6ダブルダブルボーナスのハウスエッジは0.010192です。したがって、現金に交換した場合の予想損失は4.487076 × 0.010192 = 0.045733となります。
4 種類以上をターゲットとする戦略の逸脱によってコストをさらに削減することもできますが、これは読者の課題として残しておきます。
この質問は、Wizard of Vegasの私のフォーラムで尋ねられ、議論されています。
マルチプレイ ビデオ ポーカーの 9/6 Jacks or Better でジャックポット (1,200 ドル以上の賞金) を獲得する確率はどれくらいですか?
もちろん、額面とプレイ回数によって異なります。以下の表にその確率を示します。
マルチプレイビデオポーカーにおけるジャックポットの確率
| 宗派 | 3 プレイ | 5 プレイ | 10 プレイ | 25 プレイ | 50 プレイ | 100プレイ |
|---|---|---|---|---|---|---|
| 0.01ドル | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000001 | 0.000001 |
| 0.05ドル | 0.000000 | 0.000000 | 0.000001 | 0.000001 | 0.000002 | 0.000022 |
| 0.10ドル | 0.000001 | 0.000001 | 0.000002 | 0.000006 | 0.000047 | 0.000378 |
| 0.25ドル | 0.000002 | 0.000003 | 0.000008 | 0.000053 | 0.000369 | 0.000556 |
| 0.50ドル | 0.000070 | 0.000115 | 0.000238 | 0.000782 | 0.001247 | 0.008527 |
| 1.00ドル | 0.000070 | 0.000128 | 0.000473 | 0.000786 | 0.009518 | 0.072671 |
| 2.00ドル | 0.000083 | 0.000363 | 0.000488 | 0.010002 | 0.070029 | 0.239753 |
| 5.00ドル | 0.000720 | 0.001290 | 0.012978 | 0.100374 | 0.318838 | 0.768839 |
| 25.00ドル | 0.041494 | 0.124818 | 0.348811 | 0.835708 | 0.995943 | 0.999983 |
この表は、ビデオ ポーカーの付録 2から抜粋したもので、大規模なシミュレーションでプレイヤーが各合計勝利を獲得する頻度を示しています。