このページ
スタック・エム・ハイ・ポーカー
概要
G2E で見かけ、現在はVideoPoker.comでプレイできるビデオ ポーカーのバリエーションの 1 つが Stack 'em High Poker です。
ゲームの主旨は、プレイヤーが賭け金を倍にしてこの機能を発動すると、2 枚または 3 枚のエースが配られた場合にドロー時に追加のハンドが得られ、配られた新しいエースがまだ配られていない残りのハンドに対して「スティッキー」になるという点です。
ルール
- ゲームは、3 プレイおよび 5 プレイのビデオ ポーカーのオプション機能です。
- フィーチャーを発動するには、プレイヤーは1ラインあたり10クレジットをプレイする必要があります。勝利は5クレジットのみに基づいて決定されます。プレイヤーに2枚または3枚のエースが配られた場合、ボーナスハンドが付与されます。ボーナスハンドの数には、プレイヤーが既に支払ったハンドも含まれます。
- ボーナスハンドの数はルールで公開されています。例えば、最もリベラルなボーナスポーカーでは、エースが2枚の場合は12、エースが3枚の場合は13のボーナスハンドが与えられます。
- プレイヤーが持っているハンドの数に関係なく、それらは垂直スタックの形になります。
- 交換カードは、スタックの一番下から順番に、一度に1ハンドずつ配られます。プレイヤーがドローで追加のエースを配られた場合、それらのエースは上位のハンドすべてでスティッキーになります。
- フィーチャーを発動するには、プレイヤーは配られた2枚または3枚のエースのみを持っている必要があります。他のカードを持っている場合、ボーナスハンドは獲得できません。
- ボーナス機能では、配られた 5 枚のカードと、以前のハンドから引かれた「スティッキー」エースが除かれた 52 枚のカードから、ドローのすべてのハンドが配られます。
- プレイヤーが賭け金を倍にしてフィーチャーを有効にすると、配当表が上昇することがよくあります。例えば、通常1~5コインの賭けで8-5のボーナスポーカーですが、プレイヤーがフィーチャーに賭け金を支払うと、配当表は10-7に上昇します。
例
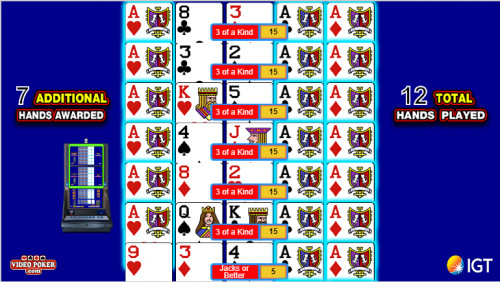
この画面では、ディールで2枚のエースを獲得し、それを保持していました。このスクリーンショットは、VideoPoker.comが誤ってフィーチャーをプレイしたプレイヤーにペイテーブルブーストを提供していなかったときに撮影されたものです。
次の画面には、最初の 5 つのボーナス ハンドが表示されていますが、いずれもエースのペアより上回るものではありません。
次の画面には、7つの追加ボーナスハンドが表示されています。下から2番目のハンドにはハートのエースが左の位置に配られていることに注目してください。このエースは、それより上のすべてのハンドに複製されています。しかし、どれもスリーカードより強いハンドではありませんでした。
リターンテーブル
以下の表は、私が知る限りの5人用Stack 'em Highのゲーム、ペイテーブル、スタックサイズ、リターンの一覧です。これらは入手可能な中で最も寛大なペイテーブルです。これより寛大でないペイテーブルも存在しますが、それがどのようなものかは分かりません。
積み重ねて高く -- 5 プレイ
| ゲーム | ペイテーブル | ボーナスゲーム* | 戻る |
|---|---|---|---|
| トリプルトリプルボーナス | 9-6 | 2,5 | 98.67% |
| ダブルダブルボーナス | 10-7-5 | 3,6 | 99.36% |
| トリプルダブルボーナス | 11-6 | 2,5 | 99.04% |
| ダブルボーナス | 11-7 | 4,8 | 99.10% |
| ボーナスポーカー | 10-7 | 7,8 | 99.42% |
| ホワイトホットエース | 9-6 | 3,4 | 99.19% |
| トリプルボーナス | 9-6 | 3,4 | 99.31% |
| スーパーダブルダブルボーナス | 8-5 | 3,2 | 99.55% |
| スーパーダブルボーナス | 9-6-5 | 4,8 | 99.44% |
| デュースワイルド | 16-14-4-4-3 | 3,8 | 99.24% |
| デュースワイルドボーナス | 11-4-3-3 | 3,6 | 98.21% |
| ルーズデュースワイルド | 17-13-4-3 | 1,2 | 99.11% |
| ダブルデュース | 16勝12敗 | 3,6 | 99.06% |
以下の表は、私が知る限りの3人用Stack 'em Highのゲーム、ペイテーブル、スタックサイズ、リターンの一覧です。これらは入手可能な中で最も寛大なペイテーブルです。これより寛大でないペイテーブルも存在しますが、それがどのようなものかは分かりません。
積み重ねて高く — 3プレイ
| ゲーム | ペイテーブル | ボーナスゲーム* | 戻る |
|---|---|---|---|
| トリプルトリプルボーナス | 9-6 | 3,2 | 99.35% |
| ダブルダブルボーナス | 10-8-6 | 3,5 | 99.14% |
| トリプルダブルボーナス | 9-7 | 3,2 | 99.28% |
| ダブルボーナス | 11-7-5 | 4,8 | 99.12% |
| ボーナスポーカー | 10-8-6 | 6,9 | 99.41% |
| ホワイトホットエース | 10-7-5 | 3,6 | 99.38% |
| トリプルボーナス | 10-7-5 | 3,6 | 99.51% |
| スーパーダブルダブルボーナス | 8-6-5 | 3,5 | 99.14% |
| スーパーダブルボーナス | 9-6-5 | 4,8 | 99.14% |
| デュースワイルド | 15-12-5-5-4 | 3,6 | 99.08% |
| デュースワイルドボーナス | 13-4-3-3 | 3,7 | 98.25% |
| ダブルボーナスデュースワイルド | 12-4-3 | 3,7 | 98.82% |
| ルーズデュースワイルド | 15-10-4-3 | 2,1 | 99.44% |
| ダブルデュース | 15-11-5 | 3,6 | 99.38% |
*: ボーナス ゲーム列の最初の数字には 2 つのエースの合計ゲーム数が表示され、2 番目の数字には 3 つのエースの合計ゲーム数が表示されます。
分析
以下は、5プレイ10-7ボーナスポーカーの分析です。ちなみに、このゲームではエースが2枚配られると12のボーナスハンド、エースが3枚配られると13のボーナスハンドが付与されます。プレイヤーがフィーチャーを発動すると、配当表が8-5から10-5にブーストされます。
次の表は、プレイヤーが 3 枚のシングルトンを捨てると仮定して、2 枚のエースが配られた後の 12 のボーナス ハンドのすべての可能な結果の確率を示しています。
2枚のエース(3枚のシングルトンを捨てた場合)のボーナスハンド確率
| 手 | 2枚のエース | ツーペア | スリーエース | フルハウス (エース2枚) | フルハウス (エース3枚) | 4枚のエース |
|---|---|---|---|---|---|---|
| 1 | 0.712858 | 0.159852 | 0.114339 | 0.002405 | 0.007771 | 0.002775 |
| 2 | 0.623834 | 0.139889 | 0.100059 | 0.002105 | 0.006800 | 0.002429 |
| 3 | 0.545927 | 0.122419 | 0.087564 | 0.001842 | 0.005951 | 0.002125 |
| 4 | 0.477749 | 0.107131 | 0.076628 | 0.001612 | 0.005208 | 0.001860 |
| 5 | 0.418085 | 0.093752 | 0.067059 | 0.001411 | 0.004557 | 0.001628 |
| 6 | 0.365873 | 0.082044 | 0.058684 | 0.001234 | 0.003988 | 0.001424 |
| 7 | 0.320181 | 0.071798 | 0.051355 | 0.001080 | 0.003490 | 0.001246 |
| 8 | 0.280196 | 0.062831 | 0.044942 | 0.000945 | 0.003054 | 0.001091 |
| 9 | 0.245204 | 0.054985 | 0.039329 | 0.000827 | 0.002673 | 0.000955 |
| 10 | 0.214582 | 0.048118 | 0.034418 | 0.000724 | 0.002339 | 0.000835 |
| 11 | 0.187784 | 0.042109 | 0.030119 | 0.000634 | 0.002047 | 0.000731 |
| 12 | 0.164332 | 0.036850 | 0.026358 | 0.000554 | 0.001791 | 0.000640 |
ボーナス終了までに、プレイヤーはハイペア4.556604個、ツーペア1.021777個、スリーカード4.917541個、フルハウス0.349576個、そしてフォーエース1.154503個の勝利を期待できます。エース2枚とシングルトン3枚を獲得した場合の平均ボーナス勝利額は、1×4.556604 + 2×1.021777 + 3×4.917541 + 10×0.349576 + 80×1.154503 = 117.208750となります。
次の表は、プレイヤーが別のペアとシングルトンを捨てると仮定して、2 枚のエースが配られた後の 12 のボーナス ハンドのすべての可能な結果の確率を示しています。
2枚のエース(ペアとシングルトンを捨てた場合)のボーナスハンド確率
| 手 | 2枚のエース | ツーペア | スリーエース | フルハウス (エース2枚) | フルハウス (エース3枚) | 4枚のエース |
|---|---|---|---|---|---|---|
| 1 | 0.710453 | 0.162134 | 0.114215 | 0.002529 | 0.007894 | 0.002775 |
| 2 | 0.621729 | 0.141886 | 0.099952 | 0.002213 | 0.006908 | 0.002429 |
| 3 | 0.544085 | 0.124167 | 0.087469 | 0.001936 | 0.006045 | 0.002125 |
| 4 | 0.476137 | 0.108660 | 0.076546 | 0.001695 | 0.005290 | 0.001860 |
| 5 | 0.416675 | 0.095090 | 0.066986 | 0.001483 | 0.004630 | 0.001628 |
| 6 | 0.364639 | 0.083215 | 0.058621 | 0.001298 | 0.004052 | 0.001424 |
| 7 | 0.319101 | 0.072823 | 0.051300 | 0.001136 | 0.003546 | 0.001246 |
| 8 | 0.279250 | 0.063728 | 0.044893 | 0.000994 | 0.003103 | 0.001091 |
| 9 | 0.244376 | 0.055770 | 0.039287 | 0.000870 | 0.002715 | 0.000955 |
| 10 | 0.213858 | 0.048805 | 0.034381 | 0.000761 | 0.002376 | 0.000835 |
| 11 | 0.187150 | 0.042710 | 0.030087 | 0.000666 | 0.002079 | 0.000731 |
| 12 | 0.163778 | 0.037376 | 0.026330 | 0.000583 | 0.001820 | 0.000640 |
ボーナス終了までに、プレイヤーはハイペア4.541230個、ツーペア1.036362個、スリーカード4.912236個、フルハウス0.355669個、そしてフォーエース1.154503個の勝利を期待できます。エース2枚とシングルトン3枚を獲得した場合の平均ボーナス勝利額は、1×4.541230 + 2×1.036362 + 3×4.912236 + 10×0.355669 + 80×1.154503 = 117.267565となります。
次の表は、プレイヤーがスリーオブカインドを捨てた場合を想定して、2 枚のエースが配られた後の 12 のボーナス ハンドのすべての可能な結果の確率を示しています。
2枚のエース(スリーカードを捨てた場合)のボーナスハンド確率
| 手 | 2枚のエース | ツーペア | スリーエース | フルハウス (エース2枚) | フルハウス (エース3枚) | 4枚のエース |
|---|---|---|---|---|---|---|
| 1 | 0.705520 | 0.166883 | 0.113969 | 0.002714 | 0.008141 | 0.002775 |
| 2 | 0.617411 | 0.146041 | 0.099736 | 0.002375 | 0.007124 | 0.002429 |
| 3 | 0.540306 | 0.127803 | 0.087280 | 0.002078 | 0.006234 | 0.002125 |
| 4 | 0.472830 | 0.111843 | 0.076380 | 0.001819 | 0.005456 | 0.001860 |
| 5 | 0.413781 | 0.097875 | 0.066842 | 0.001591 | 0.004774 | 0.001628 |
| 6 | 0.362106 | 0.085652 | 0.058494 | 0.001393 | 0.004178 | 0.001424 |
| 7 | 0.316885 | 0.074955 | 0.051189 | 0.001219 | 0.003656 | 0.001246 |
| 8 | 0.277311 | 0.065595 | 0.044796 | 0.001067 | 0.003200 | 0.001091 |
| 9 | 0.242679 | 0.057403 | 0.039202 | 0.000933 | 0.002800 | 0.000955 |
| 10 | 0.212372 | 0.050234 | 0.034306 | 0.000817 | 0.002450 | 0.000835 |
| 11 | 0.185850 | 0.043961 | 0.030022 | 0.000715 | 0.002144 | 0.000731 |
| 12 | 0.162641 | 0.038471 | 0.026273 | 0.000626 | 0.001877 | 0.000640 |
ボーナス終了までに、2枚のエースと捨て札のスリーカード1枚から始まり、プレイヤーはハイペア4.509694個、ツーペア1.066716個、スリーカード4.901626個、フルハウス0.367461個、フォーエース1.154503個の勝利を期待できます。2枚のエースと3枚のシングルトンカードを獲得した場合の平均ボーナス勝利額は、1×4.509694 + 2×1.066716 + 3×4.901626 + 10×0.367461 + 80×1.154503 = 117.2200063となります。
次の表は、プレイヤーが 2 枚のシングルトンを捨てると仮定して、3 枚のエースが配られた後の 13 のボーナス ハンドのすべての可能な結果の確率を示しています。
3枚のエース(2枚のシングルトンを捨てた場合)のボーナスハンド確率
| 手 | スリーエース | フルハウス | 4枚のエース |
|---|---|---|---|
| 1 | 0.896392 | 0.061055 | 0.042553 |
| 2 | 0.858248 | 0.058457 | 0.083296 |
| 3 | 0.821727 | 0.055969 | 0.122304 |
| 4 | 0.786760 | 0.053587 | 0.159653 |
| 5 | 0.753280 | 0.051307 | 0.195413 |
| 6 | 0.721226 | 0.049124 | 0.229650 |
| 7 | 0.690536 | 0.047033 | 0.262431 |
| 8 | 0.661151 | 0.045032 | 0.293817 |
| 9 | 0.633017 | 0.043116 | 0.323867 |
| 10 | 0.606080 | 0.041281 | 0.352639 |
| 11 | 0.580289 | 0.039524 | 0.380186 |
| 12 | 0.555596 | 0.037842 | 0.406561 |
| 13 | 0.531954 | 0.036232 | 0.431814 |
ボーナス終了までに、エース3枚とシングルトン2枚でスタートした場合、プレイヤーはスリーカードで9.096256回、フルハウスで0.619559回、エース4枚で3.284185回勝利すると予想されます。エース2枚とシングルトン3枚の場合の平均ボーナス勝利額は、3×9.096256 + 10×0.619559 + 80×3.284185 = 296.219154となります。
次の表は、プレイヤーがペアを捨てると仮定して、3 枚のエースが配られた後の 13 のボーナス ハンドのすべての可能な結果の確率を示しています。
3枚のエース(ペアを捨てた場合)のボーナスハンド確率
| 手 | スリーエース | フルハウス | 4枚のエース |
|---|---|---|---|
| 1 | 0.895467 | 0.061980 | 0.042553 |
| 2 | 0.857362 | 0.059342 | 0.083296 |
| 3 | 0.820879 | 0.056817 | 0.122304 |
| 4 | 0.785948 | 0.054399 | 0.159653 |
| 5 | 0.752503 | 0.052084 | 0.195413 |
| 6 | 0.720482 | 0.049868 | 0.229650 |
| 7 | 0.689823 | 0.047746 | 0.262431 |
| 8 | 0.660469 | 0.045714 | 0.293817 |
| 9 | 0.632364 | 0.043769 | 0.323867 |
| 10 | 0.605455 | 0.041906 | 0.352639 |
| 11 | 0.579691 | 0.040123 | 0.380186 |
| 12 | 0.555023 | 0.038416 | 0.406561 |
| 13 | 0.531405 | 0.036781 | 0.431814 |
ボーナス終了までに、エース3枚とペア1枚でスタートした場合、プレイヤーはスリーカードで9.086869回、エース4枚で0.619559回、0.628946回、そしてエース4枚で3.284185回勝利すると予想されます。エース2枚とシングルトン3枚の場合の平均ボーナス勝利額は、1×4.509694 + 2×1.066716 + 3×9.086869 + 10×0.628946 + 80×3.284185 = 296.2233478となります。
次の表は、10-5ボーナスポーカーで、プレイヤーが配られたカードにエースが0枚、1枚、または4枚ある場合のドロー後の期待リターンを示しています。右下のセルは、プレイヤーが配られたカードにエースが0枚、1枚、または4枚ある場合、94.53%のリターンが期待できることを示しています。
配られたカードにエースが0、1、または4枚ある10-7ボーナスポーカー
| 手 | 支払う | 組み合わせ | 確率 | 戻る |
|---|---|---|---|---|
| ロイヤルフラッシュ | 800 | 407,220,072 | 0.000021 | 0.017054 |
| ストレートフラッシュ | 50 | 2,165,260,068 | 0.000113 | 0.005667 |
| 4枚のエース | 80 | 6億6,473万9,580 | 0.000035 | 0.002784 |
| 4対2-4 | 40 | 10,499,553,552 | 0.000550 | 0.021985 |
| 5-K 4つ | 25 | 32,463,889,224 | 0.001699 | 0.042486 |
| フルハウス | 10 | 202,070,667,924 | 0.010578 | 0.105781 |
| フラッシュ | 7 | 290,934,586,020 | 0.015230 | 0.106610 |
| 真っ直ぐ | 4 | 217,043,262,036 | 0.011362 | 0.045448 |
| スリーオブアカインド | 3 | 1,363,205,170,488 | 0.071362 | 0.214086 |
| 2組 | 2 | 2,305,997,183,808 | 0.120716 | 0.241432 |
| ジャック以上 | 1 | 3,581,309,420,208 | 0.187477 | 0.187477 |
| 何もない | 0 | 11,095,933,632,060 | 0.580857 | 0.000000 |
| 合計 | 19,102,694,585,040 | 1.000000 | 0.990810 |
この10-7ボーナスポーカー分析の最終テーブルでは、ディールのハンドによってすべてがまとめられています。勝利は5ハンドのベットに基づいて表されます。リターンの列は、勝利、確率、そして0.1を掛け合わせたものです。10で割っているのは、プレイヤーは1ハンドにつき10コインをベットする必要があるためです。右下のセルは、ゲーム全体のリターンが99.42%であることを示しています。
10-7ボーナスポーカーリターン(フィーチャー付き)
| 取引 | 組み合わせ | 確率 | 平均勝利 | Exp. Win |
|---|---|---|---|---|
| 配られたエースが0、1、または4枚 | 2,490,672 | 0.958334 | 4.954049 | 0.474763 |
| 2枚のエースと3枚のシングルトンが配られる | 84,480 | 0.032505 | 117.208750 | 0.380991 |
| 2枚のエース、もう1枚のペア、そしてシングルトンが配られる | 19,008 | 0.007314 | 117.267565 | 0.085766 |
| 2枚のエースと3枚の同じカード | 288 | 0.000111 | 117.382829 | 0.001301 |
| 3枚のエースと2枚のシングルトンが配られる | 4,224 | 0.001625 | 296.219154 | 0.048143 |
| 3枚のエースと3枚のペアが配られる | 288 | 0.000111 | 296.284864 | 0.003283 |
| 合計 | 2,598,960 | 1.000000 | 0.994248 |
謝辞
VideoPoker.comの Web サイトのスクリーンショットとこのページに掲載されているリターン テーブルの使用を許可していただいたことに感謝いたします。